AP Syllabus focus:
‘Learning Objective VAR-5.A: Introduce the concept of a random variable as representing numerical outcomes of random behavior. Essential Knowledge VAR-5.A.1: Discuss what random variables are and VAR-5.A.2: Explain how discrete random variables can only assume a countable number of values, each with a specific probability, and that the sum of all these probabilities equals 1.’
Understanding random variables is essential in probability and statistics because they provide a structured way to assign numerical values to uncertain outcomes, enabling deeper analytical insight.
What Is a Random Variable?
A random variable is a foundational concept in probability that allows statisticians to translate outcomes of random processes into numerical values. This subsubtopic emphasizes that random variables represent the numerical outcomes of random behavior, directly aligning with Learning Objective VAR-5.A.
Random Variable: A variable that assigns a numerical value to each possible outcome of a random process.
A random variable does not describe the outcome itself but rather the number linked to the outcome. For example, instead of describing an outcome as “a heads appears,” a random variable might assign the value 1 to heads and 0 to tails. This transformation enables mathematical analysis, probability calculations, and comparison across scenarios. Random variables make it possible to quantify uncertainty and describe patterns within chance processes.
Random variables are typically introduced in probability models that involve repeated trials, random selections, or unpredictable events.
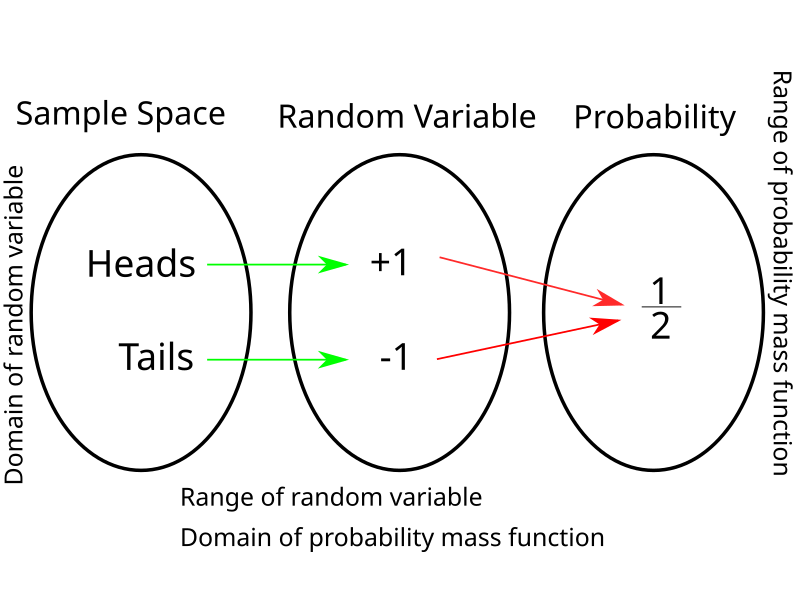
This diagram illustrates a random variable as a function mapping outcomes to numerical values, alongside a discrete probability function that reflects how each value receives an associated probability. Source.
Discrete Random Variables
This section focuses specifically on discrete random variables, as described in Essential Knowledge VAR-5.A.2. These random variables take on a countable set of possible values, rather than any value within an interval.
Discrete Random Variable: A random variable that can assume only a countable number of distinct values, each occurring with an associated probability.
Discrete random variables commonly arise in processes where outcomes naturally fall into separated numerical categories. Because the values are countable, such variables are often listed in tables, graphs, or enumerated sets. Each value of a discrete random variable corresponds to a probability that it occurs, reflecting the likelihood of that value under the random process being studied.
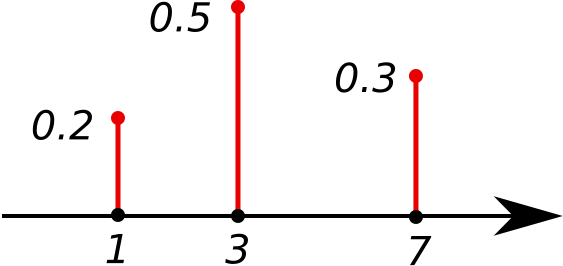
This bar graph depicts a discrete probability mass function, demonstrating how each possible value of a discrete random variable has a specific probability and how these probabilities form a complete distribution. Source.
Unlike continuous random variables, which can take infinitely many values in an interval, discrete random variables contain fixed, isolated points—such as 0, 1, 2, or any other countable sequence.
Probabilities Associated with Discrete Random Variables
A defining feature of discrete random variables is the assignment of a specific probability to each possible value. Essential Knowledge VAR-5.A.2 requires students to understand that these probabilities must follow strict mathematical rules that preserve logical consistency and reflect real-world likelihoods.
Each value has a probability between 0 and 1, and higher probabilities indicate more likely outcomes. Because these values represent all possible outcomes of a random process, the probabilities must collectively describe the complete behavior of that process.
EQUATION
= Probability of the discrete random variable taking value
This relationship ensures that the list of probabilities accounts for every possible outcome. It reinforces that probabilities are not arbitrary; they must collectively sum to 1 to form a valid probability distribution.
This rule also implies that if even one potential value is missing or incorrectly assigned, the probability model becomes invalid. Therefore, defining the full set of values and their probabilities is critical when working with discrete random variables.
Representing Numerical Outcomes of Random Behavior
A random variable does not alter the randomness of a process—it simply captures randomness numerically. This conversion is fundamental to all later statistical topics, including probability distributions, expected value, and inference procedures.
To connect outcomes of random processes with numerical values, students must recognize that:
A random process produces unpredictable outcomes.
A random variable assigns numbers to these outcomes.
The assigned numbers allow outcomes to be organized, analyzed, and compared.
Because the numerical values correspond directly to possible outcomes, understanding the relationship between the underlying process and the random variable's values is essential. For example, the random variable might represent:
Counts, such as the number of successes in repeated trials.
Indicators, such as 0 or 1 to represent failure or success.
Categorical assignments, such as assigning values to types of outcomes.
These assignments allow probability models to be applied systematically.

This bar chart shows the discrete probability distribution for a fair six-sided die, illustrating how random variables can numerically represent real-world random behavior with equal probabilities assigned to each outcome. Source.
Why Random Variables Matter in Statistics
Random variables provide the quantitative foundation for almost every major concept in AP Statistics. They allow probabilities to be computed, distributions to be compared, and uncertainty to be measured. By turning qualitative outcomes into numerical values, random variables help connect real-world randomness to mathematical models.
Discrete random variables, in particular, are central to many statistical applications, including simulations, probability distributions, and models used in inference. Their properties—specifically a countable set of values and associated probabilities that sum to 1—make them well-suited for constructing probability distributions that accurately describe patterns of variability in random processes.
FAQ
A random variable translates outcomes into numerical form, while the outcomes themselves might be words, categories, or physical results.
The random variable creates a consistent numerical framework that allows probabilities to be computed, distributions to be constructed, and comparisons to be made.
It is not the outcome but the numerical representation of that outcome that becomes the basis for analysis.
Yes. A discrete random variable may take negative values if the context of the random process logically allows it.
Common examples include:
• Net gain or loss in a game or transaction
• Temperature changes represented as deviations from a baseline
• Integer-valued differences between two measured quantities
What matters is that the values remain countable and relevant to the scenario.
Discrete models simplify complex behaviour by focusing on the outcomes most relevant to the question being analysed.
They are particularly useful when:
• Outcomes naturally occur in whole numbers
• Only certain categories or counts matter
• Precision beyond integers adds little value
This simplification often makes probability calculations more accessible while still capturing essential patterns of variation.
A numerical assignment is valid if it maps each outcome to a unique number and preserves the structure of the random process.
Assignments should be:
• Consistent across trials
• Meaningful for interpretation
• Suitable for calculating probabilities and summarising behaviour
Arbitrary or inconsistent mappings can distort analysis and make comparisons misleading.
A complete set includes every numerical value the random variable can legitimately take, with none omitted.
Completeness ensures:
• Probabilities account for all outcomes
• The distribution reflects the entire random process
• No probability mass is unassigned or duplicated
If even one possible value is missing, the distribution cannot be considered valid.
Practice Questions
A random variable is used to represent the number of pets owned by a randomly selected household. Explain why this variable is considered a discrete random variable.
(1–3 marks)
• Award 1 mark for stating that the number of pets is a numerical outcome of a random process (selecting a household).
• Award 1 mark for stating that the values are countable whole numbers (0, 1, 2, …).
• Award 1 mark for stating that no values between whole numbers are possible, hence it is discrete.
(Max 3 marks)
A random process involves observing the number of customers who enter a shop during a one-hour period. Let X be the random variable representing this number.
(a) Define a random variable in the context of this scenario.
(b) Give two possible values that X may take and briefly explain why each value corresponds to a probability.
(c) Explain why the probabilities of all possible values of X must sum to 1.
(4–6 marks)
(a)
• Award 1 mark for stating that a random variable assigns numerical values to outcomes of a random process.
• Award 1 mark for relating this specifically to the number of customers entering the shop.
(2 marks)
(b)
• Award 1 mark for any two plausible values (e.g., 0 and 12).
• Award 1 mark for explaining that each value has an associated probability because it represents a possible outcome of the random process.
(2 marks)
(c)
• Award 1 mark for stating that the probabilities must sum to 1 because they represent all possible outcomes.
• Award 1 mark for explaining that the collection of probabilities must include every value that X can take.
(2 marks)
(Max 6 marks)

