Understanding how to interpret a sampling distribution for sample means is essential for linking statistical theory to real-world reasoning, allowing students to make justified claims about population characteristics.

Interpreting Sampling Distributions for Sample Means

A sampling distribution for a sample mean describes the behavior of the sample mean across all possible random samples of the same size from a population. Interpreting this distribution correctly allows us to connect sample-level information to population-level conclusions, which is a central goal of statistical inference. The AP specification emphasizes interpretation using correct units, appropriate context, and understanding the implications of the distribution’s mean and standard deviation.

Understanding Parameters in Context

When working with sampling distributions, the two parameters that guide interpretation are the mean of the sampling distribution and the standard deviation of the sampling distribution. These parameters describe how sample means behave, not how individual data values behave, which is a distinction students must consistently maintain.

Because the sampling distribution mean equals the population mean, interpreting it requires stating the connection explicitly in context. For example, if a population mean represents a typical measurement, then the sampling distribution mean represents the long-run average of sample means for that same measurement. The unit of measurement always matches the population variable.

Standard Deviation and Variability of Sample Means

The standard deviation of the sampling distribution communicates how much the sample means vary from sample to sample. Its role is to describe the expected spread of sample means rather than the spread of individual observations.

EQUATION

This equation highlights that increasing the sample size reduces the variability of the sample mean, which strengthens the precision of inferences. When interpreting this parameter, students should focus on what it tells them about the expected closeness of sample means to the population mean.

The sampling distribution of x̄ has mean equal to the population mean and standard deviation equal to the standard error, so larger samples produce less variable sample means.

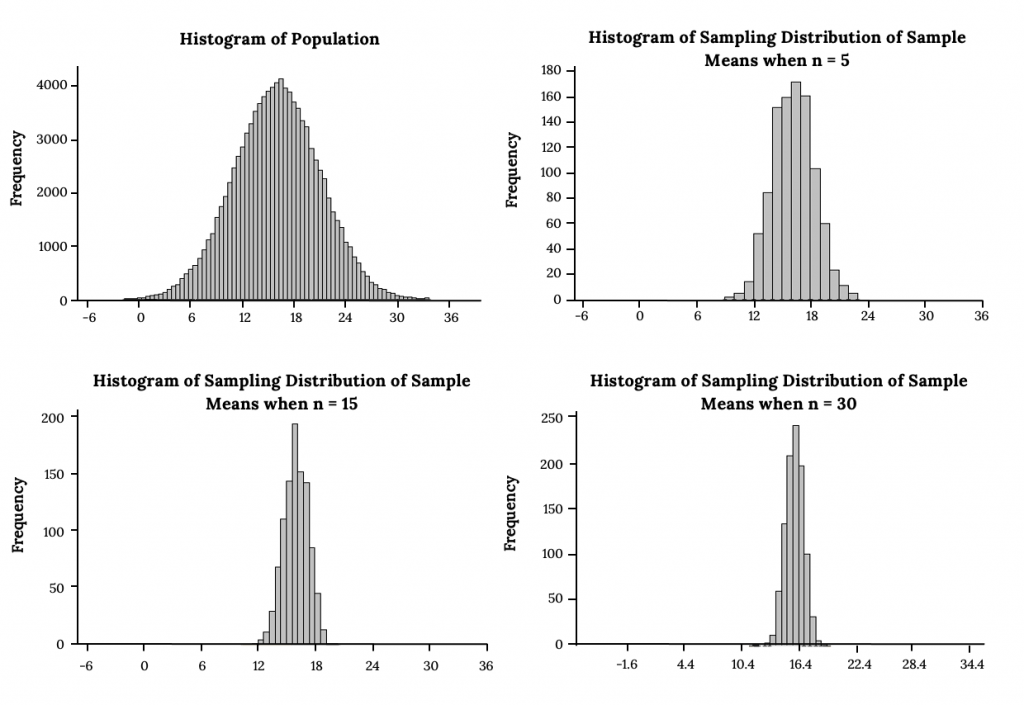
This figure compares the population distribution with sampling distributions of the sample mean for different sample sizes. Each distribution of x̄ remains centered at the population mean but narrows as n increases, illustrating how the standard error decreases. It visually reinforces how sample means become more consistent as sample size grows. Source.

Using Appropriate Units in Interpretation

Units play a vital role in interpretation. Each statistic, parameter, or distributional value must be expressed in the same units as the underlying numerical variable. Without proper units, statements lose meaning, especially when comparing statistics or making probability claims. Units should always match the context of the study, such as grams, hours, dollars, or centimeters.

Interpreting Probabilities from a Sampling Distribution

Probabilities in a sampling distribution describe the likelihood of obtaining a sample mean in a particular range when repeatedly sampling from the population. These probabilities do not refer to individual data points; instead, they express the behavior of the sample mean across samples.

When interpreting probabilities, students should:

• Identify clearly that the probability relates to the sample mean $\bar{x}$, not individual observations.

• Connect probability statements to the defined context of the population and sampling process.

• Use correct units for any bounds or values referenced in the probability statement.

• Phrase interpretations in terms of long-run relative frequency of sample means.

When the sampling distribution of x̄ is approximately normal, probabilities about the sample mean are interpreted as areas under the normal curve, measured in standard-error units.

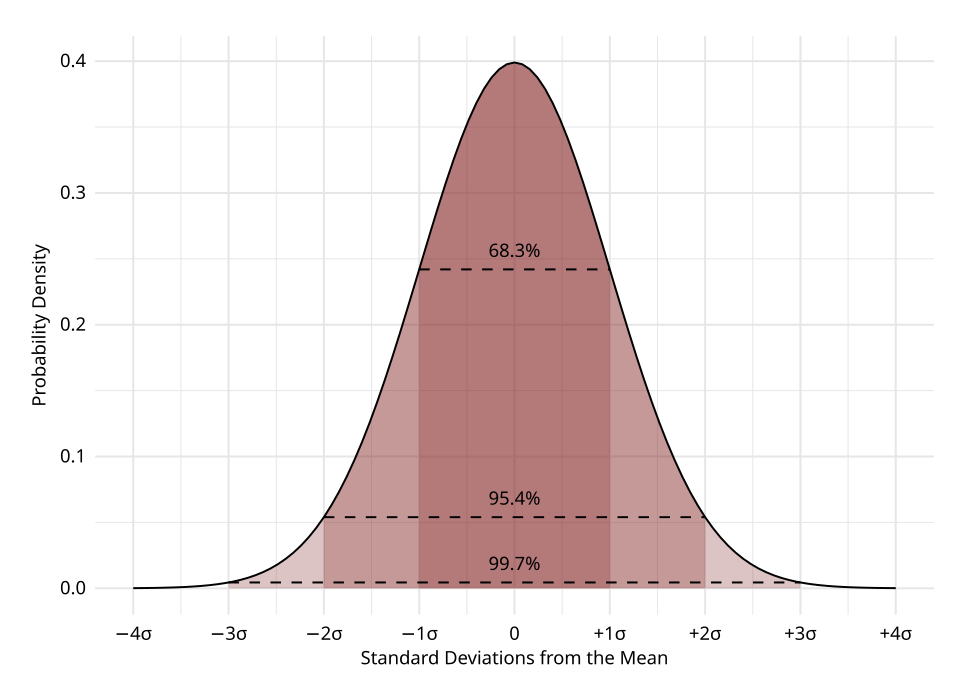
This standard normal curve shows the proportion of values within one, two, and three standard deviations of the mean. When applied to sampling distributions, these shaded areas represent the likelihood that the sample mean falls within corresponding numbers of standard errors. The 68–95–99.7 pattern provides a visual basis for interpreting normal probabilities. Source.

Role of Context in Interpretation

Context anchors all interpretation. A sampling distribution cannot be interpreted meaningfully without identifying:

• The population being studied.

• The variable measured.

• The sample size used.

• The unit associated with the measurement.

When interpreting the parameters or probabilities, students should restate these contextual details to show understanding of how the sampling distribution connects to the real situation. For instance, instead of stating that “the mean equals 50,” the interpretation should say that “the mean of the sampling distribution of the sample mean is 50 units, representing the long-run average of sample means for this population.”

Implications for Inference About the Population Mean

Interpreting a sampling distribution involves understanding how its parameters inform conclusions about the population mean. Key implications include:

• A smaller standard deviation of the sampling distribution indicates more consistent sample means, strengthening confidence in estimates.

• The equality of the sampling distribution mean and the population mean validates using $\bar{x}$ as an unbiased estimator.

• Knowledge of the distribution’s spread helps determine how unusual or typical a particular sample mean is.

• Probability interpretations allow students to quantify how likely certain sample means are, which supports formal inference procedures.

Key Interpretive Practices for AP Statistics

To interpret sampling distributions effectively, students should use the following practices:

• State all results with units that match the original variable.

• Link every interpretation to the population context, not just the sample.

• Emphasize the behavior of sample means, making clear distinctions from individual observations.

• Use precise language, such as “in repeated random sampling,” to reflect the conceptual foundation of sampling distributions.

• Interpret parameters before probabilities, ensuring understanding of the distribution’s structure before analyzing events within it.