The margin of error quantifies expected sampling variability when estimating a population proportion. It uses the critical value and standard error to construct an interval estimate.

Computing the Margin of Error

The margin of error is a central idea in constructing a one-sample confidence interval for a population proportion. It measures how far the sample proportion $,\hat p,$ might reasonably fall from the true population proportion, assuming proper conditions for inference are met. This subsubtopic focuses specifically on how to compute the margin of error once the standard error has been established and the confidence level has been chosen. Because the margin of error incorporates both sampling variability and the level of certainty desired, understanding its components strengthens a student’s ability to make sound statistical inferences.

The Role of Sampling Variability

The margin of error reflects the expected variation in $\hat p$ from sample to sample. This variation arises because each random sample may include slightly different outcomes, even when drawn from the same population. The margin of error formalizes this variability by combining the estimated spread of the sampling distribution with the critical value, which indicates the degree of confidence required.

Key Components of the Computation

Two quantities must be available before the margin of error can be computed:

• Sample proportion $\hat p$, which serves as the point estimate.

• Critical value $z^*$, obtained from the standard normal distribution and associated with a selected confidence level.

A third component, the standard error, provides the estimated standard deviation of the sampling distribution of $\hat p$. Although computed in a previous step of the interval procedure, it remains essential in determining the margin of error for a population proportion.

Definition of the Margin of Error

After defining the concept, it is important to note that the magnitude of the margin of error depends on both the confidence level and the amount of variability present in the sample data.

Formula for the Margin of Error

The formula used in this subsubtopic stems directly from the combination of the critical value and the standard error of the sample proportion.

EQUATION

This equation shows that the margin of error is scaled by the level of confidence (through $z^*$) and shaped by the sample’s estimated variability (through $\hat p$ and $n$).

A sentence is required between equation blocks, and this one explains that the equation links theoretical distributional properties with practical sample information, ensuring proper interpretation.

For a chosen confidence level C, the critical value $z^*$ comes from the standard normal distribution and tells us how many standard errors to move away from the center.

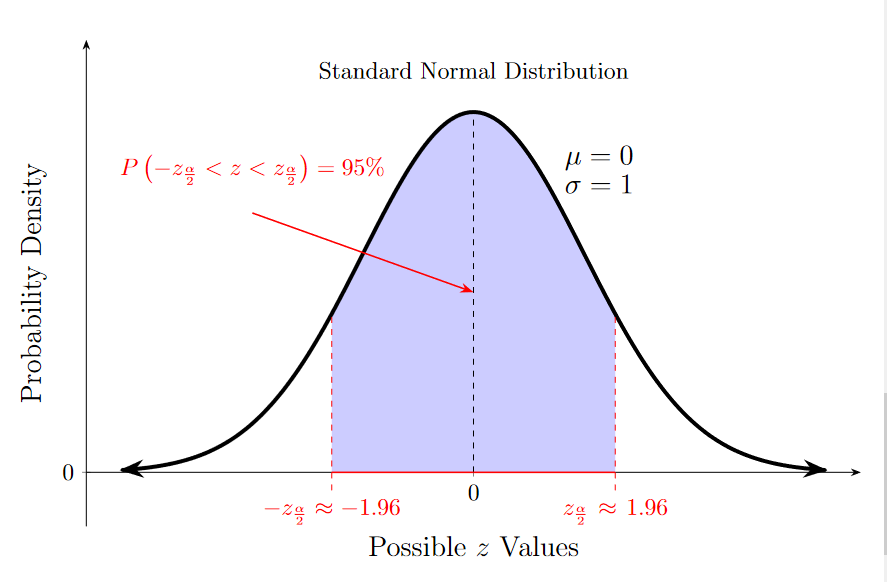
The standard normal curve shows the central 95% of z-scores between −1.96 and 1.96, illustrating how confidence levels determine the critical value used in margin-of-error calculations. Source.

How the Formula Reflects Sampling Behavior

Because the expression $\sqrt{\hat p(1-\hat p)/n}$ models the estimated spread of all possible sample proportions, multiplying it by the critical value broadens or narrows the range around $\hat p$ based on how confident the analyst wants to be. Larger critical values create wider margins of error, signifying the need for more certainty. Smaller critical values reduce the margin, indicating more tolerance for uncertainty.

Factors That Change the Margin of Error

When analyzing how the margin of error behaves, consider how each component contributes:

• Confidence level:

  • Higher levels (e.g., 99%) increase $z^*$, producing a larger margin of error.

  • Lower levels (e.g., 90%) decrease $z^*$, producing a smaller one.

• Sample size ($n$):

  • A larger sample size reduces the standard error and therefore reduces the margin of error.

  • A smaller sample size increases the standard error, widening the margin.

• Sample proportion ($\hat p$):

  • When $\hat p$ is near 0.5, variability is largest, resulting in a wider margin.

  • When $\hat p$ is near 0 or 1, variability is smaller, narrowing the margin.

Interpreting the Margin of Error

The margin of error expresses the radius of the confidence interval centered at $\hat p$. It represents how much the sample proportion might reasonably differ from the true population proportion due to random sampling error. Because it directly influences the width of the interval, understanding the margin of error is essential for evaluating the precision of an estimate.

The margin of error describes how far we expect the sample proportion $\hat p$ to fall from the true population proportion p when the normal model for the sampling distribution is appropriate.

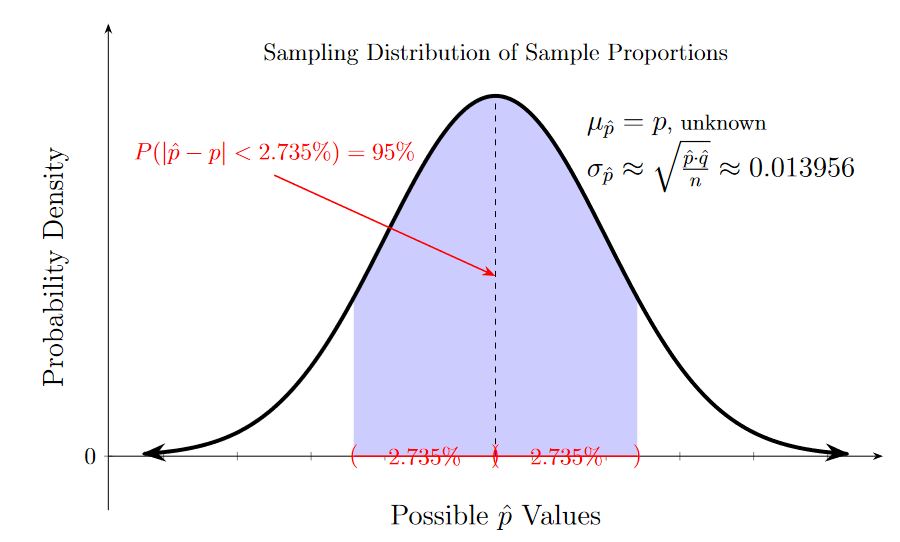
The sampling distribution diagram highlights the central region around the true proportion, showing how the margin of error bounds the range of typical sample proportions. Source.

Process Summary for Computing the Margin of Error

• Identify the sample proportion $\hat p$.

• Confirm the confidence level and determine $z^*$ from the standard normal distribution.

• Calculate the standard error $\sqrt{\hat p(1-\hat p)/n}$.

• Multiply the critical value and the standard error to obtain the margin of error.

• Use the margin of error in constructing a confidence interval for a population proportion.

Increasing the confidence level (and therefore using a larger $z^*$) makes the margin of error larger, while increasing the sample size n makes the margin of error smaller.

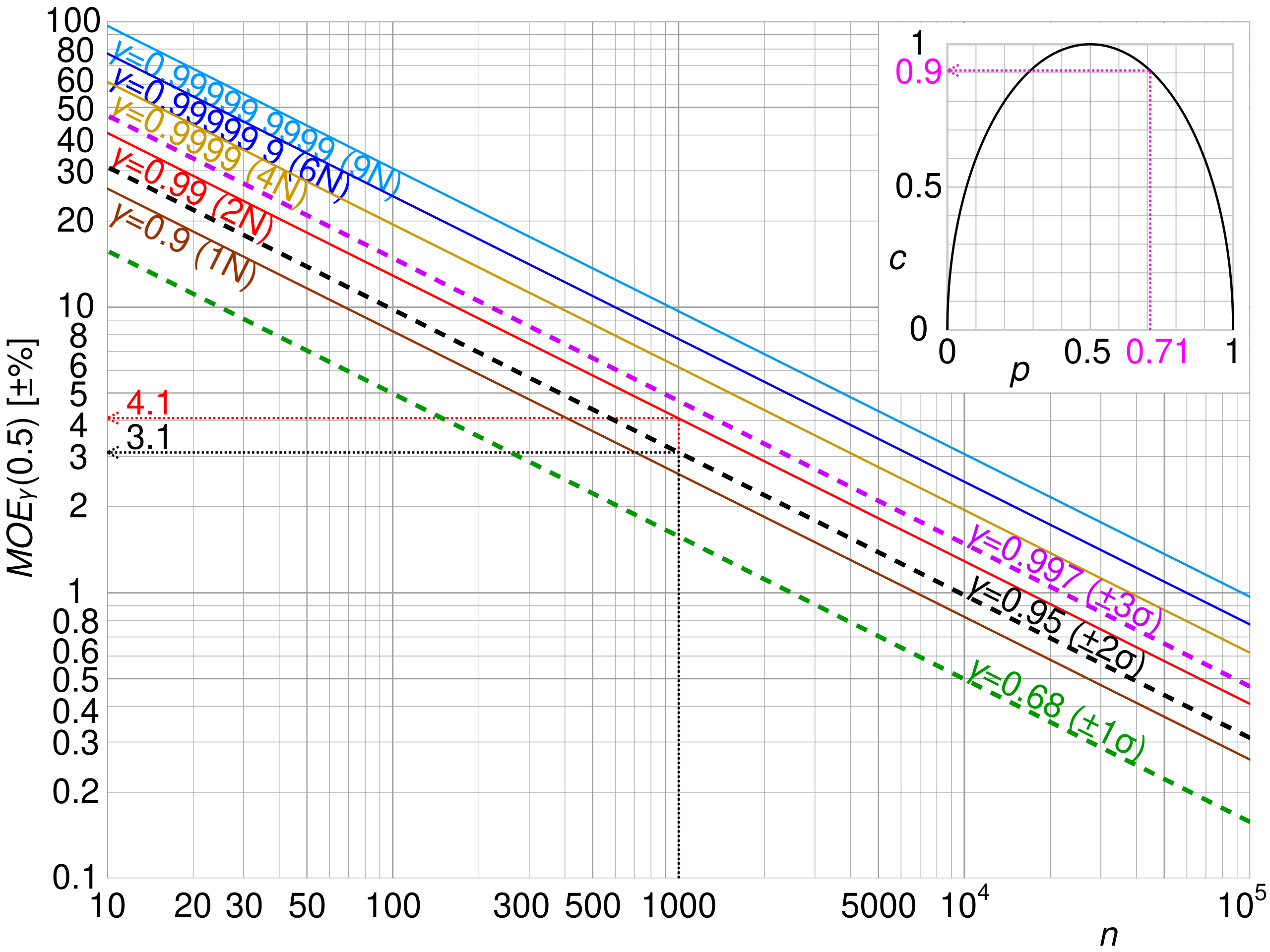
This multi-curve plot shows how the margin of error decreases with larger sample sizes and increases with higher confidence levels, reinforcing the relationship described in the text. Source.