AP Syllabus focus:
‘Independence: Ensure data is collected via a random sample or experiment, and if sampling without replacement, the sample size should not exceed 10% of the population. Large Counts: All expected counts should be greater than 5 to ensure the accuracy of the chi-square test. This requirement helps to mitigate the effects of small sample sizes that could otherwise distort the chi-square statistic’s distribution, ensuring the test's validity.’
To use a chi-square goodness-of-fit test reliably, students must verify specific conditions that ensure the test statistic follows a chi-square distribution closely enough for sound inference.
Verifying Conditions for Chi-Square Goodness of Fit
This subsubtopic focuses on confirming that the data structure and sampling process justify applying a chi-square goodness-of-fit test, which evaluates how well observed categorical counts match expected counts under a stated null distribution.
Independence Condition
The independence condition ensures that each observational unit contributes one categorical outcome and that outcomes do not influence one another. This requirement supports the mathematical assumptions behind the chi-square distribution.
Independence: A condition stating that individual observations must not affect one another; each contributes uniquely and separately to the categorical data collected.
To confirm independence in applied settings, the data should come from a random sample or randomized experiment, because randomness supports the assumption that the responses behave independently in the population.
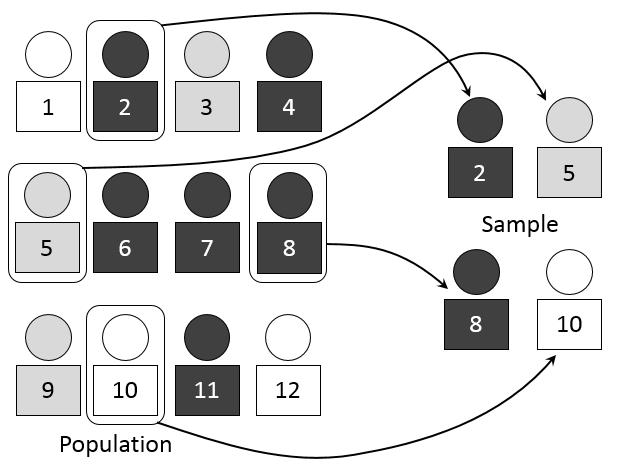
This diagram shows a larger population and a smaller subset selected as a simple random sample. Each element in the population has an equal chance of being chosen, illustrating independence of observations. The image focuses only on the core idea of random sampling and does not introduce additional statistical concepts beyond those discussed in this subsubtopic. Source.
A random sampling method or random assignment helps justify treating the sample as representative, but students must still verify that the sample’s size relative to the population does not violate independence. These requirements protect the test from inflating or deflating the chi-square statistic due to structural dependence.
Using the 10% Condition
When data are collected without replacement, sampling a large fraction of the population produces observations that become increasingly related to one another. To guard against this issue:
Confirm that the sampling method is without replacement.
Determine the approximate population size relevant to the categorical variable.
Verify that the sample size is no more than 10% of the population.
If the sample exceeds this threshold, independence may not hold, and a chi-square test may not be appropriate.
These steps ensure observational independence, which is essential for the chi-square approximation to apply.
Large Counts Condition
The large counts condition requires that all expected counts—not the observed counts—are sufficiently large. This ensures the chi-square test statistic behaves like the chi-square distribution predicted by theory.
Expected Count: The theoretical count for each category, computed under the assumption that the null hypothesis is true and used to compare against observed values.
Expected counts reflect what the distribution of outcomes should look like if the null hypothesis is accurate. If these values are too small, the resulting chi-square statistic may not follow a chi-square distribution closely, undermining the reliability of p-values.
Why Expected Counts Must Exceed 5
The commonly taught and syllabus-aligned guideline is that all expected counts must be greater than 5. This threshold is crucial because:
Small expected counts make the chi-square approximation unstable.
The test statistic may become overly sensitive or insufficiently sensitive to deviations from expectation.
The p-value may become inaccurate, leading to incorrect conclusions.
Larger expected counts create smoother distributions that align well with the theoretical chi-square curve.
This condition must be verified before computation of the chi-square statistic, ensuring validity for the inferential conclusions that follow.
Calculating Expected Counts to Check the Condition
The expected counts for each category are found by multiplying the sample size by the null proportion for that category.
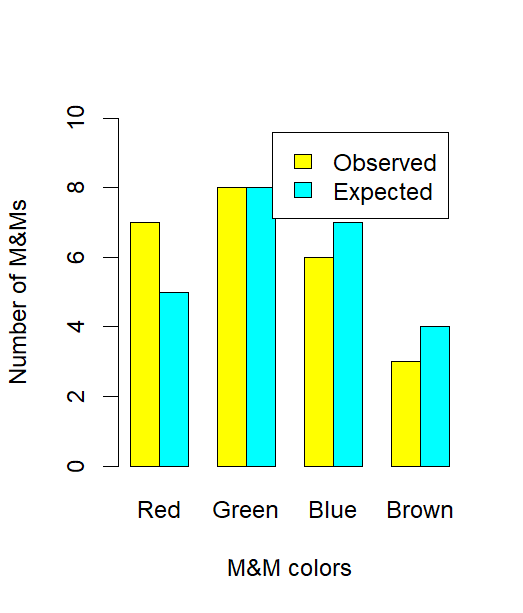
This bar chart displays expected and observed counts for several categories in a chi-square goodness-of-fit context. It illustrates how expected counts provide a benchmark for judging whether observed frequencies deviate substantially from what the null hypothesis predicts. The M&M context shown is extra detail not required by the syllabus but serves as a concrete visualization of comparing observed and expected values. Source.
EQUATION
= total sample size
= hypothesized proportion for category
Always compute all expected counts before proceeding with any test steps. If any expected count is 5 or below, adjustments such as combining categories or choosing a different inferential method may be necessary.
Integrating Both Conditions Before Testing
Verifying conditions is not a formality; it is a foundational step in categorical data inference. Students should check the independence and large counts conditions before computing the chi-square statistic because these conditions collectively justify using the chi-square distribution for p-value determination. Only when both conditions are satisfied can the chi-square goodness-of-fit test be applied confidently.
Checklist for Students
Independence:
Data come from a random sample or randomized experiment.
If sampling without replacement, sample ≤ 10% of population.
Large Counts:
Compute all expected counts.
Each expected count > 5 to maintain chi-square approximation accuracy.
These structured checks ensure that the test results meaningfully reflect differences between observed and expected categorical distributions and meet the syllabus standards for valid statistical inference.
FAQ
The chi-square distribution models the behaviour of sums of squared standardised deviations, which assumes reasonably smooth underlying probabilities. When expected counts are small, these deviations become erratic rather than smooth.
This leads to inaccurate p-values because the sampling distribution of the test statistic becomes skewed or overly discrete. As a result, the test may falsely detect significance or fail to detect it when appropriate.
Yes. The large counts condition refers only to expected counts, not observed ones. Low observed counts do not violate the condition.
However, very low observed values may increase sensitivity to outliers or misclassification errors. This is a practical, not theoretical, concern and does not affect the formal requirement for applying the test.
Categories may be merged when individual expected counts fall below 5, provided the combined category remains meaningful.
Limitations include:
Loss of detail about the distribution
Reduced interpretability of results
Risk of masking patterns present in the original categories
Combining must be done before looking at observed data-based conclusions to avoid post hoc bias.
Without replacement, each selected unit slightly changes the composition of the remaining population. This creates dependency between selections.
The 10% condition ensures that this dependency remains negligible. When the sample is small relative to the population, the probability of selecting any particular category remains effectively constant across draws.
Both require independent observational units, but the justification differs.
In observational studies, independence relies on a random sampling method.
In experiments, independence arises from random assignment, which ensures responses are not systematically related to pre-existing factors.
In both cases, failure of independence compromises the chi-square distribution’s validity.
Practice Questions
Question 1 (1–3 marks)
A researcher collects data from a simple random sample of 120 customers to perform a chi-square goodness-of-fit test on their preferred product category. The expected counts for all categories are above 5.
(a) State whether the conditions for using a chi-square goodness-of-fit test are satisfied, giving a brief justification.
Question 1
(a) Up to 3 marks:
1 mark: States that the independence condition is satisfied (because a simple random sample was used).
1 mark: States that the large counts condition is satisfied (all expected counts exceed 5).
1 mark: Concludes correctly that the chi-square test conditions are met.
Question 2 (4–6 marks)
A school surveys 95 students, drawn without replacement from a population of 1,400 students, to investigate whether the distribution of favourite sports matches a claimed distribution. The expected counts calculated under the null hypothesis for one category is 3.8, while all other expected counts exceed 5.
(a) Assess whether the independence condition is met.
(b) Explain whether the large counts condition is satisfied.
(c) State whether it is appropriate to proceed with a chi-square goodness-of-fit test and justify your reasoning.
Question 2
(a) Up to 2 marks:
1 mark: Recognises that sampling without replacement requires checking the 10% condition.
1 mark: Correctly states that 95 is less than 10% of 1,400, so independence is satisfied.
(b) Up to 2 marks:
1 mark: States that expected counts must all exceed 5 for the condition to hold.
1 mark: Identifies that because one expected count is 3.8, the large counts condition is not satisfied.
(c) Up to 2 marks:
1 mark: Concludes that a chi-square goodness-of-fit test is not appropriate.
1 mark: Provides a correct justification, such as the violation of the large counts condition meaning the chi-square approximation may not be reliable.

