The margin of error for a regression slope quantifies uncertainty in estimating the population slope, helping students understand how sample variability affects confidence when interpreting linear relationships.

Understanding Margin of Error in Regression Slope Inference

The margin of error for the slope describes how far the estimated slope of a sample regression line may reasonably vary from the true population slope. Because the slope is derived from sample data, it is subject to natural sampling variation, and the margin of error provides a structured way to express this uncertainty within a confidence interval. Students should recognize that the margin of error depends on both the critical t value and the standard error of the slope, each playing a distinct role grounded in statistical reasoning.

Components of the Margin of Error

Two key elements determine the size of the margin of error:

• The critical t value, reflecting the desired confidence level and degrees of freedom.

• The standard error of the slope, capturing how much slope estimates fluctuate across repeated samples.

Understanding these components is essential for accurate interpretation of interval estimates.

The Standard Error of the Slope

The standard error of the slope is a measure of the expected variability in the slope estimate when sampling from the same population repeatedly. Because different samples produce different regression lines, the standard error summarizes this variation numerically and influences the precision of the interval.

The standard error incorporates the variability of the response variable, the spread of the explanatory variable, and the sample size. Larger sample sizes reduce this standard error, meaning estimates become more stable across samples.

EQUATION

The formula demonstrates that increasing the sample size decreases the denominator, reducing the standard error and narrowing the margin of error.

A crucial idea is that the standard error reflects not just measurement variation but the underlying randomness of sampling. Students should be attentive to this conceptual link because it underpins both estimation and hypothesis testing.

The Critical t Value

The critical t value identifies the number of standard errors needed to capture the desired confidence level. It comes from the t distribution with $n - 2$ degrees of freedom, appropriate for simple linear regression. As confidence levels increase, the critical value increases, widening the margin of error to reflect greater certainty requirements.

Between this definition and its use in the formula, students should appreciate the balancing act between certainty and precision.

Sentence identified for Image 2 insertion:
The critical value $t^</em>$ comes from a t-distribution with $n - 2$ degrees of freedom and marks how far out into the tails we must go to capture the desired confidence level.*

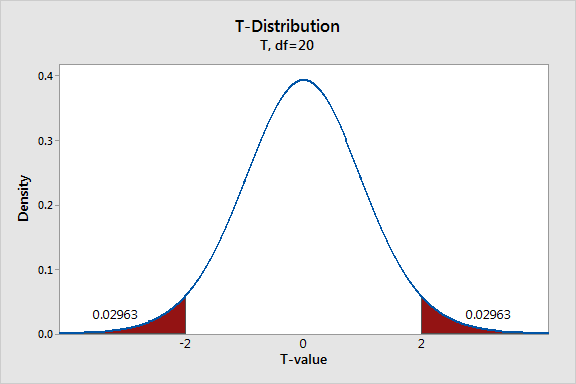
A t-distribution curve with shaded regions showing extreme t-values. The shaded tails represent how the critical value $t^</em>$ defines cutoff points needed to achieve a desired confidence level in slope estimation.* Source.

How the Margin of Error Is Formed

The margin of error combines the standard error of the slope and the critical t value. This combination indicates how far, in either direction, the estimated slope may reasonably fall from the true population slope under repeated sampling.

EQUATION

$ME = t^* \times SE_b$
$ME$ = Margin of error for the slope
$t^*$ = Critical t value for confidence level
$SE_b$ = Standard error of the slope

Because the margin of error is part of the confidence interval expression, its magnitude directly affects the width of the interval. Recognizing this connection helps students interpret the practical implications of the margin of error when evaluating linear relationships.

Factors Influencing the Margin of Error

Several features of the data and chosen confidence level influence the final margin of error:

• Sample size: Larger samples decrease the standard error, reducing the margin of error.

• Variability in residuals: Greater residual spread increases the standard error, enlarging the margin.

• Spread of x-values: A wider distribution of x-values typically produces a smaller standard error.

• Confidence level: Higher confidence requires a larger critical t value.

These factors align with the syllabus emphasis on understanding the role of variability. Students should be able to articulate how each factor affects the margin of error and why these changes matter in applied contexts.

Why the Margin of Error Matters

The margin of error serves as an essential component of statistical inference because it quantifies uncertainty in slope estimates. By connecting observed sample data to the unknown population slope, it provides structured guidance for interpreting the strength and direction of linear relationships.

Sentence identified for Image 3 insertion:
Because the margin of error multiplies the standard error of the slope, larger or smaller values of $SE_b$ lead to wider or narrower bands of plausible regression lines that are consistent with the data.

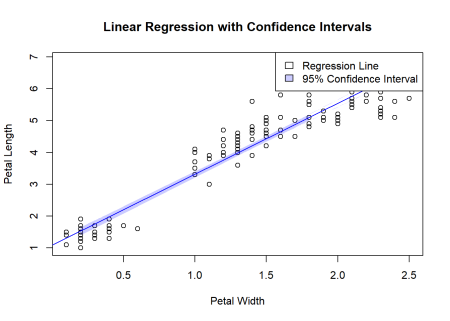
A regression line with a surrounding confidence band illustrates how uncertainty in the slope estimate produces a range of plausible lines. The band widens or narrows depending on the standard error and the critical value $t^</em>$. This example uses the Iris dataset, which includes extra contextual detail not required by the syllabus.* Source.