Evaluating inference procedures for regression slopes requires judging whether the method used, its assumptions, and its conclusions genuinely address the research question with statistical integrity.

Understanding the Purpose of Evaluating Inference Procedures

Evaluating inference procedures involves determining whether a chosen method for analyzing quantitative data related to slopes appropriately reflects the structure of the data and the research goals.

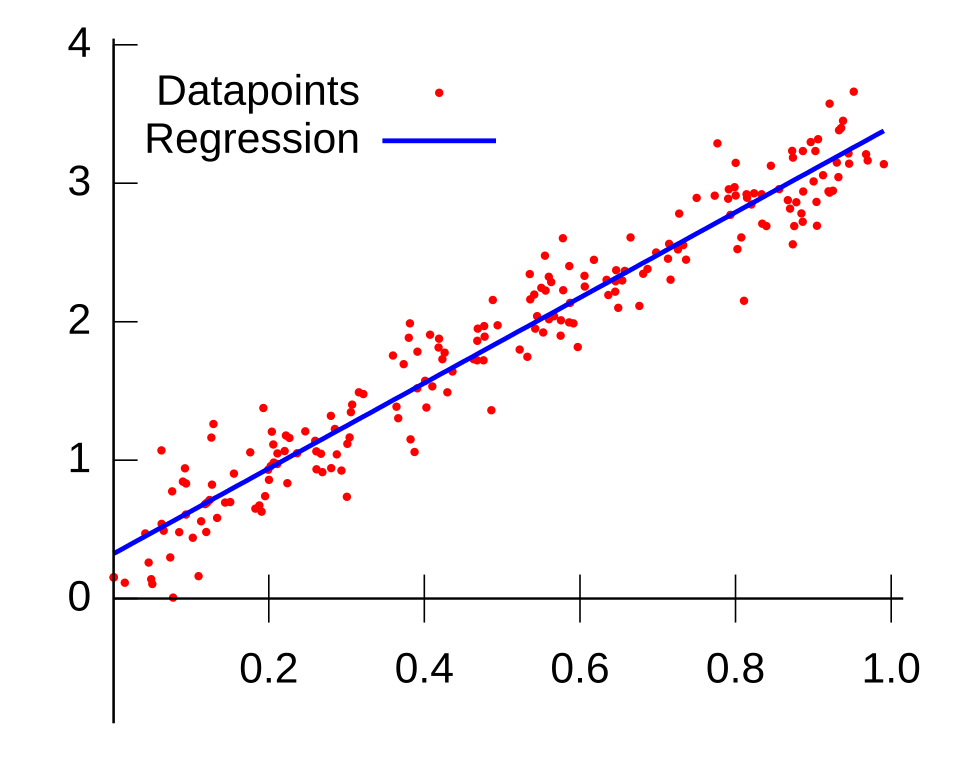
The figure displays a basic linear regression fit, illustrating how a straight-line model summarizes the trend in the data and supports evaluation of model appropriateness for slope inference. Source.

This subsubtopic emphasizes the ability to assess whether procedures such as confidence intervals for the slope, significance tests for the slope, or broader regression inference tools were correctly selected and effectively applied.

Key Considerations When Evaluating Inference Procedures

When examining the results of an inference procedure, students must judge how well the method aligns with the research objective and whether conclusions about the population slope are justified. This evaluation involves checking that:

• The procedure chosen directly answers the stated research question.

• All necessary statistical conditions were met before performing the procedure.

• The results are interpreted within the context of the sample and the population it represents.

Assessing the Effectiveness of an Inference Procedure

The effectiveness of an inference procedure depends on how well it supports the intended claim about the relationship between variables. Effective procedures provide interpretable, statistically valid statements about the slope or associated uncertainty.

Evaluating Method Selection

A central task is determining whether the correct inference procedure was chosen. For slope-related questions, this usually involves either a confidence interval (for estimation) or a significance test (for hypothesis testing). Students should assess whether the chosen method fits the research aim, such as estimating the true slope or evaluating whether evidence suggests a nonzero slope.

Conditions and Their Role in Evaluation

Evaluating an inference procedure always requires inspecting whether essential conditions were satisfied.

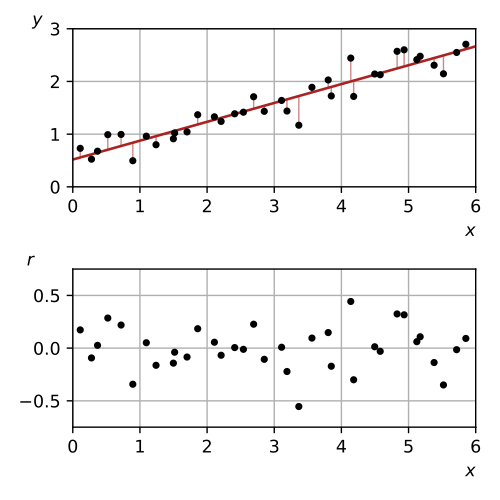
The panels illustrate both the fitted regression model and its residuals, demonstrating how linearity and constant variability conditions can be evaluated when assessing the suitability of inference procedures. Source.

These include:

• Linearity between the explanatory and response variables, verified by examining residual patterns.

• Constant variability of residuals across values of the explanatory variable.

• Independence of observations, supported by random sampling or experimental design.

• Normality of the conditional distribution of the response variable, relevant when sample sizes are moderate or small.

If these conditions were not checked or were violated, students must recognize that conclusions may lack reliability.

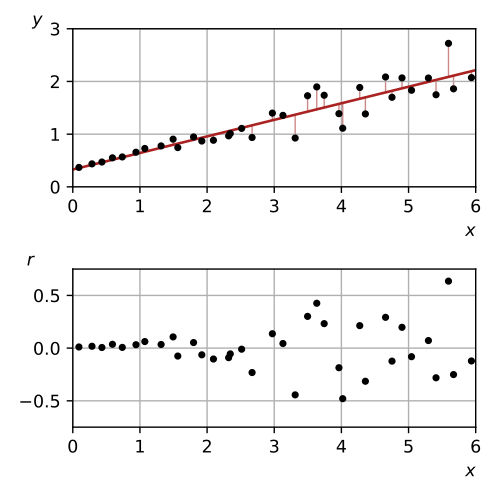
The graphic highlights increasing residual spread, indicating a violation of the constant-variability assumption. Such patterns help students evaluate the reliability of inference procedures for the slope. Source.

Aligning Data Characteristics With the Research Objective

Assessment requires confirming alignment among the data structure, the research question, and the inference method. A procedure is appropriate only when it meaningfully addresses the claim being made and respects the limitations of the dataset.

Components of Alignment

Students should reflect on several layers of alignment:

• Whether the sample represents the population of interest.

• Whether the form of the data supports linear modeling.

• Whether the chosen inference method captures the type of uncertainty relevant to the research objective.

Critical Analysis of Results From Inference Procedures

Critical analysis involves examining how well the reported results answer the research question, considering both statistical reasoning and contextual interpretation.

Evaluating Confidence Interval Results

A confidence interval gives a range of plausible values for the population slope. Students should evaluate whether:

• The interval meaningfully informs the research question.

• The width of the interval reflects reasonable precision given the sample size.

• The interpretation references the population and acknowledges the probabilistic nature of interval estimation.

Evaluating Significance Test Results

For a significance test, evaluation focuses on whether the test statistic, p-value, and conclusions logically support or fail to support the claim about the slope. Students should also consider whether the significance level used is appropriate and clearly stated.

Criteria for Determining the Appropriateness of an Inference Procedure

Using structured criteria helps ensure a robust evaluation. Students should examine the following:

• Whether the research question pertains to estimation or hypothesis testing.

• Whether the statistical method directly produces the type of information needed.

• Whether assumptions were verified and justified.

• Whether the conclusions stay within the limits of the data and analytical method.

List of Evaluation Steps

Students can apply the following steps when evaluating any inference procedure involving slopes:

• Identify the research objective and determine whether it aligns with the chosen inference method.

• Check whether all required conditions were assessed and met.

• Determine whether the interpretation of results correctly references the slope in context.

• Evaluate whether the selected method and conclusions appropriately reflect data limitations.