OCR Specification focus:
‘Choose appropriate SI and derived units for all measurements, ensuring unit consistency and correct use of prefixes where relevant.’
Understanding and applying correct scientific units ensures precision, clarity, and comparability in all experimental data. Consistent use of SI units allows reliable communication and interpretation of physical quantities.
The Role of Units in Physics
Units form the foundation of measurement in physics, providing meaning to numerical values. A numerical result without a unit is meaningless because it lacks a defined scale. The International System of Units (SI) provides a universal framework to maintain consistency across all measurements, experiments, and analyses.
Importance of Using Standard Units
Ensures comparability of results across different laboratories and studies.
Reduces confusion caused by multiple measurement systems.
Supports accuracy and reliability when applying mathematical relationships and equations.
Maintains clarity when reporting data in tables, graphs, and written reports.
The SI System
The SI system (Système International d’Unités) defines base units, from which all other physical quantities can be derived. Each base unit represents a fundamental physical dimension.
SI Base Units
Length (metre, m)
Mass (kilogram, kg)
Time (second, s)
Electric current (ampere, A)
Temperature (kelvin, K)
Amount of substance (mole, mol)
Luminous intensity (candela, cd)
These seven quantities form the building blocks for all derived quantities used in physics.
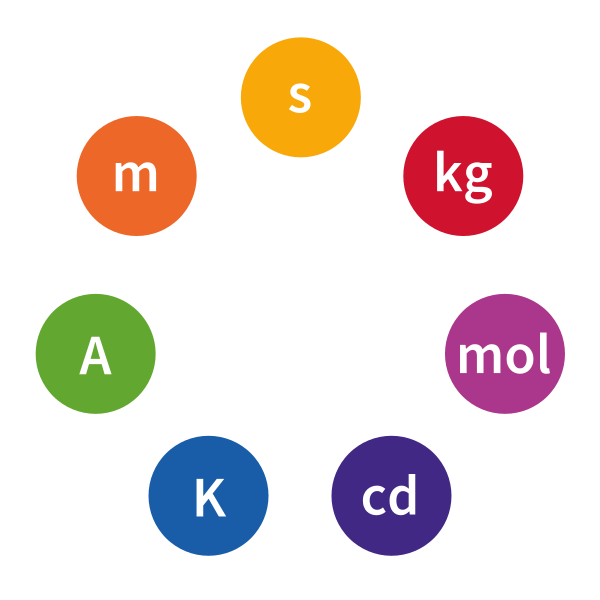
Seven SI base units—metre (m), kilogram (kg), second (s), ampere (A), kelvin (K), mole (mol), and candela (cd)—with standard symbols. The diagram highlights their status as the foundations from which derived units are formed. This visual contains only required syllabus detail and avoids extra definitions. Source
Derived Units
Derived units are combinations of base units used to describe physical quantities that are defined through relationships between the base quantities.
Derived Unit: A unit obtained by combining base units according to the algebraic relationship defining the physical quantity.
Examples of common derived units include:
Newton (N) for force: derived as kg·m·s⁻².
Joule (J) for energy: derived as kg·m²·s⁻².
Pascal (Pa) for pressure: derived as N·m⁻² or kg·m⁻¹·s⁻².
Coulomb (C) for charge: derived as A·s.
Volt (V) for potential difference: derived as J·C⁻¹ or kg·m²·s⁻³·A⁻¹.
Correct application of derived units allows equations and results to remain dimensionally consistent.
Dimensional Consistency and Unit Checking
Dimensional analysis ensures that both sides of an equation have the same combination of units. This process acts as a powerful check on the correctness of physical equations and data.
Dimensional Analysis: The method of verifying physical relationships by comparing the dimensions of the quantities involved.
To check dimensional consistency:
Express all quantities in base units.
Simplify both sides of the equation.
Ensure both sides have identical dimensional form.
If dimensions do not match, an error exists in the mathematical or conceptual reasoning of the formula.
Using SI Prefixes
Physical quantities can vary widely in magnitude, so SI prefixes simplify the expression of very large or very small numbers. Prefixes denote multiples or submultiples of base units by powers of ten.
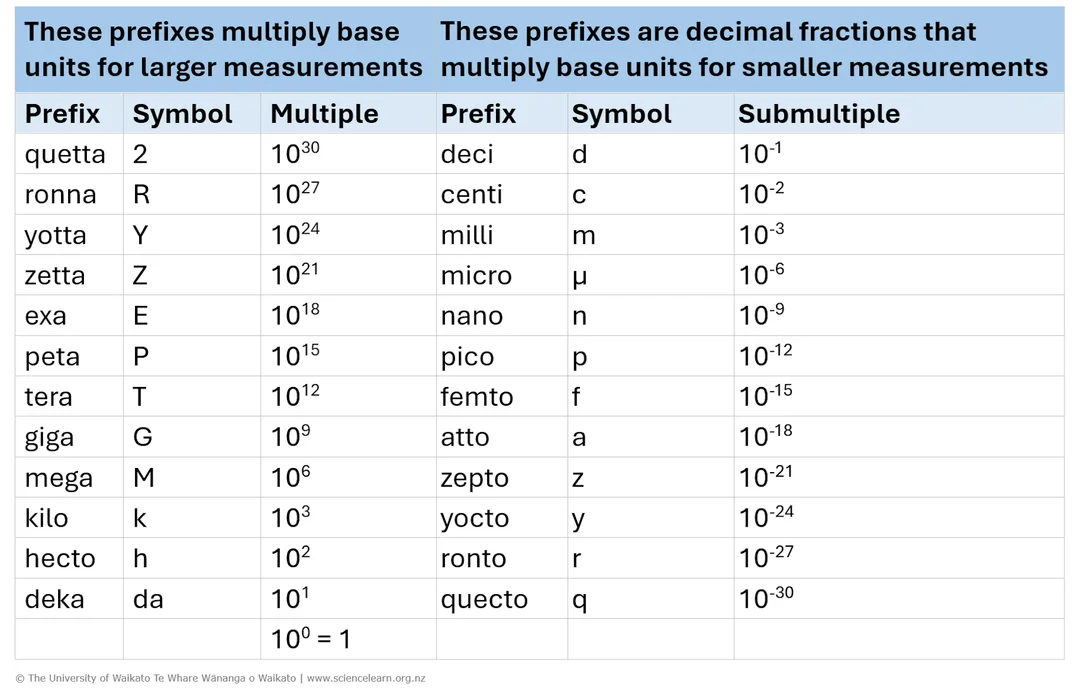
A concise SI prefixes table from quetta (Q, 10³⁰) down to quecto (q, 10⁻³⁰) with names and symbols. This supports correct prefix selection and unit consistency in data recording. The chart includes the full set of 24 prefixes, which goes beyond the most common school usage; this extra detail is acceptable but not strictly required by the syllabus. Source
Common SI Prefixes
Giga (G) – 10⁹
Mega (M) – 10⁶
Kilo (k) – 10³
Milli (m) – 10⁻³
Micro (μ) – 10⁻⁶
Nano (n) – 10⁻⁹
Correct use of prefixes improves readability and accuracy when recording or analysing data. For example, expressing 0.000001 s as 1 μs provides clarity and reduces transcription errors.
Unit Conversion
In experimental work, measurements are often taken using different scales or instruments. Therefore, the ability to convert between units accurately is essential.
To convert:
Identify the relationship between the given unit and the desired SI unit.
Multiply or divide by the appropriate conversion factor.
Maintain significant figures consistent with measurement precision.
EQUATION
—-----------------------------------------------------------------
Conversion Relationship:
Quantity (in desired unit) = Quantity (in original unit) × Conversion factor
Conversion factor = Ratio between equivalent magnitudes in two units
—-----------------------------------------------------------------
After conversion, units must still align dimensionally with the quantity being measured. Failure to convert consistently leads to major calculation errors and incorrect conclusions.
Applying Units in Data Presentation
When recording or presenting data:
Always include units in column headings of tables (e.g. “Length / m”).
Do not repeat units within each entry—apply them in headings only.
Maintain unit consistency across all columns, graphs, and calculations.
If a non-SI unit is used by necessity (e.g. minutes, °C), always convert to SI units during analysis to maintain standardisation.
Compound and Complex Units
Many practical quantities involve multiple units combined through division or multiplication. These are known as compound units.
For example:
Speed: metres per second (m·s⁻¹)
Density: kilograms per cubic metre (kg·m⁻³)
Power: joules per second (J·s⁻¹), equivalent to watts (W)
When handling compound units:
Keep the numerator and denominator clear.
Use negative indices (e.g. s⁻¹ instead of /s) for simplicity and to facilitate algebraic manipulation.
Check that the final expression maintains dimensional coherence with the underlying physical relationship.
Significance of Unit Consistency
Consistent use of correct units ensures:
Accuracy in mathematical calculations.
Validity of derived physical relationships.
Ease of error checking through dimensional analysis.
Credibility and transparency in scientific reporting.
In OCR A-Level Physics, accurate application of SI and derived units is assessed throughout both written and practical components. Every experimental design, data presentation, and calculation must reflect an understanding of unit consistency, dimensional integrity, and appropriate prefix use.
FAQ
SI base units define how physical quantities are measured, such as the metre or the second. Fundamental constants, like the speed of light (c) or Planck’s constant (h), are fixed physical quantities used to define some of these base units.
For example:
The metre is defined using the speed of light in vacuum.
The second is defined by the frequency of radiation from a specific transition in caesium-133 atoms.
Constants are not units themselves but provide the universal standards that underpin unit definitions.
Non-SI units are occasionally used for practicality, familiarity, or convenience within specific contexts. For example, astronomers may use light-years, and engineers often use bar or electronvolts.
However, these are usually converted to SI units for calculation and comparison. OCR exam questions may include non-SI quantities, but marks depend on demonstrating understanding by converting correctly to SI units before analysis.
Dimensional analysis checks whether an equation is physically valid by ensuring both sides have the same dimensional structure.
If the dimensions differ, the equation cannot represent a real physical relationship.
To use dimensional analysis:
Express each variable in its base units.
Simplify each side separately.
Compare both sides — they must match.
This method cannot confirm a numerical constant but ensures consistency and correctness of relationships.
Prefixes should be avoided when they make values unclear or inconsistent with related quantities. For example, mixing millimetres and metres in the same table can cause confusion and lead to calculation errors.
In professional reporting:
Use prefixes only when they simplify reading (e.g. μm for wavelengths).
Avoid applying multiple prefixes to related quantities within the same data set.
Consistency across all data is more important than brevity.
The hertz is defined as one cycle per second, so its base unit is s⁻¹. It derives from the SI base unit for time, the second.
Although used frequently, it depends on another base unit rather than being fundamental itself. This is the case for many familiar quantities — for example, newtons (kg·m·s⁻²) and joules (kg·m²·s⁻²) are also derived from combinations of base units.
Practice Questions
Question 1 (2 marks)
State two advantages of using SI units when reporting measurements in physics experiments.
Mark scheme:
1 mark for stating that SI units ensure consistency and allow results to be compared internationally.
1 mark for explaining that they avoid confusion caused by using multiple or non-standard measurement systems.
Question 2 (5 marks)
A student measures the period of a pendulum and records it as 0.85 minutes. They calculate the frequency using the equation:
frequency = 1 / period
(a) Convert the period into SI units. (2 marks)
(b) Calculate the frequency in hertz (Hz). (1 mark)
(c) Explain why expressing the result in hertz is more appropriate than using cycles per minute. (2 marks)
Mark scheme:
(a)
1 mark for converting minutes to seconds: 0.85 min × 60 = 51 s.
1 mark for correctly stating that the SI unit of time is the second (s).
(b)
1 mark for correct frequency calculation: 1 / 51 = 0.0196 Hz (accept 0.02 Hz with appropriate rounding).
(c)
1 mark for stating that hertz is the SI derived unit for frequency (equivalent to s⁻¹).
1 mark for explaining that using hertz maintains unit consistency with other physical quantities and allows straightforward comparison and use in equations.

