Capacitor energy equations provide a quantitative way to determine how much energy an isolated or circuit-connected capacitor can store when charged. These relationships arise from fundamental definitions of charge, potential difference, and capacitance, and allow prediction of how physical changes in a capacitor influence its stored electrical energy.

The Energy Stored in an Electric Field

The key idea underpinning capacitor energy storage is that separating charge across two plates creates an electric field. Work must be done to move charge onto the plates, and this work becomes stored energy. As more charge accumulates, the potential difference increases proportionally, so the work done is not constant per unit charge. Instead, it forms a rising relationship that leads to the three interchangeable energy equations used in A-Level Physics.

Before using these equations, it is important to understand the underlying quantities, particularly charge, potential difference, and capacitance, because their definitions determine how the equations relate to one another.

The concept of charge accumulation allows us to relate the plate separation, electric field strength, and potential difference across a capacitor.

A capacitor’s ability to store charge at a given potential difference is expressed through its capacitance.

This means a capacitor with a higher capacitance can store more charge for the same potential difference. As charging continues, increasing energy is needed to move additional charge against the higher p.d., which leads to the characteristic energy expressions.

Deriving the Capacitor Energy Equations

The three OCR-required equations describe the same physical energy using different variables. They originate from the p.d.–charge relationship and represent the area under a graph of V against Q. Because this graph is a straight line through the origin, the area—and thus the energy stored—is a triangle.

Graphically, the energy stored by a capacitor is equal to the area under a graph of potential difference V against charge Q.

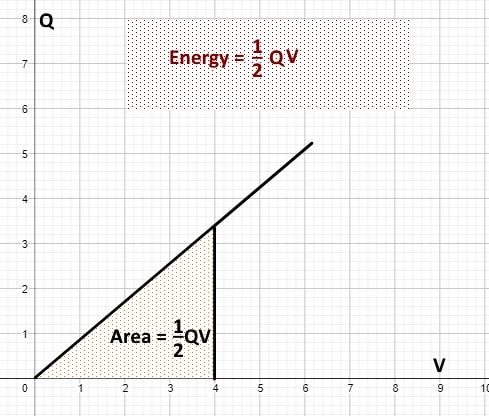
A Q–V graph showing the triangular region representing the work done to charge a capacitor. The shaded area corresponds to the energy stored, leading directly to the equation W = ½QV. This illustrates how the geometric area under the graph defines the capacitor’s stored energy. Source.

The first equation encountered by most students focuses directly on the charge and final potential difference of the capacitor.

EQUATION
—-----------------------------------------------------------------
Energy Stored in a Capacitor (W) = ½ Q V
W = Energy stored (joules, J)
Q = Charge stored (coulombs, C)
V = Potential difference across capacitor (volts, V)
—-----------------------------------------------------------------

This relationship demonstrates that energy storage depends jointly on how much charge a capacitor holds and the potential difference it has reached. Since both Q and V rise during charging, the factor of ½ reflects the increasing work required as the plates approach their final separation of charge.

Although W = ½QV is the most intuitive graph-based form, many practical situations require equations expressed in terms of capacitance and either charge alone or voltage alone. These rearrangements come from substituting Q = CV into the above equation.

After examining the version using Q and V, it is helpful to express energy purely in terms of charge when potential difference is less convenient to measure.

EQUATION
—-----------------------------------------------------------------
Energy Stored Using Charge Only (W) = Q² / (2C)
W = Energy stored (J)
Q = Charge stored (C)
C = Capacitance (F)
—-----------------------------------------------------------------

This equation highlights that a capacitor with larger capacitance stores less energy for a given charge, because a larger capacitor requires less work to hold that charge at a lower potential difference.

A single sentence must separate this from the next equation block to meet the formatting requirement, so note that the final standard form places emphasis instead on the potential difference across the capacitor plates.

EQUATION
—-----------------------------------------------------------------
Energy Stored Using Voltage Only (W) = ½ C V²
W = Energy stored (J)
C = Capacitance (F)
V = Potential difference (V)
—-----------------------------------------------------------------

This form is extremely useful when analysing circuits where the supply voltage is known but the charge is not directly measurable. It immediately shows that stored energy increases with the square of the voltage, illustrating how a modest rise in potential difference can significantly increase stored energy.

Choosing the Most Useful Equation

Because all three expressions describe the same physical quantity, the most appropriate equation depends on what information is available. Students should consider the following:

When Q and V are both known

Use W = ½QV, as this relates most clearly to the work done in establishing the electric field.

When Q is known but V is not

Use W = Q²/(2C), which eliminates the need to calculate potential difference.

When V is known but Q is not

Use W = ½CV², especially useful in circuit design or when working with known supply voltages.

Key Points for Examination

• The energy stored is the work done to transfer charge to the capacitor plates.

• The factor ½ appears because charge and potential difference increase proportionally during charging.

• All three equations must be memorised and recognised as equivalent.

• Understanding variable relationships allows prediction of how changes in capacitance, charge, or voltage affect stored energy.

In all three forms of the energy equation, the same quantity is being described: electrostatic potential energy stored in the electric field between the capacitor plates.

Diagram of a parallel-plate capacitor showing the plates, separation, and dielectric region. The energy given by the three equations is stored in the electric field between these plates. Labels such as A and d add structure detail beyond the syllabus but help link the equations to the physical capacitor. Source.