A uniformly charged sphere behaves externally like a single concentrated charge at its centre, allowing simplified electric-field modelling that is foundational for Coulomb-law and field-strength applications.

Spherical Charge as a Point Model

A uniformly charged sphere is a common physical and theoretical model used in electrostatics. When a sphere carries charge that is evenly distributed across its surface or throughout its volume, the electric field it produces outside the sphere behaves in a very specific and extremely useful way. For points outside the sphere, the distribution of charge can be treated as if all the charge were concentrated at a single point at the sphere’s centre.

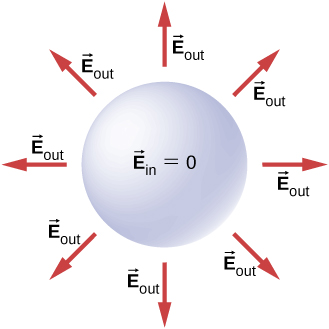
Electric field of a positively charged conducting sphere. The radial field lines show that, outside the sphere, the field is identical to that of a single point charge at the centre. The diagram also notes that the field inside the conductor is zero, which is extra detail beyond this specific OCR subsubtopic but consistent with the same spherical symmetry argument. Source.

This model arises from symmetry considerations: because charge is distributed identically in all directions, the resulting field must also be radially symmetric, pointing directly away from or towards the centre depending on the sign of the charge.

Why the Model Works

The model is based on the principle that spherical symmetry forces electric field contributions from different parts of the sphere to combine in such a way that the external field is indistinguishable from that of a single central charge. This is only valid when no part of the observation point lies inside the charged material. The simplicity of this model is essential for reducing complex distributions to manageable forms.

Key Features of the Model

• Applies only to points outside the sphere
  The field inside a sphere behaves differently and cannot be treated using the point-charge approximation (though this belongs to other subsubtopics).

• Requires uniform charge distribution
  Non-uniform distributions break the symmetry and invalidate the model.

• Allows use of point-charge equations
  Any formula normally used for a point charge may be applied to a uniformly charged sphere when considering its external field.

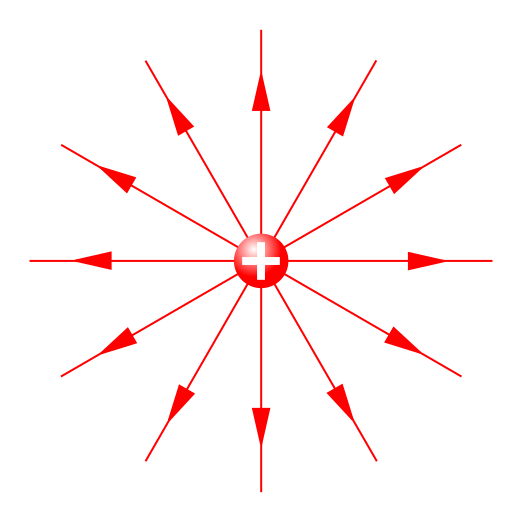
Radial electric field lines around a single positive point charge. The equal angular spacing of the arrows shows that the field has the same magnitude at a given distance in every direction, matching the symmetry of a uniformly charged sphere. This diagram does not explicitly show a sphere, but it represents the field pattern that a uniformly charged spherical conductor produces outside its surface when modelled as a point charge at the centre. Source.

• Supports both positive and negative charge systems
  Only direction changes; the magnitude behaviour remains identical.

Because OCR requires students to model a uniformly charged sphere as a point charge at its centre for field calculations, this understanding should be applied whenever calculating field strength, electric force, or potential around spherical charged bodies.

Mathematical Implications

When the model applies, one may use the standard point-charge expressions for field strength. In practice, this means the electric field of a uniformly charged sphere of total charge Q at a distance r from its centre (where r is greater than the sphere’s radius) is given by the familiar inverse-square behaviour.

EQUATION
—-----------------------------------------------------------------
Electric Field of a Spherical Charge (E) = (1 / (4πɛ₀)) · (Q / r²)
E = Electric field strength in newtons per coulomb (N C⁻¹)
Q = Total charge on the sphere in coulombs (C)
r = Distance from the centre of the sphere in metres (m)
ɛ₀ = Permittivity of free space in farads per metre (F m⁻¹)
—-----------------------------------------------------------------

This equation reflects the fact that only the total charge matters, not how that charge is spread across the sphere, so long as it remains uniform and spherical.

The ability to simplify a real three-dimensional distribution to a single-point source is powerful. It is used extensively in modelling planets, charged droplets, metallic spheres, and subatomic systems that approximate spherical symmetry.

Physical Interpretation

Thinking physically about why the model works deepens understanding. Each small portion of the sphere contributes a component of electric field at the observation point. For every piece of charge creating a field with a slight angle above the radial line, there is a corresponding element whose field lies symmetrically below it. The sideways components cancel due to symmetry, leaving only radial components. The result is a perfectly radial electric field that matches the shape and behaviour of that from a point charge.

Important Consequences

• Radial direction of field lines
  Outside the sphere, electric field lines extend straight outward or inward, exactly as they would for a point charge.

• Field magnitude decreases with r²
  Because the field is radial and symmetric, its magnitude obeys the inverse-square law.

• Field mapping matches that of a point charge
  When drawing or interpreting field patterns, the sphere can be visualised simply as a point from which lines emanate or converge.

This equivalence makes field-mapping experiments and theoretical diagrams significantly simpler for students and physicists alike.

Practical Use in A-Level Problems

In OCR A-Level Physics, the point-model assumption is invoked whenever the problem states or implies:

• the object is a sphere,

• the charge is uniform,

• and calculations involve points outside the sphere.

Under these conditions, students should:

• Replace the sphere with a point charge of value Q at its centre.

• Use point-charge equations for electric field, force, or potential.

• Interpret direction and field patterns using radial symmetry.

This approach enables efficient problem-solving and aligns directly with the specification’s requirement to model a uniformly charged sphere as a point charge at its centre for field calculations.