OCR Specification focus:
‘Use the principle of moments: for equilibrium, sum of clockwise moments equals sum of anticlockwise moments.’
The principle of moments is a fundamental concept in mechanics that explains how turning effects balance in static equilibrium, forming the foundation for analysing rotational forces.
Understanding Moments
The Concept of a Moment
A moment is the turning effect of a force about a pivot or axis. It measures how effectively a force causes rotation.
Moment of a Force: The product of the force and the perpendicular distance from the line of action of the force to the pivot point.
EQUATION
—-----------------------------------------------------------------
Moment (M) = Force (F) × Perpendicular distance from pivot (d)
M = measured in newton metres (N m)
F = force in newtons (N)
d = perpendicular distance in metres (m)
—-----------------------------------------------------------------
Moments act in two possible rotational directions — clockwise or anticlockwise — depending on which side of the pivot the force is applied. The direction is determined by the force’s tendency to rotate the object.
Clockwise and Anticlockwise Moments
Clockwise moments act in the direction of a clock’s hands.
Anticlockwise moments act in the opposite direction.
In equilibrium situations, these opposing moments balance perfectly, ensuring that there is no net rotation about the pivot.
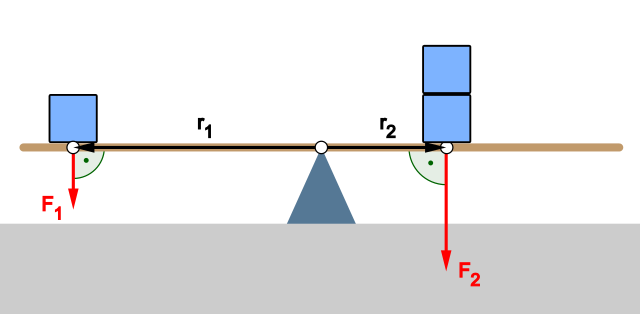
Principle of moments on a seesaw. Equal and opposite moments about the pivot balance, giving zero resultant moment and no angular acceleration. The figure visualises clockwise versus anticlockwise turning effects at equilibrium. Source
The Principle of Moments
Statement of the Principle
The principle of moments states that for a system in rotational equilibrium:
The sum of the clockwise moments about a point equals the sum of the anticlockwise moments about that same point.
This principle applies to any object that is stationary and not rotating. It forms a critical condition for rotational equilibrium, which complements the condition for translational equilibrium (when the resultant force on an object is zero).
EQUATION
—-----------------------------------------------------------------
∑ Clockwise Moments = ∑ Anticlockwise Moments
—-----------------------------------------------------------------
This relationship ensures that there is no net torque, meaning the object remains stable and does not begin to turn.
Physical Meaning
If the sum of moments in one direction exceeds the other, the object will rotate until the torques balance again. The principle therefore enables the prediction of how and where forces must act to maintain stability.
Relationship to Force Equilibrium
For complete equilibrium, both the translational and rotational conditions must be satisfied:
Resultant force = 0 → No linear acceleration.
Resultant moment = 0 → No angular acceleration.
An object can meet the first condition but still rotate if its moments are unbalanced. Therefore, applying the principle of moments is essential for determining static balance.
Applying the Principle of Moments
Step-by-Step Method
To apply the principle of moments in a problem:
Identify the pivot point — choose any convenient location about which to calculate moments.
Determine all acting forces — include weights, tensions, reactions, or applied forces.
Calculate perpendicular distances — measure each force’s perpendicular distance from the pivot.
Assign directions — label each moment as clockwise or anticlockwise.
Apply the principle of moments — equate total clockwise and anticlockwise moments.
Solve for the unknown quantity — typically a force, distance, or reaction.
Each step reinforces the conceptual understanding that balance in rotation depends on the interplay between magnitude of force and distance from the pivot.
Importance of Perpendicular Distance
The perpendicular distance is crucial: only the component of the force acting at right angles to the lever arm contributes to the moment. Any component parallel to the arm does not create rotation.
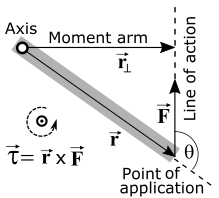
Lever arm and line of action. The diagram shows the force F, the pivot/axis, the line of action, and the perpendicular lever arm used to compute the moment. It illustrates why only the perpendicular component of F creates a turning effect. Source
Common Situations in Physics
The principle of moments is central to understanding the operation of:
Levers — such as seesaws, crowbars, and spanners.
Beams and bridges — where the distribution of weight must maintain equilibrium.
Balances and scales — where moments determine the equality of weights.
Doors and gates — where the handle position maximises moment arm length for ease of use.
In all these cases, the moment is adjusted either by changing the force applied or the distance from the pivot to maintain balance.
Real-World and Engineering Applications
Structural Design
In engineering, the principle of moments ensures stability in structures such as cranes, bridges, and buildings. Engineers must verify that:
All support reactions create counterbalancing moments to resist tipping.
Loads are distributed symmetrically, preventing unwanted rotation.
By calculating moments about strategic points, designers can predict how loads transfer through beams and supports.
Safety and Efficiency
The concept also underpins the design of tools and machinery to maximise mechanical advantage. For instance:
Increasing the handle length of a spanner doubles the moment for the same applied force.
In wheelbarrows, the pivot and load positions are optimised so a smaller effort balances a larger weight.
These designs apply the principle of moments to reduce human effort while maintaining equilibrium.
Moments in Biological and Environmental Contexts
Beyond engineering, the same principle governs biomechanical systems. Muscles generate forces about joints, creating moments that move limbs. The bone acts as a lever, and equilibrium between muscle force and load maintains posture or controls movement.
In natural phenomena, trees and structures resist tipping moments caused by wind forces. Their roots or foundations provide equal and opposite moments to sustain stability.
Vector Nature of Moments
Moments are vector quantities because they have both magnitude and direction (clockwise or anticlockwise). The direction can also be described using the right-hand rule — curling the fingers in the rotation direction shows the moment vector’s orientation along the thumb.
When multiple forces act at different points, their vector sum determines the net torque about the pivot. If this net torque equals zero, rotational equilibrium is maintained.
Torque and Moment Equivalence
In many contexts, the terms moment and torque are interchangeable. However, torque often refers to rotational effect about an axis in machines or engines, while moment is used more generally in static systems.
Torque: The rotational effect of a force about an axis, equal to the product of the force and the perpendicular distance from the axis of rotation.
While torque is expressed in newton metres (N m), the physical interpretation is identical to that of a moment.
Influence of Force Direction
If the force does not act perpendicularly, only its perpendicular component contributes to the effective moment. The relationship can be expressed as:
EQUATION
—-----------------------------------------------------------------
Moment = Force × Distance × sin(θ)
θ = Angle between force and lever arm (degrees or radians)
—-----------------------------------------------------------------
This relationship highlights why the greatest turning effect occurs when a force acts at right angles to the lever arm.
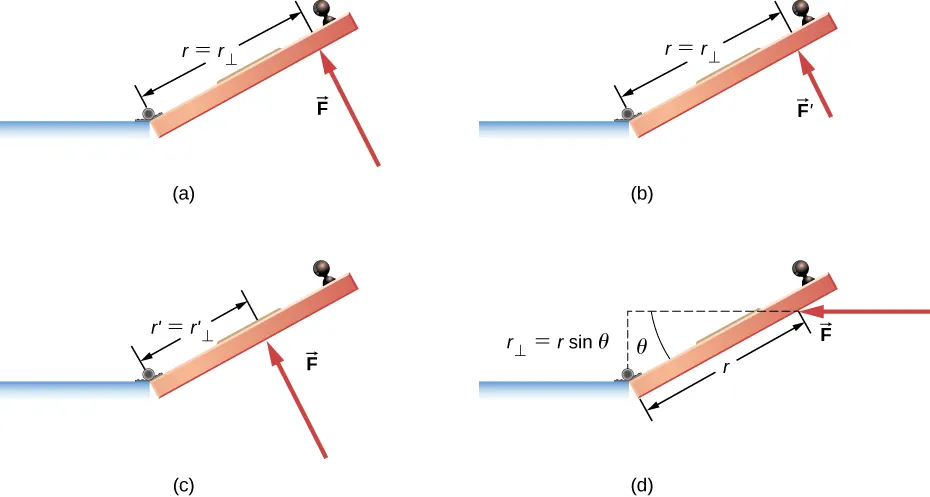
Torque on a door for different distances and angles. The panels compare how distance from the hinge and angle of application change the torque. At 90° the moment is maximal; at smaller angles the effective perpendicular component—and thus the torque—is reduced. Source
Summary of Key Concepts
A moment measures the turning effect of a force about a pivot.
The principle of moments ensures rotational equilibrium by equating clockwise and anticlockwise moments.
Real-world systems — from levers to bridges — depend on this balance for stability and efficiency.
Accurate analysis requires considering force magnitude, direction, and perpendicular distance from the pivot.
FAQ
Moment calculations are highly sensitive to distance measurements, as even small angular or linear errors can cause significant discrepancies.
Common sources of uncertainty include:
Difficulty measuring the perpendicular distance precisely.
Slight misalignment between force direction and lever arm.
Reading errors when using rulers or force meters.
To reduce uncertainty:
Use plumb lines or set squares to confirm perpendicularity.
Take repeated readings and calculate the mean.
Keep lever arms long to make distance errors less proportionally significant.
Moving the pivot changes the perpendicular distances of all forces, altering their moments. If the pivot shifts closer to a force, that force’s moment decreases because the moment arm (distance) becomes smaller.
To maintain equilibrium, another force must produce a larger opposing moment, either by increasing its force or acting at a greater distance. This concept is crucial in systems like balances and cranes, where pivot placement controls mechanical advantage.
An irregular object has a centre of mass that may not lie at its geometric centre. The distribution of weight determines where this point lies, and thus how the object balances.
When supported directly beneath its centre of mass, the sum of moments about that point is zero, and the object remains level. If displaced, the unequal moments cause rotation until equilibrium is re-established or the object tips over.
The moment depends on both the force and its distance from the pivot. A mass placed very close to the pivot exerts a small moment because its lever arm is short.
Therefore, even a relatively large weight near the pivot contributes minimally to rotation. This is why fulcrums or supports are often placed near heavy components in machinery — to reduce their turning effect and maintain balance.
Yes, but only if the object is in rotational equilibrium — that is, there is no angular acceleration. If the sum of moments is not zero, the object will start rotating or change its rotational speed.
In dynamic cases, Newton’s second law for rotation applies: the net moment equals the rate of change of angular momentum. The principle of moments is therefore a special case of this, used when net torque equals zero.
Practice Questions
Question 1 (2 marks)
A uniform beam is balanced horizontally on a pivot placed 0.8 m from one end. A weight of 40 N hangs from the shorter end, and the beam remains in equilibrium.
State the principle of moments and write the equation that must be satisfied for the beam to remain in equilibrium.
Mark Scheme (2 marks)
(1 mark) Correct statement of the principle of moments: For an object in equilibrium, the sum of the clockwise moments about a point equals the sum of the anticlockwise moments about that same point.
(1 mark) Correct equilibrium condition written as an equation: Σ clockwise moments = Σ anticlockwise moments (or equivalent algebraic form such as W1 × d1 = W2 × d2).
Question 2 (5 marks)
A uniform metre rule of weight 2.0 N is supported horizontally by a pivot placed at the 30 cm mark. A 4.0 N weight is hung from the 0 cm end of the rule.
(a) State the condition required for the rule to be in rotational equilibrium. (1 mark)
(b) Calculate the weight that must be hung from the 90 cm mark to keep the rule in equilibrium. (4 marks)
Mark Scheme (5 marks)
(a) (1 mark)
The sum of the clockwise moments about the pivot equals the sum of the anticlockwise moments.
(b) (4 marks)
(1 mark) Correct identification of forces and distances:
4.0 N weight acts 0.30 m from the pivot (anticlockwise).
Weight of the rule (2.0 N) acts at its centre of gravity (50 cm mark), i.e. 0.20 m from the pivot (clockwise).
Unknown weight W acts 0.60 m from the pivot (clockwise).
(1 mark) Setting up the moment balance equation: 4.0 × 0.30 = (2.0 × 0.20) + (W × 0.60)
(1 mark) Substitution and correct rearrangement: 1.20 = 0.40 + 0.60W
(1 mark) Correct final answer with unit: W = 1.33 N (accept answers between 1.3 and 1.4 N).

