In physics, equilibrium describes a state where all forces and torques acting on a body balance perfectly, ensuring no change in motion or rotation. Understanding equilibrium enables accurate analysis of structures, mechanisms, and natural systems.

The Nature of Equilibrium

A body is in equilibrium when both its translational and rotational motions remain constant — meaning there is no acceleration and no angular acceleration. This occurs when all external forces and torques are balanced. For equilibrium analysis, two essential conditions must always be met: one concerning forces, and the other concerning torques.

Translational Equilibrium

Translational equilibrium refers to the situation where the net (resultant) force on a body is zero. This ensures that the body does not accelerate linearly and either remains at rest or continues moving at a constant velocity.

EQUATION
—-----------------------------------------------------------------
Condition for Translational Equilibrium: ΣF = 0
ΣF = Vector sum of all forces acting on the body (N)
—-----------------------------------------------------------------

This equilibrium condition applies separately in both horizontal and vertical directions, which is particularly useful for resolving forces acting at angles or on inclined surfaces.

Rotational Equilibrium

Rotational equilibrium is achieved when the sum of all moments (torques) about any point is zero. This ensures that the body does not rotate or, if already rotating, continues at a constant angular velocity.

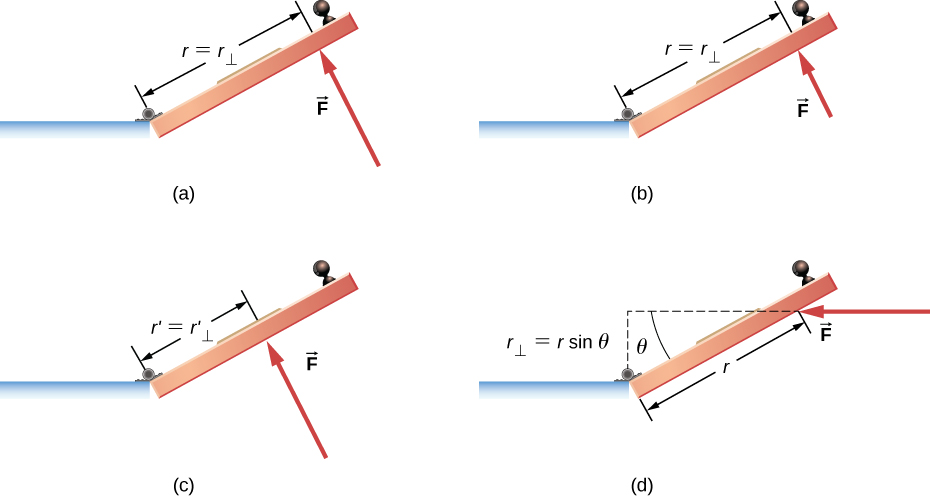
Torque is the rotational effectiveness of a force about a pivot. The figure shows how the same force produces different torques depending on perpendicular distance and angle, distinguishing clockwise and counterclockwise rotation. This supports the condition Στ = 0. Source.

EQUATION
—-----------------------------------------------------------------
Condition for Rotational Equilibrium: Στ = 0
τ = Torque or moment of a force (N m)
—-----------------------------------------------------------------

For a rigid body to be in complete equilibrium, both translational and rotational equilibrium must be satisfied simultaneously.

Forces in Equilibrium

When multiple forces act on a body, equilibrium requires that their vector sum equals zero. In diagrams, this can be visualised as the forces forming a closed polygon, typically a triangle for three coplanar forces.

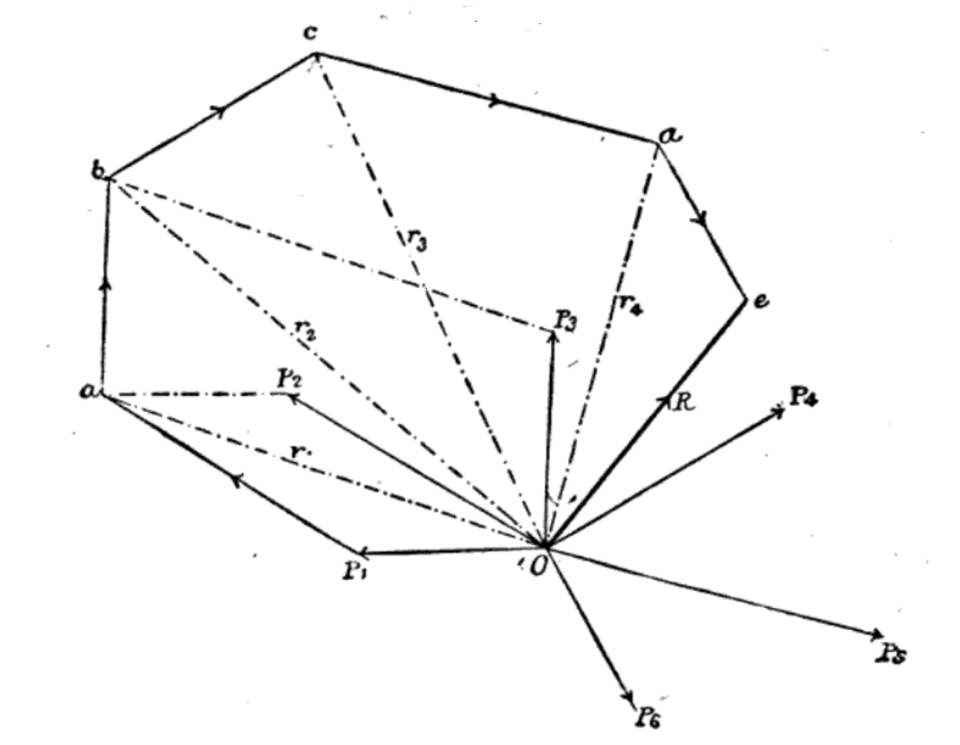
A polygon of forces represents forces tip-to-tail; closure of the polygon indicates zero resultant, i.e. translational equilibrium. For three forces, this becomes the triangle of forces used at A-Level. The historical figure shows a general polygon, but the principle is identical. Source.

Triangle of Forces

The triangle of forces is a graphical method for representing equilibrium involving three coplanar forces acting at a point.

This concept arises directly from vector addition: if three forces are in equilibrium, then F₁ + F₂ + F₃ = 0. When drawn tip-to-tail, the vectors form a closed triangle.

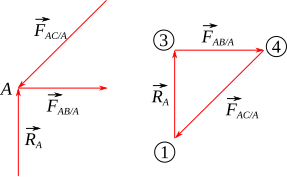
A triangle of forces diagram shows three coplanar forces in equilibrium represented by a closed triangle drawn to scale. This illustrates the OCR requirement to use the triangle of forces for three coplanar forces. Light structural node labels are present but do not affect interpretation. Source.

To apply this condition:

• Draw each force as a vector in the correct direction and magnitude.

• Connect them tip-to-tail.

• If they form a closed triangle, the body is in equilibrium.

This graphical approach simplifies analysis, particularly in static systems such as beams, supports, and suspended objects.

Coplanar Forces

Coplanar forces are forces that act within the same plane. Most equilibrium problems at A-Level assume coplanar conditions. When more than three coplanar forces act on a body, vector resolution or algebraic methods are used to confirm that the resultant force is zero.

For equilibrium under coplanar forces:

• Resolve all forces into horizontal and vertical components.

• Ensure that the sum of components in each direction is zero.

• Verify that moments about any chosen point also sum to zero.

EQUATION
—-----------------------------------------------------------------
Conditions for Coplanar Equilibrium:
ΣFₓ = 0
ΣFᵧ = 0
Στ = 0
Fₓ = Sum of horizontal components of forces (N)
Fᵧ = Sum of vertical components of forces (N)
τ = Sum of moments about a chosen point (N m)
—-----------------------------------------------------------------

These three conditions are sufficient to confirm equilibrium for planar systems.

Forces and Torques Acting Together

For equilibrium, forces and torques are interdependent. A system may have balanced forces but still rotate if torques do not balance. Conversely, balanced torques alone do not guarantee translational stability. Therefore:

• All linear forces must balance to prevent translation.

• All moments must balance to prevent rotation.

Examples include balanced beams, suspended signs, or static ladders — all depend on simultaneous fulfilment of both equilibrium conditions.

Checking Equilibrium in Practice

In practical and theoretical problems, the following structured process ensures correct analysis:

• Identify all external forces acting on the object (including weight, normal reaction, tension, and friction).

• Represent these forces with a free-body diagram.

• Resolve angled forces into perpendicular components.

• Choose a convenient pivot point for taking moments — often where unknown forces act.

• Apply equilibrium conditions systematically:

  • ΣFₓ = 0 (horizontal balance)

  • ΣFᵧ = 0 (vertical balance)

  • Στ = 0 (rotational balance)

If all conditions hold true, the object is confirmed to be in equilibrium.

Applications of the Equilibrium Conditions

The principles of equilibrium underpin many physical and engineering systems:

• Bridges and beams rely on balanced forces and torques to prevent collapse.

• Cranes and levers use moment calculations to ensure safe load limits.

• Suspended objects such as signs or lamps are designed with the triangle of forces to predict tension in cables.

• Human biomechanics applies equilibrium to analyse posture and joint forces.

These examples demonstrate how theoretical equilibrium conditions translate directly into real-world stability and design efficiency.

Key Summary of Conditions for Equilibrium

A body is in equilibrium when:

• The resultant of all forces acting on it is zero (ΣF = 0).

• The resultant of all torques about any point is zero (Στ = 0).

• For three coplanar forces, the triangle of forces can represent the equilibrium condition geometrically.

Together, these principles form the foundation for analysing both static and dynamic systems in mechanics, ensuring predictive control over motion and stability.