Newton’s second law connects force with the change in momentum of an object, providing the foundation for understanding how forces cause motion, acceleration, and interactions in physical systems.

Understanding Force and Momentum

Linear Momentum

Momentum is a fundamental quantity in mechanics that describes the motion of a body and depends on both its mass and velocity. It measures how difficult it is to stop or change an object’s motion.

Because velocity is a vector quantity, momentum is also a vector, having both magnitude and direction. The direction of momentum is always the same as that of the velocity. Objects with greater momentum require a larger force or longer time to bring to rest.

The Relationship Between Force and Momentum

Newton’s Second Law of Motion states that the net force acting on an object is equal to the rate of change of its momentum. This provides a general and powerful statement about how forces influence motion.

EQUATION
—-----------------------------------------------------------------
Newton’s Second Law (General Form): F = Δp / Δt
F = Net force acting on an object (newtons, N)
Δp = Change in momentum (kilogram metre per second, kg·m/s)
Δt = Time interval over which the change occurs (seconds, s)
—-----------------------------------------------------------------

This equation expresses that the greater the rate of change of momentum, the greater the force applied to an object. It applies to all cases, including those where the mass of an object changes (such as a rocket expelling exhaust gases).

Special Case: Constant Mass

In many typical mechanics problems, the mass of an object remains constant. In such cases, the equation for force simplifies significantly.

EQUATION
—-----------------------------------------------------------------
Special Case (Constant Mass): F = ma
F = Net force (newtons, N)
m = Mass of the object (kilograms, kg)
a = Acceleration of the object (metres per second squared, m/s²)
—-----------------------------------------------------------------

This familiar form of Newton’s Second Law links the net force directly to the acceleration of the object. It shows that for a given mass, a larger force produces a larger acceleration in the same direction as the force.

Connecting the Two Forms

When the mass is constant, the change in momentum can be written as:

Δp = mΔv

Substituting into the general form F = Δp / Δt gives:

F = m(Δv / Δt) = ma

This derivation shows that F = ma is not a separate law, but a special case of the more general F = Δp / Δt, valid only when the mass does not change. For systems like rockets, where mass changes as fuel burns, the full momentum-based form must be used.

Vector Nature of Force and Momentum

Both force and momentum are vector quantities, which means they have both magnitude and direction.

• The direction of the net force determines the direction of acceleration and the direction of the change in momentum.

• If multiple forces act on a body, the vector sum (the net force) determines the resulting motion.

• When drawing vector diagrams, the relative directions of momentum before and after an interaction help visualise the effect of forces.

Understanding this vector nature is essential for analysing situations involving motion in two dimensions, such as curved motion or collisions at angles.

Implications of Force as Rate of Change of Momentum

1. Variable Forces

In many real-world cases, the force acting on an object is not constant. For example, when a tennis ball hits a racket, the force changes over time. The momentum-based form of Newton’s second law allows us to handle such cases by considering the average force over the period of contact.

2. Time of Contact and Force Magnitude

The same change in momentum can occur through:

• A large force acting over a short time, or

• A smaller force acting over a longer time.

This relationship is crucial in applications such as car safety design, where extending the time of impact (for instance, through airbags or crumple zones) reduces the force experienced by passengers.

3. Systems with Changing Mass

For systems where mass is not constant (e.g. rockets, jet engines), the momentum formulation is essential. The thrust in a rocket arises from the rate of change of momentum of the expelled exhaust gases.

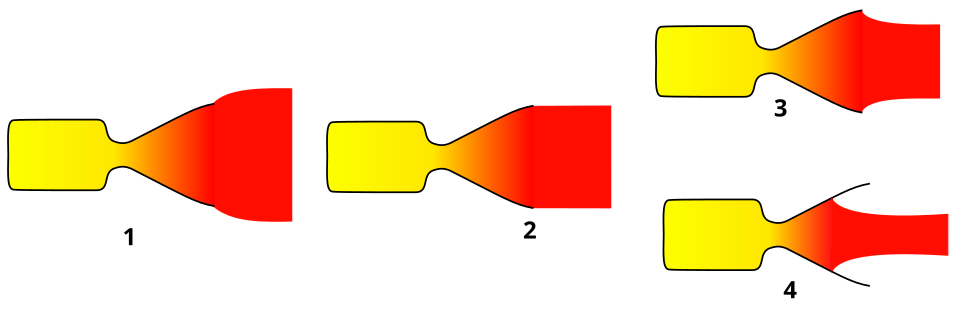
Labeled schematic of a rocket nozzle highlighting how exhaust flow expands as it leaves the chamber. It links to thrust as a momentum-change effect in a changing-mass system; the labelled expansion regimes (under/ambient/overexpanded) are informative but not required by OCR and can be skimmed. The layout is simple with minimal labels, suitable for study notes. Source

In these cases, using F = ma would be inappropriate because the system’s mass changes continuously.

Momentum Change in Multiple Directions

Since momentum is a vector, any change in its magnitude or direction implies a net force. This is important even in cases where the speed remains constant, such as uniform circular motion. Here:

• The speed of the object remains constant.

• The direction of momentum changes continuously.

• A centripetal force acts towards the centre of the circular path, continuously changing the direction of the momentum vector.

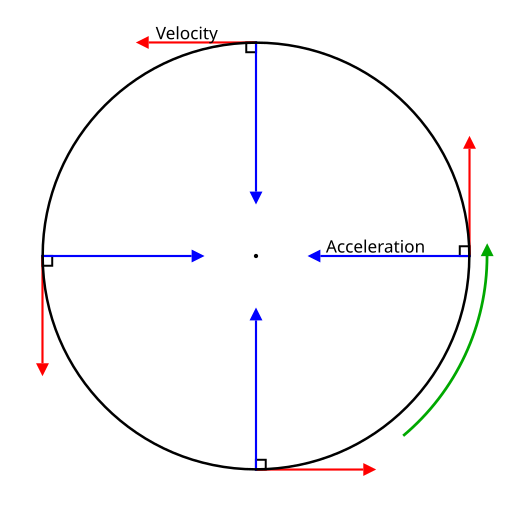
Vector diagram for uniform circular motion showing the velocity vector tangent to the path and the acceleration vector directed towards the centre. Since acceleration is towards the centre, the net force is also centripetal, changing the direction of momentum without changing its speed. Clean, uncluttered labels support vector reasoning at OCR A-Level. Source

This demonstrates that force is required to change not only the speed but also the direction of motion of an object.

Practical Contexts and Applications

Understanding force as the rate of change of momentum underpins numerous areas of physics and engineering:

• Sports physics: Analysing impacts in games such as cricket, tennis, or football, where equipment design optimises the force and contact time to control momentum transfer.

• Vehicle safety: Airbags, seatbelts, and crumple zones are designed to reduce the rate of change of momentum, thereby lowering the forces on occupants.

• Spaceflight: Rocket propulsion relies on expelling mass to generate thrust through a change in momentum of the gases.

• Industrial machinery: Machines such as presses and hammers use large momentum changes to perform work efficiently.

Each of these contexts demonstrates that understanding how forces relate to momentum allows for safer, more efficient, and more predictable designs.

Summary of Key Relationships

• Force is the rate of change of momentum: F = Δp / Δt.

• F = ma applies when mass is constant.

• Both force and momentum are vector quantities.

• Larger forces or shorter contact times produce greater momentum changes.

• The general momentum form applies universally, including systems with changing mass.