Momentum conservation is a fundamental principle of mechanics describing how the total momentum of a system remains constant when no external forces act. Understanding this allows analysis of collisions, explosions, and separations in both everyday and scientific contexts.

The Principle of Conservation of Momentum

Momentum is a quantity that expresses the motion of an object and depends on both its mass and velocity. In any closed system, where no external forces act, the total momentum before an interaction equals the total momentum after. This rule applies regardless of whether the objects involved collide or move apart.

In simple terms, momentum measures “how much motion” an object possesses and how difficult it is to stop. Since momentum is a vector, direction must always be considered — reversing direction changes the sign of momentum.

Linear Momentum and System Interactions

Momentum is described mathematically as follows:

EQUATION
—-----------------------------------------------------------------
Linear Momentum (p) = m × v
p = momentum (kg m s⁻¹)
m = mass (kg)
v = velocity (m s⁻¹)
—-----------------------------------------------------------------

For a system of interacting objects, the total momentum is the vector sum of each object’s momentum. When an event occurs, such as a collision or explosion, the sum of all individual momenta remains the same, provided the system is isolated from external forces like friction or air resistance.

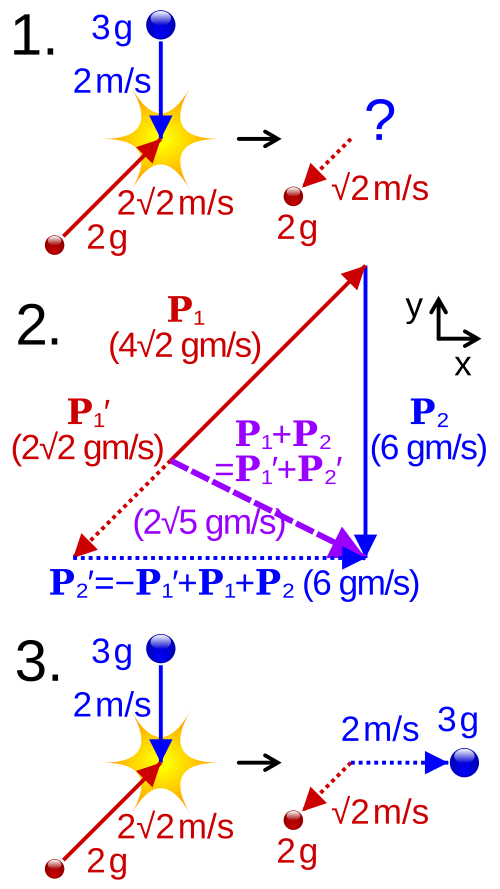
A clean head-to-tail momentum vector diagram showing before-and-after momenta for a two-object interaction. The resultant (total momentum) is unchanged, illustrating conservation in a closed system. Any specific numbers shown are illustrative and not required for the OCR specification. Source

• Closed system: No external forces act on the objects involved.

• Open system: External forces influence the motion, so total momentum may change.

• Internal forces: Forces objects exert on each other within the system; these do not affect total momentum since they are equal and opposite.

Applying the Conservation Law

The law of conservation of momentum can be expressed as:

EQUATION
—-----------------------------------------------------------------
Σp_before = Σp_after
Σp = total momentum (sum over all objects, considering direction)
—-----------------------------------------------------------------

This means that before and after an interaction, the vector total of momentum remains constant. This principle is vital in understanding both collisions (when objects strike each other) and separations (when objects move apart, such as in explosions).

For example:

• If two trolleys collide and stick together, their combined momentum after collision equals the total momentum before impact.

• In an explosion, fragments fly apart with momenta that add vectorially to zero if the system was initially at rest.

Collisions and Momentum Conservation

Collisions occur when two or more objects exert forces on each other for a short time.

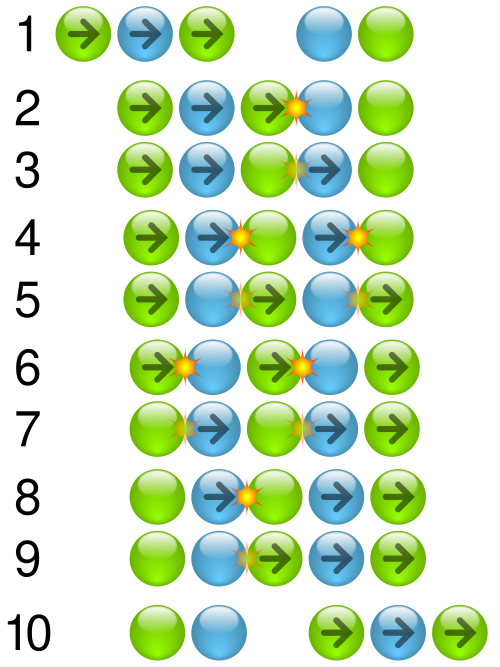
Diagram of a Newton’s cradle showing momentum transfer through successive balls in a near-elastic collision. It emphasises that total momentum of the system is conserved during the interaction. Note: the depiction also hints at elastic behaviour, which is extra detail beyond this OCR sub-subtopic but does not change the conservation message. Source

Regardless of whether kinetic energy is conserved (as in elastic collisions) or lost (as in inelastic collisions), momentum is always conserved in a closed system.

Types of Interactions

• Collision: Objects strike each other; they may bounce apart or stick together.

• Explosion: Objects start together and move apart due to internal forces.

• Separation event: Similar to an explosion but often involves slower processes, such as recoil or disintegration.

During any of these, Newton’s Third Law applies — for every action, there is an equal and opposite reaction — ensuring momentum exchange between interacting bodies is equal and opposite.

Newton’s Third Law and Momentum Exchange

When two bodies interact, they exert equal and opposite forces on each other for the same duration. The resulting impulses are equal in magnitude but opposite in direction, which guarantees that the total momentum of the system remains constant.

Thus, each body’s momentum changes, but these changes cancel when combined, leaving the total unchanged.

Vector Treatment of Momentum

Because momentum is a vector, both magnitude and direction must be considered in calculations. In one-dimensional cases, direction can be represented using positive and negative signs. In two- or three-dimensional systems, vector components are resolved along perpendicular axes, and the principle of conservation applies to each axis independently.

• Momentum is conserved separately in each direction (e.g. horizontal and vertical).

• Momentum diagrams can illustrate before-and-after states to visualise conservation.

• The resultant total momentum before and after must be equal when vectors are summed.

External Forces and System Boundaries

In real-world contexts, external forces can alter total system momentum. Examples include friction, drag, or a person pushing from outside the system. To apply the conservation principle accurately:

• Define clear system boundaries.

• Ensure external forces are negligible or balanced.

• Consider only internal interactions when calculating total momentum.

If external forces are not negligible, the rate of change of total momentum equals the net external force acting on the system, linking this principle to Newton’s Second Law.

Applications of Momentum Conservation

The conservation of momentum principle underpins a range of physical phenomena and technologies:

• Recoil in firearms: The forward momentum of the bullet is balanced by the backward momentum of the gun.

• Rocket propulsion: Expelling gas downwards gives the rocket upward momentum.

• Vehicle collisions: Engineers use momentum analysis to improve crash safety designs.

• Particle interactions: In nuclear and particle physics, momentum conservation is used to predict unseen particles or verify reaction outcomes.

In each case, total momentum before and after remains identical when viewed within a closed system.

Summary of Core Ideas for Application

To successfully apply the principle of conservation of momentum:

• Identify all objects involved and define the system.

• Write the total momentum before and after the event.

• Account for direction using sign conventions or vector components.

• Ignore external forces or treat them as negligible.

• Confirm total momentum before equals total momentum after.

These structured steps ensure consistent application of the conservation law in any collision or separation scenario, fulfilling the OCR specification requirement to apply the principle of conservation of momentum to closed systems during collisions or separations.