AP Syllabus focus:
‘Use the formal definition of continuity at x = c, requiring that f(c) exists, the limit of f(x) as x approaches c exists, and the limit equals f(c).’
A function’s continuity at a point provides a precise mathematical way to confirm that no breaks, jumps, or inconsistencies occur in its behavior as the input approaches a specified value.
The Need for a Formal Definition
The idea of a function being “unbroken’’ at a point becomes rigorous through a three-part test that connects function values with limit behavior. This structure ensures that continuity can be analyzed algebraically and interpreted consistently across graphs, formulas, and verbal descriptions, which is essential for developing deeper calculus concepts involving derivatives and integrals.
Understanding Continuity at a Point
The formal definition of continuity at a point establishes the exact relationship between a function’s value and its limiting behavior near that point. When considering a function f at a specific value c, this definition ensures that the function behaves predictably and smoothly as x approaches c.
Continuity at a Point: A function f is continuous at x = c if the following three conditions all hold: (1) f(c) exists, meaning the function has a defined value at c; (2) the limit exists; and (3) .
These conditions connect the function’s local behavior to its global structure and allow students to verify continuity in logically sequenced steps.
Condition 1: The Function Value Must Exist
The first requirement for continuity is that the function actually possesses a value at the point in question. Without a defined output, the function cannot be considered continuous because the foundation of comparison between value and limit collapses.
Why This Condition Matters
A missing point or hole in a graph prevents continuity, even if nearby values behave in a perfectly smooth way.
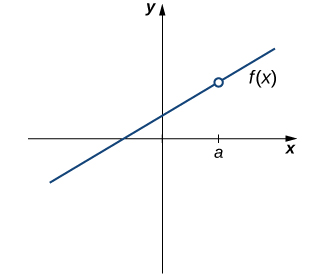
A graph showing a line with a single open circle at x=ax=ax=a, emphasizing that continuity requires the function value to exist at the point. The open circle marks a missing function value, illustrating failure of the first condition. Source.
Condition 2: The Limit Must Exist
The second requirement demands that the function’s behavior as x approaches c settles toward a single, finite value. This condition concerns nearby behavior, not the actual value of the function at c.
Key Features of Limit Existence
A limit exists when:
The left-hand limit and right-hand limit both exist and are equal.
The function does not oscillate or diverge as x approaches c.
The function approaches a single predictable value, even if the function is not defined at c itself.
This component ensures that the surrounding behavior behaves logically enough to support a stable value at the point.
Condition 3: The Limit Must Equal the Function Value
The final requirement establishes the connection between the limit and the actual function output. If the function value and the limit differ, continuity breaks because the function experiences a jump or mismatch at that location.
= Function describing the relationship between input and output
= Input value at which continuity is evaluated
A sentence between equation and next block prevents adjacency of structured elements.
Using the Three-Part Definition in Practice
To apply the formal definition, students typically verify each requirement in order. If any one of the three fails, the function is not continuous at that point. This structured approach allows for precise and systematic evaluation.
Checklist for Determining Continuity
Check whether the function value exists at x = c.
Look for defined outputs or identify missing or undefined points.Determine whether the limit exists.
Evaluate left- and right-hand behavior using numerical, graphical, or algebraic tools.Compare the limit to the function value.
If they match, the function satisfies the formal definition of continuity.
Common Situations Where Continuity Fails
A function may fail the continuity test in several recognizable ways, each corresponding to a failure of one or more of the three conditions.
Situations Where Condition 1 Fails
The function has an open circle or is not defined at c.
There is a break in the graph exactly at the point of interest.
Situations Where Condition 2 Fails
The left-hand and right-hand limits differ, leading to a jump discontinuity.
The function oscillates rapidly near the point.
The function approaches infinity, creating unbounded behavior.
Situations Where Condition 3 Fails
The function value is defined but does not equal the limit.
A removable discontinuity exists because the function value has not been set to match the limiting behavior.
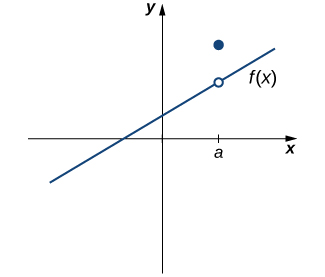
A graph where the limit value at x=ax=ax=a lies on the line, but the defined function value is a separate filled point above it. This mismatch demonstrates failure of the third continuity condition. Source.
The Importance of Formal Continuity in Calculus
The three-part definition serves as a foundational tool throughout calculus. Continuity guarantees predictable behavior required for the Intermediate Value Theorem, ensures differentiability in many contexts, and establishes a bridge between intuitive smoothness and rigorous mathematical analysis. Understanding this definition prepares students to reason precisely about functions and the dynamic processes they model.
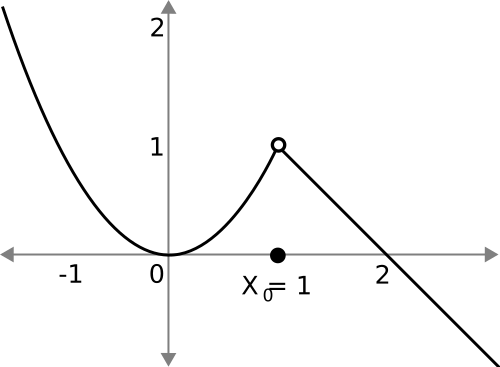
A clean curve with a hole marking a removable discontinuity, showing that although the limit exists, the function value is missing or mismatched. Redefining the point would restore continuity. Source.
FAQ
A frequent misconception is assuming that if a graph looks connected, the function must be continuous, even when the function value is undefined or mismatched at that point.
Another misconception is believing that the existence of a limit guarantees continuity, overlooking the need for the limit to equal the actual function value.
Students also often confuse continuity with differentiability, not realising that continuity is a weaker condition.
Use a structured approach:
• Check whether the function has an explicit definition at the point.
• Compute the limit from both sides using algebra.
• Compare the limit with the function value.
If all three align, the point is continuous. If any part fails, continuity is broken.
Continuity requires predictable behaviour as the input approaches the point from all directions. If the one-sided limits differ, the function exhibits a jump, meaning the nearby behaviour does not settle to a single value.
Even with a defined function value, mismatched one-sided limits break the logical link between limit behaviour and the point's output.
Yes. Piecewise functions can be continuous at a boundary if the pieces meet correctly.
This requires:
• Both pieces having the same limiting value at the boundary.
• The defined function value matching that same value.
The algebraic form may differ on each side, but continuity depends only on how they align at the joining point.
Absolutely. Many discontinuities arise when only one condition fails.
Examples include:
• The limit exists but the function value is missing (failure of condition 1).
• The function value exists but the limit does not (failure of condition 2).
• Both exist but do not match (failure of condition 3).
Continuity requires all three conditions simultaneously, so any single failure is enough to break continuity.
Practice Questions
Question 1 (1–3 marks)
A function f is defined for all real numbers except at x = 2. The limit of f(x) as x approaches 2 exists and equals 5. The value of f(2) is not defined.
(a) Determine whether f is continuous at x = 2.
(b) Give a reason for your answer, referring to the formal three-part definition of continuity.
Question 1
(a) 1 mark
• f is not continuous at x = 2.
(b) 2 marks
• 1 mark: States that continuity requires the function value to exist, the limit to exist, and the limit to equal the function value.
• 1 mark: Explains that f(2) does not exist, so the first condition of continuity fails even though the limit exists.
Total: 3 marks
Question 2 (4–6 marks)
A function g is defined as follows:
g(x) = x + 3 for x ≠ 1
g(1) = 10
(a) Find the limit of g(x) as x approaches 1.
(b) State the value of g(1).
(c) Using the formal definition of continuity at a point, determine whether g is continuous at x = 1.
(d) Explain clearly which of the three conditions for continuity fails, showing full reasoning.
Question 2
(a) 1 mark
• Correct limit: 4.
(b) 1 mark
• States g(1) = 10.
(c) 1 mark
• Concludes that g is not continuous at x = 1.
(d) 2–3 marks
• 1 mark: Identifies that although the limit exists, it does not equal the function value.
• 1 mark: Correctly references the three-part continuity definition.
• 1 mark (only if fully justified): Clearly states that the third condition fails because the limit (4) does not equal g(1) (10).
Total: 5–6 marks

