Continuity at a point describes when a function’s graph flows smoothly without breaks or sudden jumps. Understanding this intuitive idea builds the foundation for later formal limit-based definitions.

The Intuitive Meaning of Continuity at a Point

Continuity begins with the visual idea that a function behaves smoothly at a specific value of x, without interruptions or abrupt changes. When students first encounter continuity, the image of drawing a graph without lifting the pencil offers a powerful way to understand how functions behave near a point.

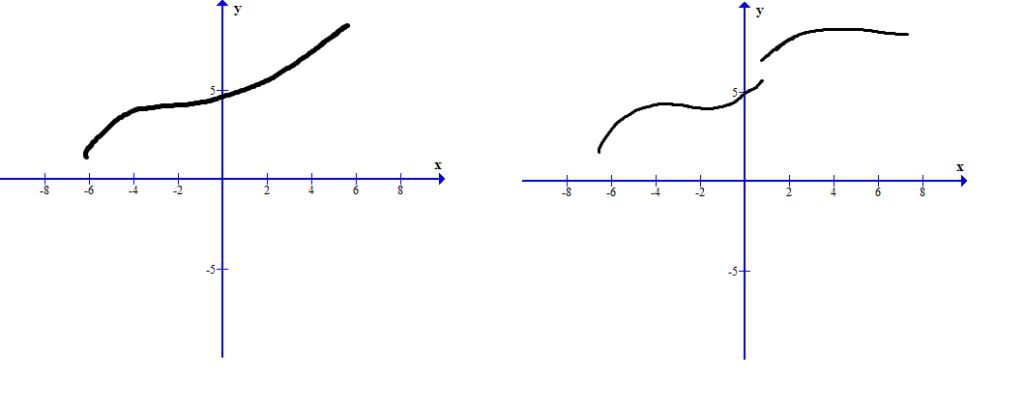
Two graphs compare a continuous function with one that has a jump discontinuity. The continuous graph can be traced without lifting a pencil, illustrating the intuitive meaning of continuity. The image highlights how a break or jump disrupts the expected local behavior of a function. Source.

This intuitive perspective emphasizes what the function looks like and how it behaves locally, rather than relying immediately on formal limit notation. The AP syllabus stresses viewing continuity as the absence of breaks or jumps, then connecting that understanding to deeper limit-based reasoning.

Smooth, Predictable Local Behavior

A function is continuous at a point when its nearby values align naturally with the function’s value at that point. In other words, as x approaches a specific value, the function’s output moves in a predictable manner rather than shifting suddenly. This idea forms the bridge between graphical intuition and calculus concepts that depend on smoothness, such as differentiation.

When a graph shows no holes or jumps at a point, we typically say it is “continuous there” because the local behavior of the function matches what is expected from the surrounding parts of the graph. This connection between visual smoothness and local predictability is fundamental to understanding continuity across all contexts.

Connecting Intuition to the Behavior of Limits

Although this subsubtopic focuses on intuition, the idea of limits naturally arises when describing how a function behaves as x gets close to a certain value. The notion that the function’s values approach a single, stable number reinforces the concept of graphical smoothness. This prepares students for the three-part formal definition that appears later in the course, where limits become the core analytical tool for determining continuity.

Between the intuitive picture and its limit-based explanation lies the recognition that continuity reflects the agreement between what happens at the point and what happens close to that point.

Understanding Breaks, Jumps, and Holes through Intuition

Students should be able to identify discontinuities visually before working with algebraic tools. The intuitive notion of continuity highlights three types of disrupted behavior:

• Breaks: The graph ends or pauses before resuming elsewhere, signaling that the function does not provide a value that fits smoothly with surrounding values.

• Jumps: The graph shifts suddenly from one height to another, creating a visible vertical gap reflecting inconsistent behavior near the point.

• Holes: The function approaches a value but is missing the actual point, creating a removable discontinuity that is intuitively clear from the graph.

Each of these disruptions represents a failure of the graph to follow a single, predictable path through the point of interest.

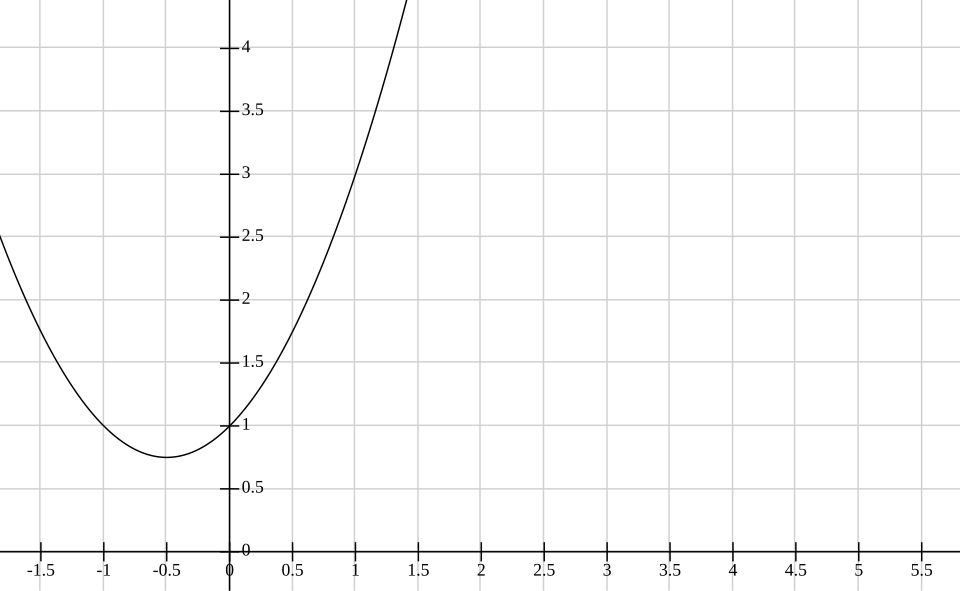
This graph depicts a smooth curve with a single hole, where the function is not defined at one point despite approaching a clear value nearby. It visually illustrates a removable discontinuity. The formula shown in the image exceeds syllabus needs but does not detract from its usefulness in representing a hole at a specific point. Source.

Students should recognize that continuity is lost whenever the function’s behavior cannot be drawn smoothly at that location.

Why Intuition Matters Before Formalism

Before introducing formal continuity conditions, students benefit from building strong visual and conceptual intuition. This conceptual readiness helps prevent confusion later when limits and symbolic definitions become central. When learners already associate continuity with smooth, unbroken behavior, they can more easily interpret what the limit is doing and how a function value must match it.

This intuitive grounding also helps students evaluate real-world models, where continuity captures the idea that physical quantities change gradually rather than instantaneously leaping between values.

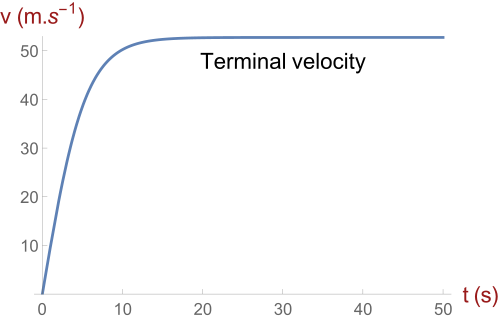
This real-world graph shows a skydiver’s velocity increasing smoothly over time with no jumps, demonstrating continuity in physical motion. The curve approaches terminal velocity gradually. Although the image includes a specific analytic model, students need only focus on its continuous shape. Source.

When students recognize why engineers, scientists, and economists depend on continuous models, they gain a deeper appreciation for the concept’s significance.

Developing a Mental Checklist for Intuitive Continuity

Even before the formal definition is introduced, students can use a simple mental process to judge intuitive continuity at a point:

• Look for unbroken behavior in the graph near the point.

• Check whether the graph can be drawn smoothly through the point.

• Notice whether any value is missing even though the rest of the graph approaches a particular height.

• Observe whether the graph jumps to a different height without passing through the intermediate region.

• Decide whether the surrounding behavior matches the function’s value at the point.

This checklist aligns closely with the later formal requirements, but focuses first on visual and conceptual clarity. By establishing these habits early, students develop more robust reasoning that will support later analytical work with limits.

Building Toward the Formal Definition

Although this page does not present the formal three-part definition in full, students must understand that intuitive continuity prepares them for it. The idea that the function’s value matches what the function “wants to be” based on nearby inputs directly leads into evaluating limits at a point. This intuition reinforces the future emphasis on checking whether a limit exists and whether it corresponds to the function’s stated value.