AP Syllabus focus:
‘Recognize composite functions and identify their inner and outer functions so you can decide when the chain rule is needed to simplify differentiation.’
Recognizing composite functions is essential for identifying when differentiation requires layered reasoning. These notes introduce how to detect compositions by distinguishing inner and outer functions across a wide range of expressions.
What Composite Functions Are
A composite function arises when one function is applied inside another, producing a nested structure that requires careful unpacking during differentiation.
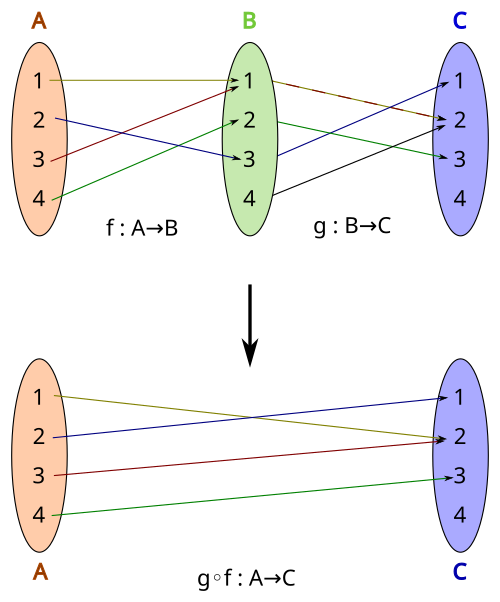
This diagram illustrates two functions, and , mapping between sets, with the composite mapping showing how outputs of one function become inputs to another. It emphasizes the structure of functional composition. The abstract sets introduce generality beyond AP Calculus AB but remain fully aligned with the concept of composition. Source.
Composite Function: A function created when one function is inserted into another, expressed symbolically as .
Composite functions matter because the structure—not just the appearance—of an expression determines the correct differentiation procedure. You must examine how functions are built, not just how they look.
Identifying Inner and Outer Functions
The ability to find the inner function and outer function is central to recognizing when a function is composite. The outer function is the final operation applied to the input, while the inner function is the expression inside that provides the input to the outer layer.
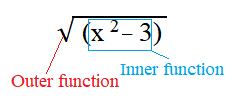
This diagram identifies the square root as the outer function and the expression as the inner function, illustrating clearly how mathematical layers form a composite function. The simple color-coded labels reinforce the concept without introducing unnecessary complexity. The example aligns directly with AP expectations for recognizing inner and outer structures. Source.
Outer Function: The overarching function applied last in a composition, dictating the global operation performed on the inner function.
A sentence must exist between definition blocks to maintain proper separation.
Inner Function: The function nested inside another function whose value becomes the input to the outer function.
Understanding which part of an expression is “inside” another helps determine whether the chain rule is necessary. Students should view functions as layers, much like nested containers, each representing a different mathematical operation.
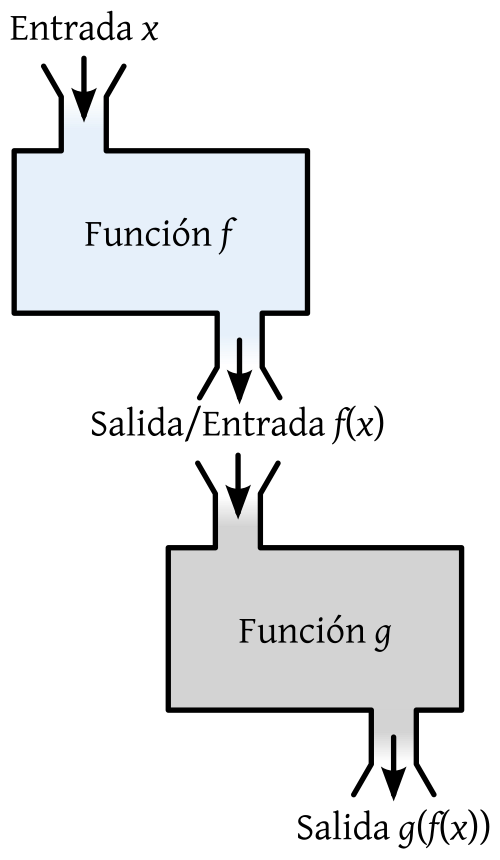
This visual represents composition as sequential processing through two function machines, reinforcing the idea of layered operations. It highlights how an input is transformed step-by-step through nested functions. While general in style, it supports the AP focus on structural understanding of compositions. Source.
Key Characteristics of Composite Functions
Recognizing a composite function often involves noticing clues within the structure of a function. Important indicators include:
• An expression placed inside parentheses, brackets, radicals, or exponents.
• A trigonometric, exponential, or logarithmic function acting on a non-trivial expression.
• A complicated inner structure modified by an additional operation.
• A layered dependency where the value of one function feeds directly into another.
These indicators signal a nested configuration that cannot be differentiated with a single basic rule.
Why Recognizing Composition Matters for Differentiation
Differentiation rules operate based on structure. When faced with a composite function, the chain rule becomes essential because it differentiates functions in layers. Misidentifying composition often leads to incorrect derivatives, especially when students assume an inner expression is independent or incorrectly apply a simpler rule.
Even though the chain rule itself belongs to later subsubtopics, the ability to recognize composite functions is foundational. Before applying any rule, students must determine whether the expression is a simple function, a product or quotient, or a composition requiring layered differentiation.
Structural Cues in Common Function Families
Composite functions appear frequently in standard families encountered in AP Calculus AB. Recognizing these recurring structures improves accuracy and confidence when differentiating.
Polynomial-Based Composites
Many polynomial expressions become composite when a polynomial is placed inside another function, especially when wrapped by powers, roots, or absolute values. Students should scan for:
• Non-linear expressions inside radicals or exponents
• Polynomial arguments of trigonometric or exponential functions
• Absolute values applied to algebraic expressions
Trigonometric Composites
Trigonometric functions often create composite structures when the input is anything other than a single variable. Look for:
• Sine, cosine, tangent, or other trig functions applied to algebraic or transcendental expressions
• Nested trig functions, indicating more than one functional layer
• Trigonometric identities that hide composition within transformed expressions
Exponential and Logarithmic Composites
Exponential and logarithmic functions frequently contain compositions because their arguments are rarely simple constants or single variables in calculus contexts. Signals include:
• Variable inputs raised to powers inside exponentials
• Logarithmic functions applied to expressions containing products or sums
• Arguments containing nested functions such as trig or rational expressions
How to Deconstruct a Function into Inner and Outer Components
To determine whether a function is composite, use a systematic approach:
• Identify the final operation performed on the expression; this is the outer function.
• Examine what that outer function takes as its input; this input is the inner function.
• Check whether the inner function itself contains additional layers; if so, the composition may involve multiple levels.
• Confirm whether the structure indicates chained operations rather than separate, simultaneous ones.
Common Misconceptions When Identifying Composite Functions
Students sometimes overlook composite structures because they focus on symbolic complexity rather than functional layering. Key misconceptions include:
• Assuming parentheses always represent multiplication, ignoring their frequent role in nesting functions.
• Treating inner expressions as independent variables, which leads to misapplied differentiation rules.
• Confusing products or sums of functions with compositions; composite functions require insertion, not mere combination.
A strong conceptual understanding of how functions nest ensures that later differentiation steps follow logically and correctly.
Developing Fluency Through Structural Awareness
Recognizing composite functions is a skill built through repeated exposure and careful attention to mathematical structure. Students should develop a habit of visually parsing expressions to identify operational layers. This structural awareness equips them to determine when the chain rule is needed, aligning directly with the AP requirement to recognize composite functions and correctly identify their inner and outer components.
FAQ
Check whether one expression is being fed entirely into another, rather than two expressions being combined.
A composite function requires functional nesting, whereas products and sums simply combine values side by side.
Look for:
• A whole expression inside parentheses, radicals, or function notation.
• A final operation applied to a full expression rather than to individual terms.
The final operation determines the outer function, which sets the structure for how the function is built.
Understanding the outermost layer prevents misclassification, especially when several operations appear together.
A good strategy is to imagine “peeling back” layers by asking:
• What operation is performed last?
• What expression is this operation acting on?
Yes, when a function has multiple nested layers, different decompositions may be valid depending on the analytical purpose.
For example, you may choose:
• A deeply nested expression as the inner function for structural clarity.
• A simpler sub-expression as the inner function when preparing to differentiate.
The key is that the chosen inner function must be wholly contained within the outer function.
Some algebraic expressions hide their compositional nature because formatting makes the nesting subtle. Powers, roots, and absolute values often conceal an inner structure.
To reveal composition, rewrite the expression using explicit function notation or brackets. This can expose a layer that was visually understated.
Common errors include:
• Choosing the first operation seen rather than the last operation applied.
• Confusing algebraic simplification with functional structure.
• Treating coefficients as part of the outer function rather than the inner expression.
Avoid these by focusing on the order in which the expression is built, not how it is written.
Practice Questions
Question 1 (1–3 marks)
Consider the function h(x) = sin(3x + 1).
(a) State the outer function.
(b) State the inner function.
Question 1
(a) Outer function: sin(x).
• 1 mark for correctly identifying sin(x) as the outer function.
(b) Inner function: 3x + 1.
• 1 mark for correctly identifying 3x + 1 as the inner function.
Award full 2 marks only if both inner and outer functions are correctly identified.
Question 2 (4–6 marks)
A function is defined by f(x) = ln(5x^2 − 4).
(a) Explain why f is a composite function.
(b) Identify the inner and outer functions.
(c) A student claims that f can be differentiated using only the derivative of ln(x). Explain why this is incorrect, referring to the structure of the function.
(a) Explanation: f is composite because the logarithm function operates on an expression (5x^2 − 4) rather than directly on x.
• 1 mark for noting that the input to ln is not simply x.
• 1 mark for stating that one function is applied inside another.
(b) Inner function: 5x^2 − 4.
Outer function: ln(x).
• 1 mark for each correctly identified function (2 marks total).
(c) Explanation: The derivative of ln(x) alone is insufficient because the argument of the logarithm is itself a function of x; therefore, the chain rule is required.
• 1 mark for identifying that the inner function changes the differentiation process.
• 1 mark for explicitly stating that the chain rule is needed due to the composite structure.
Total: 6 marks.

