Preparing trigonometric expressions before differentiating helps simplify structure, reduce algebraic complexity, and ensure accurate application of derivative rules using identities that rewrite functions into more manageable equivalent forms.

Using Identities to Prepare Trig Functions for Differentiation

Before applying derivative rules, AP Calculus AB students must recognize that many trigonometric expressions are easier to differentiate when rewritten using trigonometric identities. These identities reveal equivalent forms that align naturally with known derivatives of sine, cosine, and basic reciprocal functions.

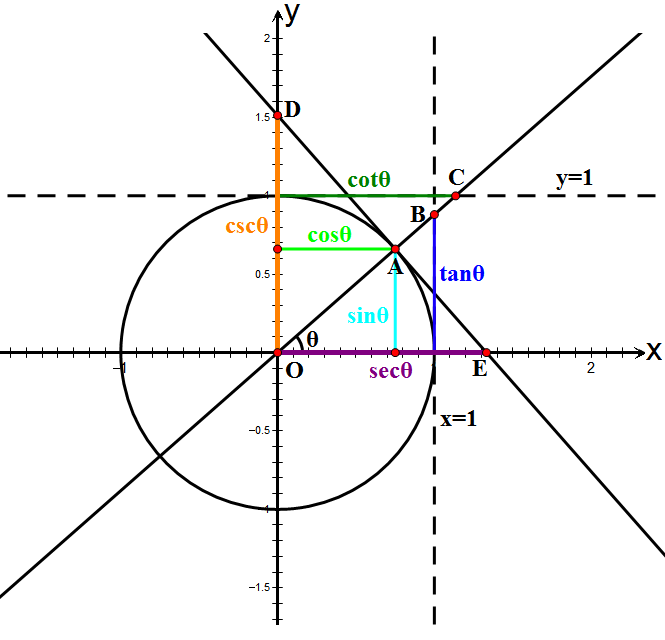
This diagram illustrates how the six trigonometric functions of an angle $\theta$—$\sin$, $\cos$, $\tan$, $\cot$, $\sec$, and $\csc$—are defined using segments on the unit circle. It highlights that reciprocal and quotient relationships arise naturally from the geometry, supporting the strategy of rewriting functions in terms of $\sin$ and $\cos$. The figure contains additional geometric detail not required in the AP syllabus. Source.

It visually connects each function and its reciprocal to coordinates or line segments, reinforcing the idea that they are different “views” of the same underlying geometry. Rewriting an expression is not algebraic busywork; it is a strategic step that prevents errors, highlights structure, and supports more efficient differentiation.

Fundamental Strategy: Rewrite Before Differentiating

The guiding principle is to express a trigonometric function in a form that makes its derivative straightforward. Students should look for opportunities to transform complicated products, quotients, or compositions into expressions involving elementary trig functions whose derivatives are familiar.

Common objectives include:

• Converting reciprocal or quotient-based trigonometric functions into sine–cosine forms.

• Using Pythagorean identities to replace squared or composite expressions.

• Restructuring expressions to make the product rule, quotient rule, or chain rule cleaner to apply.

Core Trigonometric Identities Used in Differentiation

When preparing an expression for differentiation, several identities recurrently streamline the process. They allow a function to be rewritten without changing its value while significantly reducing derivative complexity.

A brief list of highly useful identities for this subsubtopic includes:

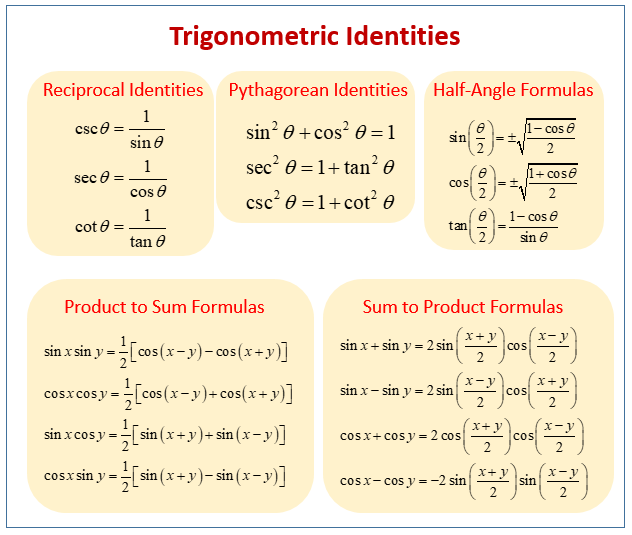
This chart summarizes key trigonometric identities, including the reciprocal and Pythagorean identities essential for rewriting $\tan$, $\cot$, $\sec$, and $\csc$ in terms of $\sin$ and $\cos$. Its structured layout highlights relationships used to prepare expressions before differentiating. The image contains extra formulas (e.g., half-angle and product-sum identities) not required for this AP subsubtopic. Source.

• Reciprocal identities

  • $\sec x = 1/\cos x$

  • $\csc x = 1/\sin x$

  • $\tan x = \sin x/\cos x$

  • $\cot x = \cos x/\sin x$

• Pythagorean identity

  • $\tan^{2}x + 1 = \sec^{2}x$

• Other rearrangements

  • $\cot x = 1/\tan x$

  • $\sec x = \tan x \csc x$ (in certain contexts)

These identities do not yet require differentiation; instead, they prepare the function so that standard rules become easier to apply.

Why Rewriting Helps When Applying Derivative Rules

Many derivative errors originate from applying rules to functions in unnecessarily complicated forms. Rewriting resolves this by clarifying functional structure.

Key advantages include:

• Revealing hidden products or quotients, enabling correct use of product or quotient rules.

• Transforming unfamiliar composite expressions into forms built from basic trig functions, whose derivatives are already memorized.

• Minimizing algebraic manipulation after differentiation.

Product Rule and Quotient Rule Readiness

Because tangent, cotangent, secant, and cosecant frequently appear in combinations, preparing them properly avoids misidentifying functional relationships.

A normal sentence is included here to maintain required spacing before the next definition.

Once a function is explicitly written as a quotient, students can confidently apply derivative procedures without guessing about the underlying structure.

Using Sine–Cosine Forms to Simplify Derivatives

Rewriting every tangent, cotangent, secant, or cosecant expression in terms of sine and cosine is often the single most effective preparation technique.

Benefits of sine–cosine rewriting:

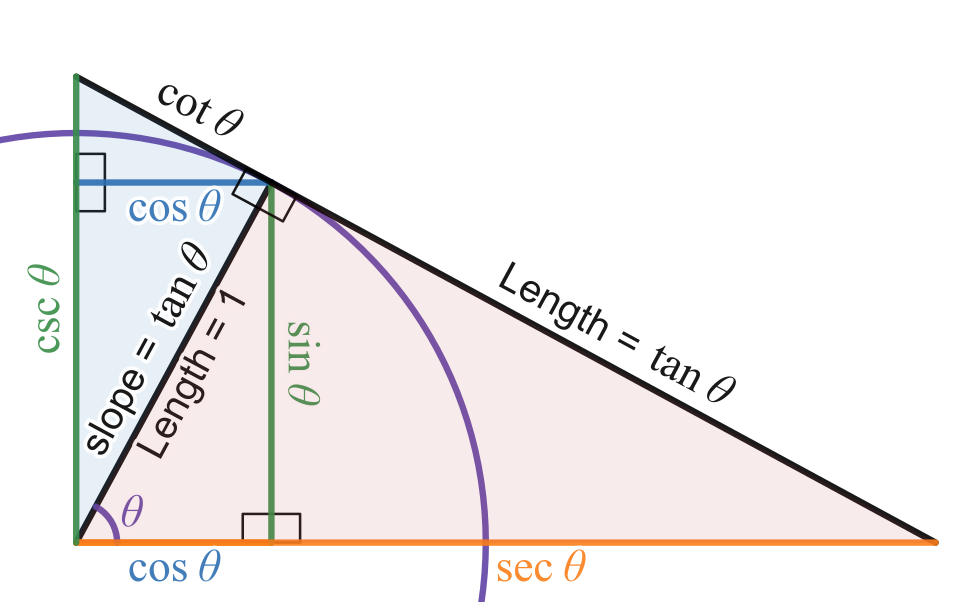
This diagram shows how each trigonometric function and its reciprocal correspond to specific geometric line segments for the same angle $\theta$. Viewing reciprocal pairs together reinforces why identities like $\tan\theta = \frac{\sin\theta}{\cos\theta}$ and $\sec\theta = \frac{1}{\cos\theta}$ hold. The color-coding and additional labeling provide more detail than required in the AP syllabus but clarify how identities guide algebraic rewriting. Source.

• Only $\sin x$ and $\cos x$ are primary trig functions, and their derivatives are well known.

• Algebraic simplification becomes more predictable when dealing with standard functions.

• The resulting expressions integrate seamlessly with rules for products, quotients, and chains.

When to Apply Identities Before Differentiating

Students should deliberately choose to rewrite using identities when:

• The original form obscures whether a product or quotient rule is required.

• The function contains reciprocal trig expressions that become cleaner in sine–cosine form.

• An identity converts a multi-layered composition into a simpler equivalent.

• Squared or higher-order trig expressions produce more manageable derivatives when replaced using Pythagorean identities.

Process for Preparing Trig Expressions

A structured approach promotes consistency and accuracy:

• Identify the trigonometric expressions that may complicate differentiation.

• Select an appropriate identity based on whether the expression can be rewritten as a product, quotient, or simpler function.

• Rewrite using sine, cosine, or relevant identities.

• Confirm functional structure (product, quotient, or basic function).

• Proceed with differentiation rules once the expression is in its clearest form.

Efficiency and Correctness Through Identity Use

Using identities before differentiating is not optional refinement; it is an essential skill that ensures alignment with AP Calculus AB expectations. These identity-based rearrangements promote mathematical clarity, highlight inherent relationships among trig functions, and enhance the precision of derivative calculations.