AP Syllabus focus:
“Use derivative values to describe how a quantity is changing at an instant in applied problems, clearly stating what is changing, how fast it is changing, and in which units.”
Understanding derivative values in real situations allows us to describe instantaneous change precisely, linking mathematical ideas to meaningful contexts where quantities shift over time or in response to another variable.
Interpreting Derivative Values in Context
Interpreting a derivative in an applied setting centers on translating symbolic information into precise verbal statements about how a specific quantity is changing at a specific instant.
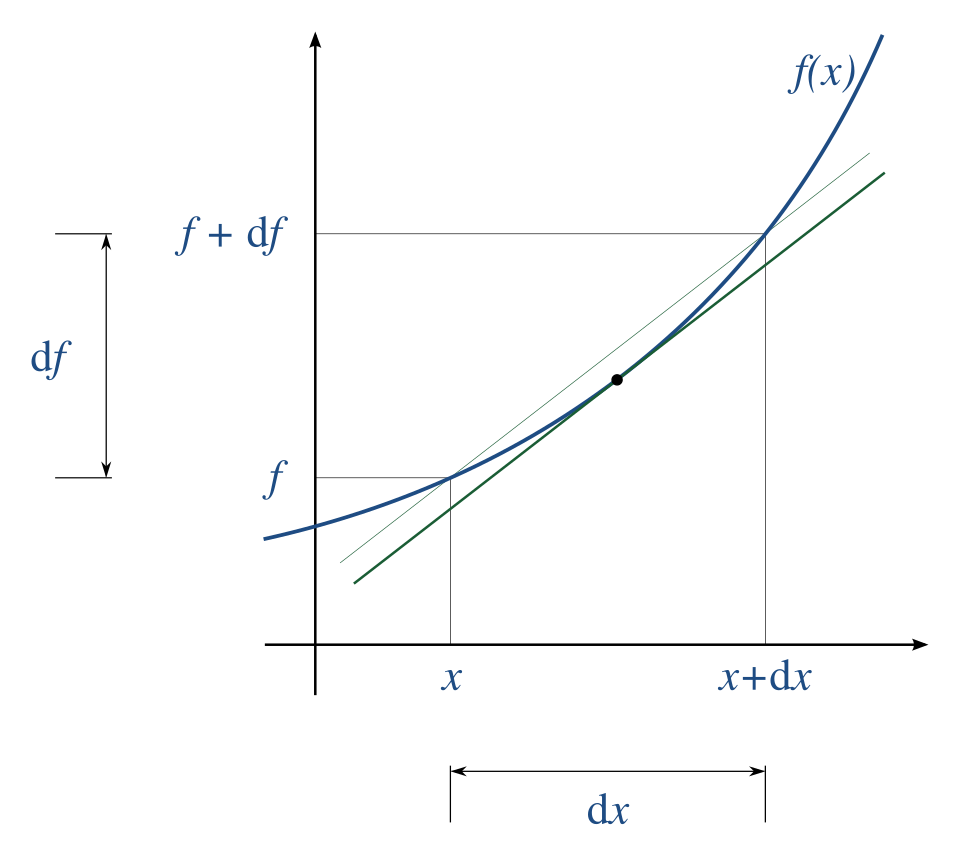
This figure shows a curve with a tangent line drawn at a point, illustrating that the derivative at that point equals the tangent line’s slope. The slope represents the instantaneous rate at which the output changes with respect to the input. The graphic focuses on slope rather than units, so you must still supply units from the problem context when interpreting a derivative value. Source.
The goal is to articulate what is changing, how quickly it is changing, and the units that describe that rate.
Identifying the Quantity That Is Changing
The dependent variable is the quantity whose instantaneous rate of change is represented by the derivative. When interpreting a derivative value, the first step is recognizing which real-world measurement corresponds to this variable.
Dependent Variable: The quantity whose value depends on the input and whose instantaneous rate of change is given by the derivative.
After identifying the dependent variable, the next requirement is to express clearly how this variable behaves at the given instant. This means avoiding vague statements and instead giving explicit descriptions that capture the real situation.
Understanding Instantaneous Change
The derivative value tells how the dependent variable changes with respect to the independent variable, most commonly time but potentially another contextual variable such as temperature, cost, distance, or volume.
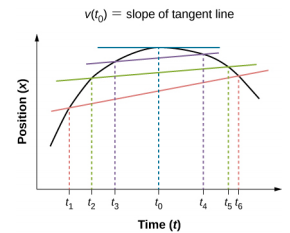
This position–time graph shows several secant slopes approaching the tangent slope at a specific time, emphasizing that the tangent slope represents the instantaneous velocity. The sign of the slope indicates direction, while the magnitude indicates how fast position is changing at that instant. The extra secant-line comparisons go slightly beyond the minimum needed for interpretation, but they reinforce what “instantaneous” means. Source.
Instantaneous Rate of Change: The rate at which a quantity is changing at a specific moment, represented by the value of the derivative at that point.
Because instantaneous change concerns a single moment, it differs fundamentally from average change over an interval. Here, the emphasis is on describing what happens “right now,” reflecting the most immediate behavior of the function.
Interpreting the Sign of the Derivative
The sign of the derivative plays a key role in contextual interpretation. It provides insight into the direction of change, signaling whether the dependent variable is increasing or decreasing at the moment of interest. When interpreting the sign, connect the mathematical result directly to the real-world context.
Key points include:
A positive derivative indicates the quantity is increasing with respect to the input variable.
A negative derivative indicates the quantity is decreasing with respect to the input variable.
A derivative equal to zero indicates no instantaneous change at that moment, which might signify a temporary maximum, minimum, or plateau.
These interpretations must always tie back to the specific situation, such as height rising over time, temperature dropping as altitude increases, or cost remaining momentarily unchanged.
Interpreting the Magnitude of the Derivative
The magnitude tells how fast the quantity is changing. It measures the strength or intensity of change, and interpreting it requires recognizing what the numerical value represents relative to the context.
Students should:
Identify the size of the instantaneous effect.
Understand whether the magnitude suggests rapid or slow change.
Relate the size to meaningful reference points, such as typical growth rates or everyday speeds, without performing numerical comparisons.
The magnitude alone is insufficient; it must be paired with the dependent and independent variables to form a fully correct interpretation.
Using Units in Derivative Interpretation
Units are essential for communicating meaning. Because a derivative represents a ratio of changes, its units combine those of the dependent and independent variables. Failure to include units weakens the interpretation and obscures the real-world meaning.
Derivative Units: The compound units formed by dividing the units of the dependent variable by the units of the independent variable.
Between definition blocks, it is important to note that correct unit interpretation provides clarity and prevents common misunderstandings about what the derivative measures.
A well-structured interpretation always contains:
The name of the changing quantity.
The direction of change (increasing or decreasing).
The rate at which it is changing (magnitude and sign).
The appropriate compound units derived from the context.
Constructing a Complete Interpretation Statement
A complete interpretation transforms a derivative value into a contextual sentence. This statement must accurately reflect the meaning of the derivative without introducing conclusions that the derivative does not support. A strong interpretation typically includes the following:
Specify the dependent variable and describe it clearly.
State the rate of change, including sign and magnitude.
Include the independent variable to clarify the frame of reference.
Express the interpretation in units, ensuring mathematical and contextual precision.
Anchor the description to the instant at which the derivative is evaluated.
Avoiding Common Interpretation Errors
Students should be aware of frequent misinterpretations that can distort the meaning of a derivative value:
Confusing instantaneous rate with average rate.
Omitting units, which removes essential context.
Misreading the sign, especially in cases where the real-world quantity might not behave intuitively.
Failing to specify the instant at which the derivative is taken.
Giving interpretations suggesting long-term behavior or predictions not supported by instantaneous information.
Carefully distinguishing what the derivative does and does not tell us ensures interpretations remain mathematically valid and contextually accurate, aligning with the AP expectation of “clearly stating what is changing, how fast it is changing, and in which units.”
FAQ
Always identify what the input variable represents in the real situation. If the variable measures time, the derivative gives a rate per unit time.
If the input measures something else, such as temperature, distance, cost, or volume, then the derivative describes how the dependent variable changes per unit of that quantity instead.
Check the problem statement carefully, as the correct interpretation depends entirely on the meaning of the independent variable.
A clear interpretation typically includes:
• The dependent variable
• Whether it is increasing or decreasing
• The instantaneous rate of change
• The units
• The specific instant at which the value applies
A concise structure is: “At [input value], the [dependent variable] is [increasing/decreasing] at a rate of [derivative value] [units].”
If the input or output uses composite units, the derivative’s units simply combine them as a ratio.
For example:
• Output in grams per square metre and input in hours gives a rate in grams per square metre per hour.
• Output in revenue per day and input in number of customers gives a rate of revenue per day per customer.
If units seem confusing, rewrite each quantity as “units of output per units of input” to clarify the meaning.
The mathematical value gives the speed of change, but practical significance depends on context.
To evaluate significance:
• Compare the rate to typical or expected behaviour in that situation.
• Consider whether the rate would noticeably affect the system over short time intervals.
• Think about the variability of the quantity: a change of 5 units may matter greatly in one context but be negligible in another.
Always judge significance relative to the real-world scale of the dependent variable.
A negative derivative does not imply the quantity becomes negative; it only indicates the direction of change.
If the dependent variable cannot fall below zero (such as population, mass, or area), then a negative derivative means the quantity is decreasing at that instant.
Check whether the decrease is reasonable within the context. In constrained situations, a negative derivative may signal a decline toward a minimum value rather than an indefinite continuation of the trend.
Practice Questions
Question 1 (1–3 marks)
A tank contains V litres of water, where V is a differentiable function of time t, measured in minutes. At a particular instant, the derivative V'(t) is equal to -2.3.
Interpret the value -2.3 in the context of the situation, clearly stating what is changing, how fast it is changing, and in which units.
Question 1 (1–3 marks)
• 1 mark for identifying the quantity that is changing (the volume of water in the tank).
• 1 mark for stating the rate correctly (decreasing at 2.3 litres per minute).
• 1 mark for including correct units and stating that the interpretation applies at that instant.
Maximum: 3 marks.
Question 2 (4–6 marks)
A population of insects is modelled by a differentiable function P(t), where t is the time in days. The derivative P'(t) gives the instantaneous rate of change of the population.
At t = 5, the value of P'(5) is 120, and the value of P(5) is 800.
(a) Interpret the value P'(5) = 120 in context.
(b) Explain what the sign of P'(5) indicates about the population at t = 5.
(c) A student claims that because P'(5) = 120, the population must increase by 120 insects every day for the next week. Explain why this conclusion is not justified.
Question 2 (4–6 marks)
(a) Interpretation of P'(5) = 120 (2 marks)
• 1 mark for correctly identifying the dependent variable (the insect population).
• 1 mark for stating that at t = 5 days the population is increasing at a rate of 120 insects per day.
(b) Explanation of the sign (1 mark)
• 1 mark for stating that the positive sign means the population is increasing at that instant.
(c) Explanation of why the conclusion is not justified (2–3 marks)
• 1 mark for stating that the derivative gives an instantaneous rate, not an average or long-term rate.
• 1 mark for explaining that P'(t) may change over time, so the rate is not necessarily constant.
• 1 additional mark for clarity, such as noting that the derivative only applies precisely at t = 5.
Maximum: 6 marks.

