AP Syllabus focus:
‘Understand that the derivative of a function at a point represents the instantaneous rate of change of the dependent variable with respect to its independent variable in a given context.’
Understanding Derivatives as Instantaneous Rates of Change
The derivative provides a precise mathematical tool for describing how one quantity changes at an exact moment, allowing us to model rapidly evolving real-world behaviors with clarity.
The Idea of Instantaneous Change
In many contexts, quantities vary continuously, and understanding their behavior at a single moment is essential. The instantaneous rate of change captures this idea by measuring how fast a dependent variable changes with respect to an independent variable at a specific point. Students often first encounter change through average rates, but instantaneous rates refine this understanding to a single, exact instant.
When discussing the derivative in context, the dependent variable is the quantity whose behavior we observe, while the independent variable is the one with respect to which change is measured. The derivative links them by describing how sensitive the dependent variable is to small changes in the independent variable.
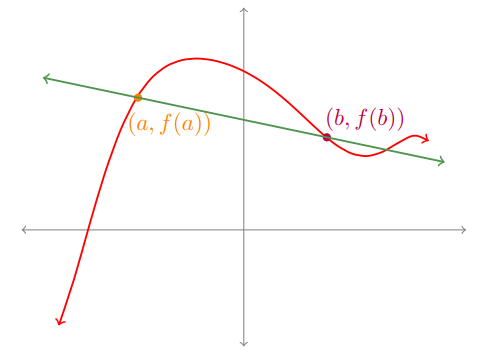
A smooth curve is shown with a single tangent line touching it at one point. The slope of this tangent line illustrates the instantaneous rate of change at that location. The diagram focuses solely on the geometric meaning of the derivative without introducing extra concepts. Source.
Term: Instantaneous rate of change — The rate at which a quantity is changing at a single point, found using the derivative of the function describing that quantity.
Before moving to formal notation, it is useful to emphasize that instantaneous rates appear in many applied settings, such as growth processes, movement, and changing measurements in physical systems.
Derivatives as Measures of Sensitivity
The derivative not only captures speed of change but also communicates direction, distinguishing increases from decreases. A positive derivative signifies that the dependent variable is increasing with the independent variable, while a negative derivative indicates a decreasing trend. A derivative of zero reflects a momentary pause in change, often associated with peaks, troughs, or other critical moments in an applied scenario.
= Instantaneous rate of change of the function at input
= Value of the function (units depend on context)
= Small change in the input variable
This limit-based formula formalizes the derivative, but in applied interpretation, the emphasis lies in what the derivative means for the situation being modeled. Students must always relate back to the units and quantities involved.
Interpreting Instantaneous Rates in Context
When using derivatives in real-world scenarios, interpretation is central. A derivative always answers three questions:
• What quantity is changing?
• How fast is it changing?
• With respect to which variable is the change occurring?
These components ensure that interpretations remain tied to the situation rather than becoming purely symbolic calculations.
Term: Dependent variable — The quantity whose value depends on changes in another variable within a given context.
A clear interpretation must state not only that a quantity is increasing or decreasing but also provide the correct units. For example, if measures height in meters and represents time in seconds, then has units of meters per second, matching the meaning of “rate of change of height with respect to time.”
Distinguishing Instantaneous and Average Rates
Although both describe change, an average rate of change summarizes behavior over an interval, whereas an instantaneous rate focuses on a single moment. In applied problems, students must recognize that the derivative represents behavior that may differ significantly from the average trend when conditions change rapidly. This distinction ensures accurate modeling in contexts where immediate behavior matters.
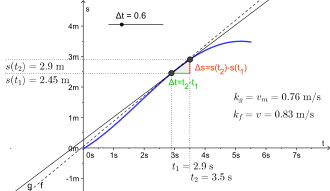
The graph shows a curve with several secant lines and one tangent line, illustrating the difference between average and instantaneous rates of change. The slope of each secant represents an average rate, while the tangent’s slope gives the instantaneous rate at a specific moment. The inclusion of average velocity labels provides helpful context without extending beyond the core concept of instantaneous change. Source.
A normal sentence here reinforces how important it is to anchor interpretations in the problem’s narrative rather than rely solely on mathematical expressions.
Why Instantaneous Rates Matter
Instantaneous rates appear across scientific, economic, biological, and physical systems, making the derivative an essential conceptual tool. Some key features include:
• Precision: Allows measurement of change at a specific moment rather than across a span.
• Predictive power: Helps anticipate near-future behavior by identifying how quantities evolve locally.
• Contextual clarity: Ensures that modeling remains faithful to the real situation.
Term: Derivative at a point — The instantaneous rate of change of a function with respect to its input variable at an exact value of that input.
A final normal sentence clarifies that mastering instantaneous rates of change equips students to interpret and analyze dynamic processes with mathematical accuracy.
FAQ
In practice, instruments approximate instantaneous rates by sampling data at extremely small time or distance intervals. The smaller the interval, the closer the measured rate comes to the true instantaneous rate.
Devices such as speedometers, heart-rate monitors, and environmental sensors all rely on rapidly updated average rates that serve as practical stand-ins for instantaneous change.
An average rate blends information over an interval, so short-lived fluctuations are concealed. The derivative isolates the behaviour at a single moment, revealing changes that might otherwise be hidden.
This precision is crucial in contexts where rapid shifts occur, such as chemical reactions, acceleration near impact, or biological processes.
Yes. A function may oscillate, curve sharply, or vary unevenly near a point, yet still have a well-defined instantaneous rate there.
What matters is whether the slope of the secant lines approaches a single value as the interval shrinks. If they do, the derivative exists regardless of nearby irregularities.
Not always. A zero derivative indicates no change at that instant, but it does not guarantee a local extremum.
Flat points on inflection curves and points in piecewise contexts can also produce a zero derivative without representing maxima or minima.
Units ensure that the rate aligns with the quantities being described. Checking them can quickly reveal interpretation errors.
For example:
• If a function measures pressure over time, the derivative should have units of pressure per unit time.
• Mismatched or nonsensical units indicate a misunderstanding of what is changing with respect to what.
Practice Questions
A function g models the depth of water in a tank, measured in metres, t minutes after filling begins. At t = 4, the derivative g'(4) = 0.6.
• 1 mark for stating that at t = 4 minutes the depth of water is increasing.
• 1 mark for stating that it is increasing at a rate of 0.6 metres per minute.
The temperature of a metal rod, measured in degrees Celsius, is given by T(x), where x is the distance in centimetres from one end of the rod. The derivative T'(x) represents the instantaneous rate of change of temperature with respect to distance.
(a) Explain what T'(5) = -3 means in context.
(b) The average rate of change of temperature between x = 5 and x = 9 is -2.1 degrees Celsius per centimetre. Explain how the instantaneous rate of change at x = 5 differs from this average rate.
(c) Discuss what the sign of T'(x) tells you about how the temperature varies along the rod.
(a)
• 1 mark for stating that at x = 5 cm the temperature is decreasing.
• 1 mark for stating that it is decreasing at a rate of 3 degrees Celsius per centimetre at that exact point.
(b)
• 1 mark for correctly identifying that the average rate of change summarises the change over the whole interval 5 to 9 cm.
• 1 mark for explaining that the instantaneous rate of change describes the rate at exactly x = 5 cm, not over a range.
(c)
• 1 mark for stating that a negative derivative indicates temperature decreases as x increases.
• 1 mark for stating that a positive derivative would indicate temperature increasing along the rod.

