This section explains how L’Hospital’s Rule allows indeterminate limits of ratios to be evaluated by differentiating numerator and denominator, offering a powerful method for resolving otherwise inaccessible limits.

Understanding the Purpose of L’Hospital’s Rule

L’Hospital’s Rule is used only when a limit of a ratio results in an indeterminate form, meaning that the expression does not immediately reveal its limiting behavior. The rule provides a structured way to transform such limits into forms that are simpler to evaluate. Before applying the rule, students must fully understand what qualifies as an indeterminate form and why direct substitution may fail.

When discussing indeterminate forms, we typically encounter situations where substituting a value into a ratio yields 0/0 or ∞/∞. Because both of these expressions lack meaningful numerical interpretation, a new strategy is required to uncover the limit’s true value.

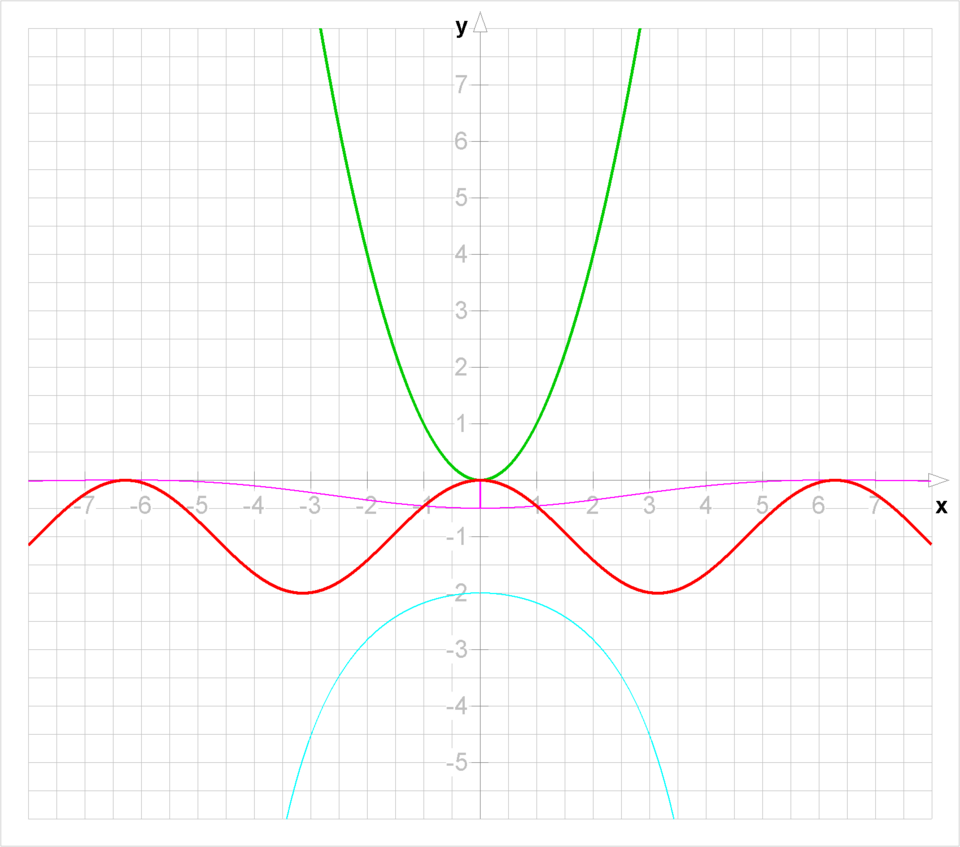
This graph displays curves based on $\cos(x)-1$ and $x^2$ together with quotient functions that reveal how ratios behave when both numerator and denominator approach zero. Near the origin, it illustrates how the quotient can settle toward a well-defined limit despite yielding the indeterminate form $0/0$ under direct substitution. The reciprocal quotient included exceeds AP requirements but helps highlight contrasting limit behavior. Source.

Indeterminate Form

The presence of an indeterminate form signals that further analysis is needed, and L’Hospital’s Rule becomes an appropriate tool when its conditions are satisfied.

Conditions for Using L’Hospital’s Rule

Before applying the rule, students must check several requirements to ensure mathematical validity. These checks guarantee that the transformation of the limit is legitimate and that differentiation will not create new issues with domain or behavior.

To use L’Hospital’s Rule correctly, the following must be true:

• The limit produces 0/0 or ∞/∞ when substituted.

• Both the numerator and denominator are differentiable near the point of interest.

• The derivative of the denominator is not zero in a neighborhood around the point.

• The limit of the ratio of derivatives exists or approaches ±∞.

Only after verifying these conditions can a student proceed confidently.

A ratio of derivatives often provides clearer insight into the limiting value because differentiation typically simplifies functions or exposes structural behavior that was not obvious in the original ratio.

The Statement of L’Hospital’s Rule

When L’Hospital’s Rule applies, students may replace the original limit of a ratio with the limit of the ratio of their derivatives. This substitution is not algebraic manipulation but a theoretical result grounded in calculus concepts of differentiability and function behavior.

This formulation emphasizes that the original limit and the transformed limit are equal only under the required conditions.

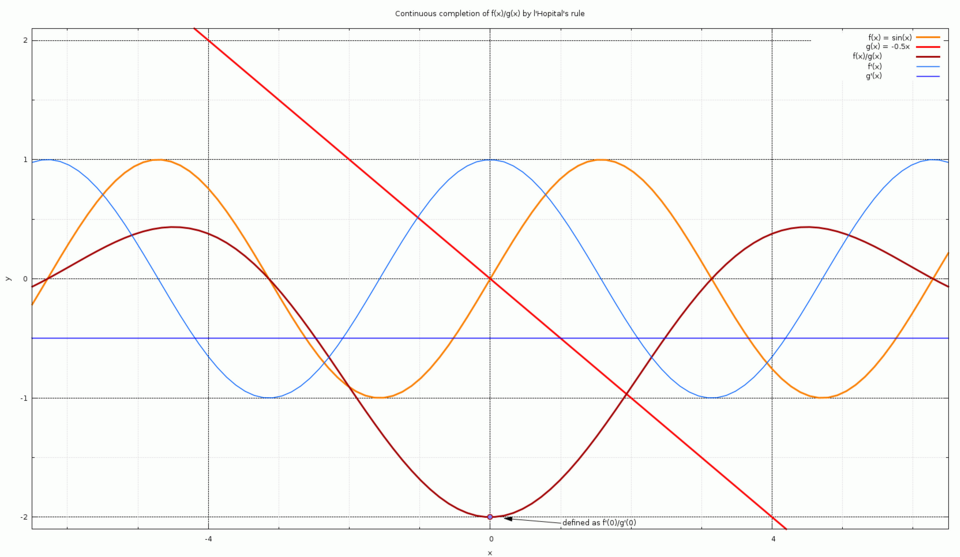
This plot depicts $f(x)=\sin x$, $g(x)=-0.5x$, and their quotient alongside the constant value produced by applying L’Hospital’s Rule at $x=0$. The highlighted point shows how defining the quotient using $f'(0)/g'(0)$ repairs the discontinuity caused by the indeterminate form. The additional derivative curves exceed AP expectations but serve to clarify how the rule anchors the limit in local behavior. Source.

The appearance of derivatives in L’Hospital’s Rule reflects how limits often depend on the local behavior of functions, and derivatives precisely measure this behavior. This method aligns with the AP Calculus AB emphasis on understanding how functional changes near a point influence limiting values.

Applying L’Hospital’s Rule Thoughtfully

Using the rule involves more than blindly differentiating. Students must think critically about whether repeated applications are necessary, whether the transformed limit is still indeterminate, and whether alternative limit strategies might be more appropriate.

When applying L’Hospital’s Rule:

• Confirm the original limit is indeterminate.

• Differentiate numerator and denominator separately.

• Reevaluate the resulting limit.

• Repeat the rule only if new indeterminate forms arise.

• Stop once the limit can be computed directly or evaluated using known limit techniques.

Sometimes the derivative ratio simplifies dramatically, revealing the limit immediately. Other times, further algebraic manipulation or a second application of the rule is required. Students must resist the temptation to apply the rule prematurely, as doing so could lead to incorrect conclusions.

Interpreting the Result of L’Hospital’s Rule

The limit found using the ratio of derivatives describes the behavior of the original functions near the point of interest. In other words, the rule does not replace the meaning of the original limit; rather, it provides an alternate path to finding that meaning.

The resulting limit conveys:

• How the numerator and denominator grow relative to each other.

• Whether the ratio stabilizes, diverges, or approaches zero.

• The underlying behavior of the original functions near the limit point.

Understanding this relationship is essential in AP Calculus AB, where interpreting results is just as important as computing them. L’Hospital’s Rule thus serves as both a computational tool and a conceptual lens for examining limiting behavior.