AP Syllabus focus:
‘When these conditions hold, the Mean Value Theorem guarantees at least one point c in (a,b) where the instantaneous rate of change equals the average rate of change.’
The Mean Value Theorem ensures that under appropriate conditions, a function’s instantaneous rate of change must match its average rate somewhere, creating a powerful bridge between algebraic and geometric reasoning.
Understanding the Guaranteed Point
The Mean Value Theorem (MVT) states that if a function is continuous on a closed interval and differentiable on the corresponding open interval, then a special point exists where the instantaneous rate of change equals the average rate of change. This subsubtopic focuses specifically on the theorem’s guarantee of such a point and the conceptual meaning of that equality.
### The Instantaneous and Average Rates of Change
To appreciate what the MVT guarantees, it is essential to distinguish two key ideas: the instantaneous rate of change and the average rate of change.
Instantaneous Rate of Change: The derivative , representing the slope of the tangent line to a function at a single point.
A sentence separates definition blocks to maintain clarity before introducing the next idea.
Average Rate of Change: The slope of the secant line across an interval, computed as .
These two types of rate describe different perspectives on how a function behaves. The instantaneous rate captures behavior at a precise moment, while the average rate captures behavior over an entire interval.
The MVT Guarantee
Once the continuity and differentiability conditions of the MVT are met, the theorem ensures the existence of a point c strictly inside the interval such that the two rates of change match.
The significance of this equality is more than symbolic. It establishes that somewhere between the endpoints of the interval, the function behaves moment-by-moment exactly as it behaves on average over the entire stretch.
A normal sentence is placed here to maintain the required separation before another equation.
= A value in the open interval where the tangent slope equals the secant slope
This relationship captures the heart of the MVT: even if a function appears irregular or uneven across an interval, the theorem guarantees a moment of perfect alignment between local and global behavior.
Geometric Meaning of the Guaranteed Point
The MVT’s guarantee becomes especially intuitive when viewed geometrically. The slope of the secant line through and gives the overall direction and steepness of the function across the entire interval. Geometrically, this means there is at least one point c in (a,b) where the slope of the tangent line equals the slope of the secant line across the interval.
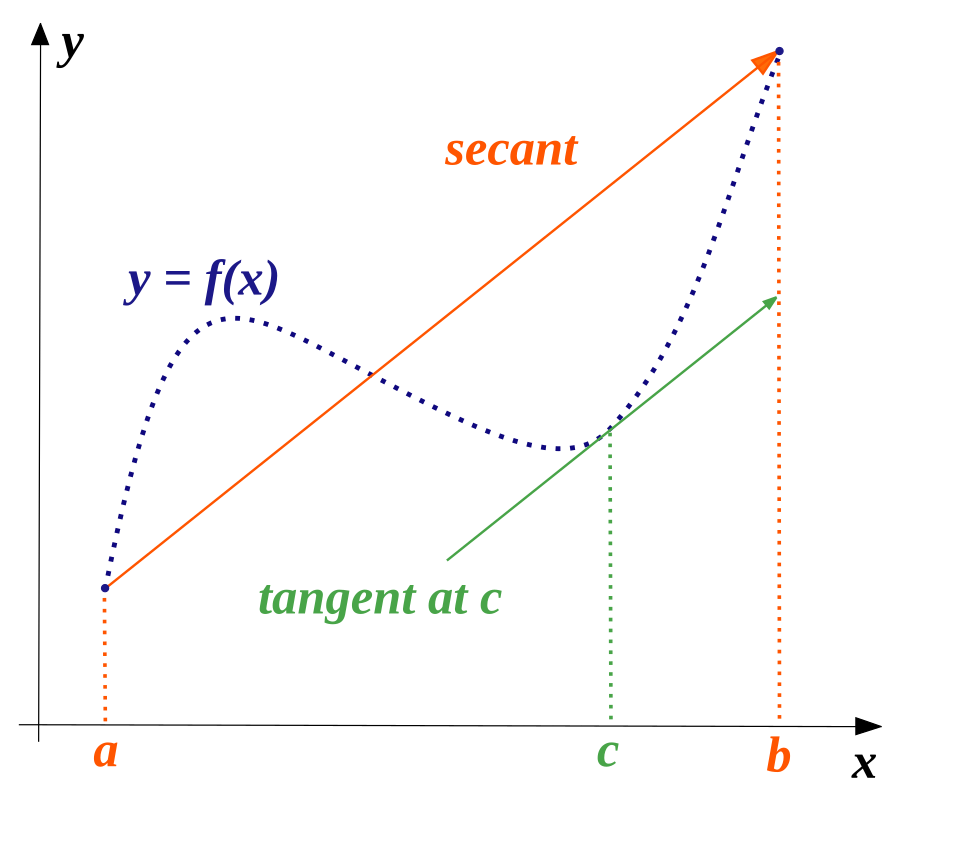
A smooth curve is shown with endpoints \((a,f(a))\) and \((b,f(b))\) joined by a secant line representing the average rate of change on \([a,b]\). At an interior point \(c\), the tangent line has the same slope as the secant line, illustrating . This picture emphasizes the Mean Value Theorem’s guarantee that at least one point has instantaneous rate of change equal to the average rate of change. Source.
Why This Matching Point Must Exist
The guaranteed point exists because continuity ensures the function has no jumps or gaps, and differentiability ensures smoothness within the interval. Together, these conditions prevent abrupt shifts that would make matching slopes impossible. The result is a predictable structure in which the function’s local behavior must reflect its overall change.
Key Observations
The guarantee provided by the MVT is often summarized through several reliable observations:
- The point c is always located inside, never at the endpoints of the interval.
- The tangent line at c is parallel to the secant line across .
- The theorem ensures at least one matching point, but there may be many.
- The guarantee applies only when continuity and differentiability conditions are fully satisfied.
Interpreting the Matching of Rates
Understanding what it means for the instantaneous and average rates of change to match deepens a student’s conceptual grasp of the theorem. When the tangent line’s slope equals the secant line’s slope, the behavior of the function at that specific moment mirrors its behavior across the entire interval. This reveals an inherent structure in differentiable functions: they cannot average a certain rate of change without achieving that rate somewhere in between.
In other words, there is at least one point c in (a,b) where the instantaneous rate of change f′(c) equals the average rate of change \(\dfrac{f(b)-f(a)}{b-a}\).
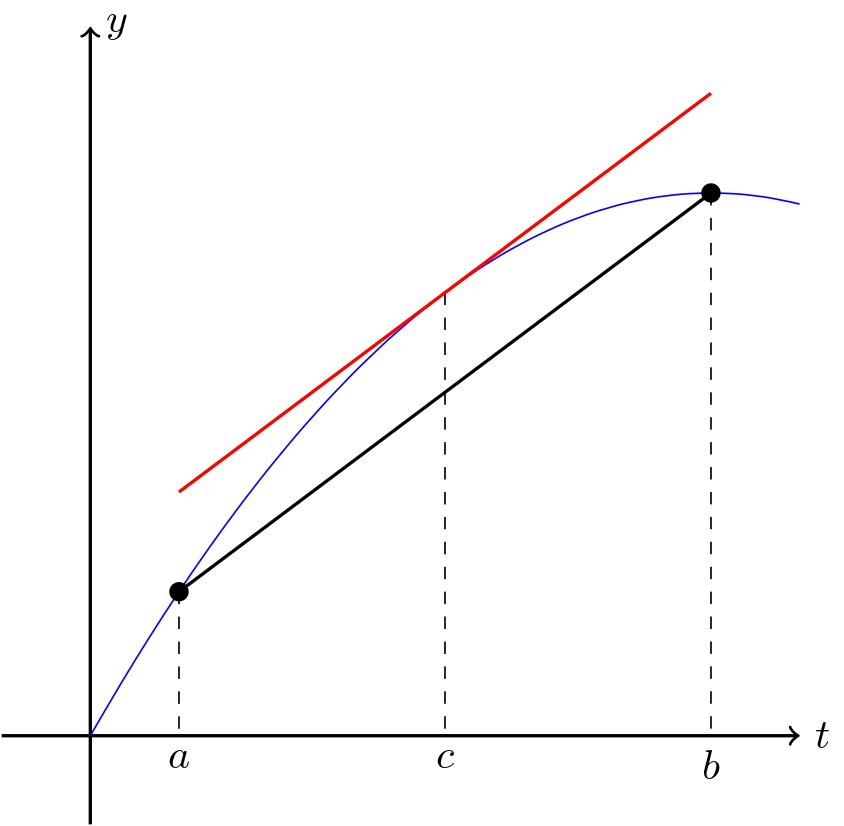
The blue curve represents a function \(y=f(t)\) that is continuous on \([a,b]\) and differentiable on \((a,b)\). A black secant line connects \((a,f(a))\) and \((b,f(b))\), while a red tangent line at an interior point \(c\) has the same slope as this secant line, illustrating . This graph directly visualizes the Mean Value Theorem’s guarantee of at least one point where instantaneous and average rates of change match. Source.
Why the Guarantee Matters
The existence of this matching point has broad implications across calculus. It serves as a foundation for many later results, including understanding motion, establishing inequalities, and proving relationships between functions. The MVT’s guarantee ensures that when a function changes by a certain amount over an interval, it must exhibit consistent behavior somewhere within that interval. This principle helps explain natural phenomena such as why a moving object with an average speed must at some moment match that speed exactly, though the details of such applications extend beyond the focus of this subsubtopic.
FAQ
The Mean Value Theorem does not require the function to increase smoothly; it only requires continuity and differentiability. Even if the function has long stretches of slow growth and short bursts of rapid change, a point c must still exist where the instantaneous rate matches the average rate.
In highly uneven functions, c may be located in a region where the function transitions between different rates of change, but the theorem guarantees at least one such point regardless of how irregular the growth is.
Yes. The theorem only guarantees at least one such point, but many functions contain several.
This occurs frequently when the graph fluctuates around the secant slope. Each time the tangent line’s slope equals the secant slope, another valid c arises, and the Mean Value Theorem makes no restriction on how many may exist.
Indirectly. The secant slope sets the value that the derivative must match. If the secant slope is large, c must lie in a region where the function rises quickly.
• A steep secant slope forces c to occur where the tangent matches that steepness.
• A flatter secant slope allows c to occur in regions of gentler growth.
The interval endpoints do not necessarily affect where c appears beyond defining the secant.
Endpoints cannot serve as candidates because the derivative is defined using limits from both sides, and at an endpoint only a one-sided limit exists.
The Mean Value Theorem requires differentiability at interior points so that the tangent line is fully defined. Consequently, even if the derivative at an endpoint equals the average rate of change, it cannot be used as the guaranteed c.
The curvature and local behaviour of the graph guide where the tangent slope is able to match the secant slope.
• Regions where the function bends steeply may produce tangents that overshoot or undershoot the secant slope.
• Regions where the graph changes slope gradually often contain points where the derivative equals the secant slope.
Thus, while the theorem ensures a c exists, the graph’s geometry determines where it is found.
Practice Questions
Question 1 (1–3 marks)
A function g is continuous on the closed interval [2, 7] and differentiable on the open interval (2, 7). The values of g(2) and g(7) are 5 and 18 respectively.
Explain why there must be at least one number c in (2, 7) such that g′(c) = 13/5.
Question 1 (1–3 marks)
• 1 mark: States or implies that the function satisfies the conditions of the Mean Value Theorem (continuous on [2, 7] and differentiable on (2, 7)).
• 1 mark: Identifies the average rate of change as (18 − 5) / (7 − 2) = 13/5.
• 1 mark: Concludes that by the Mean Value Theorem there exists a c in (2, 7) such that g′(c) equals this average rate of change.
Question 2 (4–6 marks)
A function h is continuous on the interval [0, 6] and differentiable on (0, 6). It is known that h(0) = 4 and h(6) = 10.
(a) State the Mean Value Theorem and the conditions needed for it to apply.
(b) Show that there must be at least one value c in (0, 6) for which h′(c) = 1.
(c) Briefly describe the geometric meaning of the conclusion in part (b).
Question 2 (4–6 marks)
• Part (a) – 2 marks:
– 1 mark: States that if a function is continuous on a closed interval and differentiable on the corresponding open interval,
– 1 mark: then there exists at least one c in the open interval where the derivative equals the average rate of change.
• Part (b) – 2 marks:
– 1 mark: Computes the average rate of change: (10 − 4) / 6 = 1.
– 1 mark: States that by the Mean Value Theorem there is a c in (0, 6) such that h′(c) equals this value.
• Part (c) – 1–2 marks:
– 1 mark: Describes that the tangent line at x = c is parallel to the secant line joining (0, 4) and (6, 10).
– 1 additional mark (optional for full clarity): Explains that this means the instantaneous rate of change matches the overall average rate of change on the interval.

