AP Syllabus focus:
“For the Mean Value Theorem to apply, a function must be continuous on the closed interval [a,b] and differentiable on the open interval (a,b).”
The Mean Value Theorem relies on specific structural requirements for a function. Understanding these conditions ensures correct application and prevents misinterpretation of one of calculus’s most foundational results.
Understanding the Conditions of the Mean Value Theorem
To use the Mean Value Theorem (MVT) effectively, students must understand the strict requirements that guarantee its validity. The theorem does not apply to every function on every interval, and its conclusions hold only when the appropriate hypotheses are satisfied. These hypotheses ensure that the function behaves smoothly enough on the chosen interval so that a point exists where the instantaneous rate of change aligns with the average rate of change.
The Setting: Closed and Open Intervals
The MVT specifically requires examining the behavior of a function on two connected intervals: the closed interval and the open interval . These intervals are related but serve distinct conceptual purposes:
The closed interval includes the endpoints and is used for assessing overall behavior of the function.
The open interval excludes endpoints and is used for evaluating derivative behavior, which must not include abrupt changes or undefined slopes at endpoints.
This structure mirrors many real-world settings in which a function must meet overall constraints while also varying smoothly in its interior.
These hypotheses describe a function that is unbroken on [a,b][a,b][a,b] and smooth on (a,b)(a,b)(a,b), providing the precise setting in which the Mean Value Theorem can be applied.
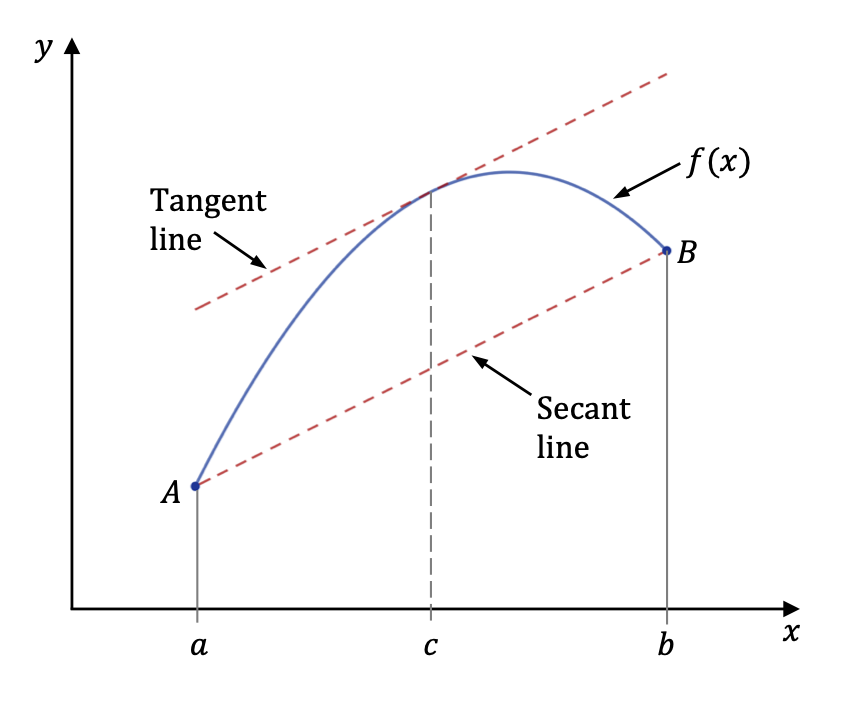
A smooth curve y=f(x)y=f(x)y=f(x) spans the interval [a,b][a,b][a,b] with a secant line connecting its endpoints, and at an interior point ccc, a tangent line parallels the secant. This illustrates the Mean Value Theorem when continuity and differentiability conditions are satisfied. The diagram emphasizes the point where the instantaneous slope equals the average slope across the interval. Source.
Condition 1: Continuity on the Closed Interval
The first essential condition states that the function must be continuous on the entire closed interval . When continuity is first introduced in the notes, it must be defined for clarity.
Continuity: A function is continuous at a point if its value at that point equals the limit of the function as the input approaches that same point.
Informally, a continuous function on [a,b][a,b][a,b] is one whose graph can be drawn from x=ax=ax=a to x=bx=bx=b without lifting your pencil.
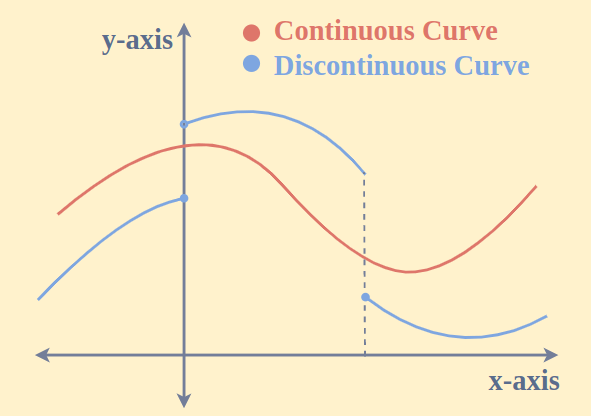
A red curve moves smoothly across the interval with no gaps, while the blue curve contains a visible jump illustrating a discontinuity. This highlights that the continuity requirement prohibits breaks, holes, or jumps anywhere on [a,b][a,b][a,b]. The visual contains general continuity information consistent with the concept emphasized here.
Continuity ensures there are no breaks, gaps, or jumps anywhere in the interval, including at the endpoints. This requirement is crucial because the MVT compares overall function behavior at and . If a discontinuity existed anywhere on , the average rate of change might not reflect any true behavior inside the interval.
Why Continuity Matters
If a function were not continuous on :
The connection between the endpoints could be disrupted.
The average rate of change might not correspond to any real slope in the interior.
The smoothness needed to guarantee a matching instantaneous rate of change could be lost.
Therefore, continuity serves as the foundation for applying the theorem.
Condition 2: Differentiability on the Open Interval
The second requirement states that a function must be differentiable on the open interval , meaning it must have a well-defined derivative at every point strictly between and .
Differentiability: A function is differentiable at a point if it has a defined derivative there, meaning it has a unique tangent line and no sharp corners or cusps.
A function can be continuous on the whole interval but still fail to be differentiable at an interior point because of a sharp corner, cusp, or vertical tangent.
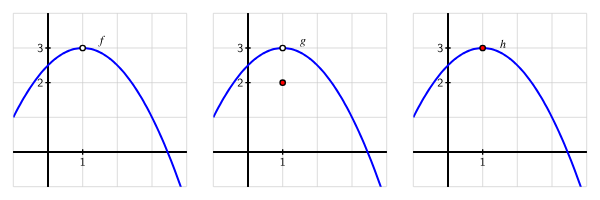
The left graph shows a continuous function that forms a sharp V-shaped corner at x=1x=1x=1, while the right graph zooms in to highlight the nondifferentiable point. This demonstrates that continuity alone does not guarantee differentiability. The figure includes a specific corner example, reinforcing that such a point breaks the differentiability requirement for the Mean Value Theorem. Source.
Differentiability inherently implies continuity on the same interval, but only for interior points. Because the function must also be continuous at endpoints, the continuity requirement on must still be stated explicitly.
Why Differentiability Matters
Differentiability guarantees:
The instantaneous rate of change exists everywhere inside the interval.
The graph has no abrupt turns or vertical tangents within .
The function behaves smoothly enough that one can search for a point where its instantaneous slope equals the average slope.
Without differentiability, the derivative may fail to exist, preventing the MVT’s conclusion from being valid.
Understanding the Relationship Between the Two Conditions
Even though continuity and differentiability are separate conditions, they work together to create the environment in which the MVT applies. Continuity ensures the function’s outputs connect smoothly; differentiability ensures that the rates of change inside the interval are meaningful and well-defined.
A useful way to visualize the relationship is to consider the following layered structure:
Continuity on ensures the function links the endpoints without interruption.
Differentiability on ensures there is no interior point where the slope becomes undefined or unreasonable.
Together, these conditions guarantee the existence of at least one point where the derivative matches the average rate of change.
Situations Where Conditions Fail
The MVT cannot be applied in circumstances such as:
A jump discontinuity anywhere in
A removable discontinuity at an interior or endpoint
A cusp or corner anywhere in
A vertical tangent on
A derivative that becomes undefined on any interior point
Each failure blocks one of the theorem’s required hypotheses, making its conclusion invalid.
Summary of Key Requirements
To apply the Mean Value Theorem correctly, students should verify the following checklist:
Continuity on
No breaks, jumps, or holes anywhere on the interval
Function is defined at every point, including endpoints
Differentiability on
Derivative exists at all interior points
No corners, cusps, or vertical tangents
Both conditions must be satisfied before the theorem’s conclusion can be invoked.
FAQ
A closed interval ensures the function has defined values at both endpoints so that an average rate of change can be computed. Without these endpoint values, the secant slope that the theorem relies on would not be well defined.
An open interval would prevent evaluation at the edges, making it impossible to relate endpoint behaviour to a point inside the interval.
Yes. A function may fail to be continuous at an endpoint yet still have a derivative at every interior point. In such a case, the function satisfies differentiability where required but fails the continuity condition on the closed interval.
This means the Mean Value Theorem would not apply, as the endpoint continuity requirement is essential.
Look for visual features that break differentiability, such as:
• Sharp corners
• Cusps
• Vertical tangents
• Sudden changes in slope direction
If any of these appear at an interior point, the function is not differentiable on the interval.
Yes, but only if the filling makes the function truly continuous on the closed interval. A removable discontinuity does not violate the theorem once it has been corrected.
The function must also be differentiable at all interior points; continuity alone is not enough.
The derivative describes instantaneous change, which is only meaningful where the function has neighbouring points on both sides. Endpoints lack this two-sided structure, so differentiability is not defined there.
The theorem therefore avoids requiring differentiability at the endpoints and restricts the condition to the open interval.
Practice Questions
Question 1 (1–3 marks)
A function g is continuous on the closed interval [2, 7] but has a sharp corner at x = 5.
State whether the Mean Value Theorem can be applied to g on [2, 7], giving a reason for your answer.
Mark scheme:
• 1 mark: States correctly that the Mean Value Theorem cannot be applied.
• 1 mark: Gives the correct reason that g is not differentiable at x = 5.
• 1 mark: Notes that differentiability on the entire open interval (2, 7) is required for the theorem.
Question 2 (4–6 marks)
Let f be a function that is continuous on [−3, 4] and differentiable on (−3, 4). The values f(−3) = 2 and f(4) = 12 are known.
(a) Explain why the Mean Value Theorem applies to f on [−3, 4].
(b) State what the theorem guarantees about the existence of a number c in the interval (−3, 4).
(c) Calculate the average rate of change of f on [−3, 4].
(d) State the relationship between f′(c) and the value found in part (c).
Mark scheme:
• (a) 1 mark: States that f is continuous on the closed interval and differentiable on the open interval.
• (a) 1 mark: Concludes correctly that the Mean Value Theorem therefore applies.
• (b) 1 mark: States that there exists a number c in (−3, 4) where the instantaneous rate of change equals the average rate of change.
• (c) 1 mark: Calculates (12 − 2) / (4 − (−3)) = 10 / 7.
• (d) 1 mark: States that f′(c) equals 10 / 7.
• (d) 1 mark: Correctly identifies that this equality is the conclusion guaranteed by the Mean Value Theorem.

