AP Syllabus focus:
‘The Extreme Value Theorem says that if a function is continuous on a closed interval [a,b], then it has at least one absolute minimum and one absolute maximum on that interval.’
A central idea in calculus is understanding when a function is guaranteed to achieve its highest and lowest values on a specific interval, which is precisely what the Extreme Value Theorem explains.
Understanding the Extreme Value Theorem
The Extreme Value Theorem (EVT) is one of the foundational results in differential calculus because it ensures the existence of extreme values under specific conditions. The theorem applies only when a function satisfies two essential properties: it must be continuous and defined on a closed interval. These conditions make the behavior of the function stable enough for its highest and lowest values to be guaranteed within the interval.
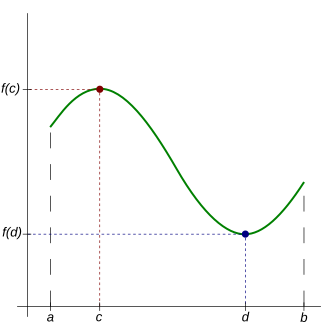
A continuous function f(x)f(x)f(x) on the closed interval [a,b][a,b][a,b] with absolute maximum and minimum marked. This illustrates that when the EVT conditions are satisfied, the function truly attains its extreme values. The diagram emphasizes that EVT guarantees achieved, not merely approached, extrema. Source.
When we say a function is continuous, we mean there are no breaks, jumps, or holes in the graph. Continuity ensures predictable behavior and allows values at endpoints and interior points to be compared meaningfully.
Continuity on an Interval: A function is continuous on an interval if its graph has no breaks, jumps, or holes at any point within that interval.
The idea of a closed interval, written as [a, b], means that both endpoints a and b are included in the interval. This is crucial for EVT because the absolute maximum or minimum can occur at the endpoints, and excluding them could prevent the function from achieving extreme values there.
Why the Conditions Matter
The conditions in EVT are not optional; they are necessary for the theorem’s guarantee to hold. Understanding why these requirements are essential helps reinforce the intuition behind the theorem.
Continuity Requirement
If a function is not continuous on the interval, it may “jump over” its maximum or minimum values. A discontinuity could create a situation where the function approaches an extreme value without ever reaching it, making the extreme value nonexistent.
A continuous function avoids these complications by ensuring that all intermediate values between any two points in the interval are attained, meaning there are no missing function outputs.
Closed Interval Requirement
The insistence on a closed interval matters because the endpoints themselves may be where the extreme values occur. If an interval is open, written as (a, b), the function is not defined at the endpoints, and it may get arbitrarily close to extreme values without ever achieving them.
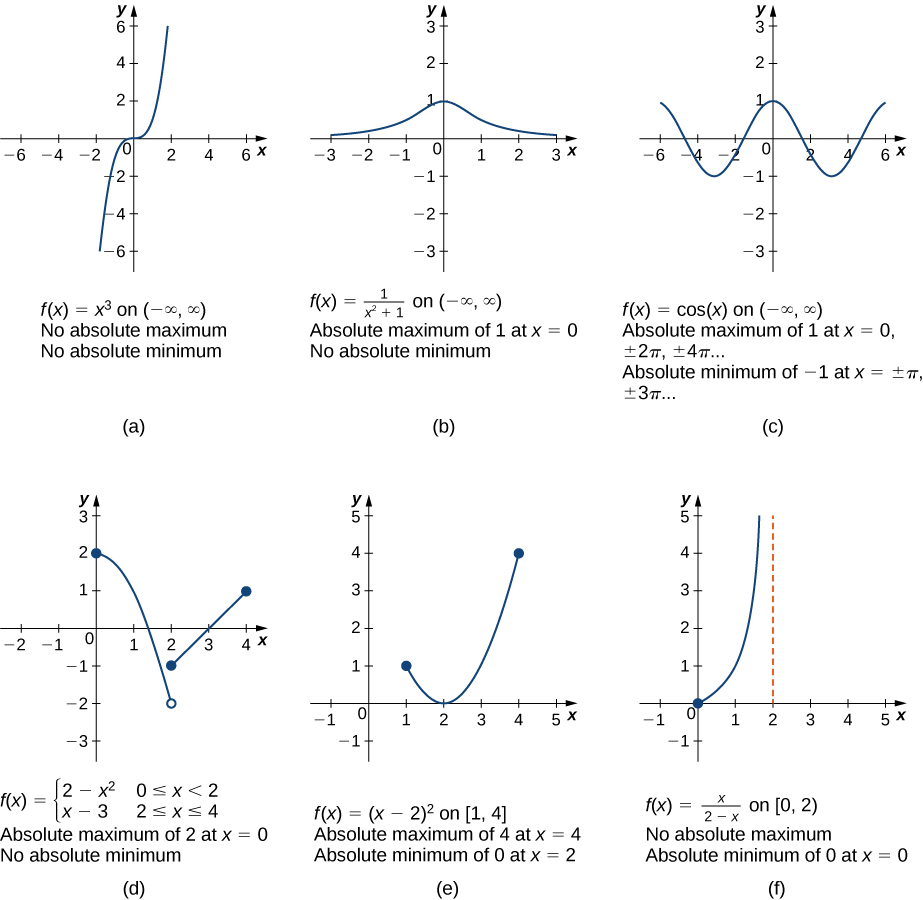
A comparison of several graphs illustrating when absolute extrema may or may not exist. Panels highlight how discontinuities or missing endpoints can prevent extrema even on bounded intervals. Some panels include whole-real-line examples, which exceed the subtopic slightly but still clarify why EVT conditions are required. Source.
Because EVT guarantees the existence of actual values—not just limits—it requires access to the endpoints, ensuring that comparisons include every point where an extreme value might occur.
Absolute Maximum and Minimum
The EVT guarantees the existence of absolute extrema, which are function values that are the highest or lowest on the entire interval. These extremum values may occur at interior points or at the endpoints.
Absolute Maximum: The greatest function value achieved on the interval.
Absolute Minimum: The least function value achieved on the interval.
Because the theorem does not indicate how to find the extrema, it is important to distinguish EVT from methods of locating extreme values. EVT only confirms that extrema exist; locating them requires additional tools such as derivatives or direct evaluation.
Interpreting the Guaranteed Extremes
The EVT applies broadly across continuous functions, making it a powerful conceptual tool. When a function meets its conditions, we can rely on the theorem to assert the following:
The function reaches at least one highest point on the interval.
The function reaches at least one lowest point on the interval.
These extreme values are actual outputs of the function, not merely approached values.
The extreme values can occur either at endpoints or at interior points.
This assurance is especially useful in mathematical modeling, where extreme values often correspond to maximum profit, minimum cost, highest speed, or lowest temperature.
Visual and Conceptual Understanding
One helpful way to think about the EVT is to imagine drawing the graph of a continuous function on a closed interval without lifting your pencil. Since the interval includes both endpoints, the graph begins at a definite point and ends at another definite point. Because the function is continuous between these points, the graph fills the entire region without gaps. A complete, uninterrupted graph over a closed interval must reach some highest and lowest vertical positions, ensuring the existence of absolute maxima and minima.
This visualization reinforces that the EVT describes the inherent stability in continuous behavior. A continuous function over a closed interval cannot avoid reaching extremes because its graph cannot escape the vertical bounds created by its domain restrictions and continuity.
Key Takeaways for AP Calculus Students
EVT guarantees the existence of absolute extrema only when the function is continuous on a closed interval.
The theorem does not help identify where the extrema occur; it only ensures they exist.
Both endpoints and interior points are valid locations for absolute extrema.
Continuity prevents “gaps,” while a closed interval ensures the endpoints are available as candidates for extreme values.
FAQ
No. The theorem guarantees existence, not uniqueness. A function may have more than one x-value where it attains its absolute maximum or absolute minimum.
This can occur when the function takes the same highest or lowest value at multiple points, such as in flat regions or repeated peaks.
Yes, provided the piecewise function is continuous on the entire closed interval. Each transition point must match in value from both sides to avoid a discontinuity.
To verify continuity in such cases:
• Check that each piece is continuous on its own domain.
• Ensure the pieces join with matching values at their boundaries.
The two theorems guarantee different things. The Intermediate Value Theorem ensures that all intermediate outputs are attained, while the Extreme Value Theorem ensures that the highest and lowest outputs are attained.
Although both require continuity, only the Extreme Value Theorem requires a closed interval, because endpoints play a role in determining extremes.
No. If a function meets the EVT conditions, it must have both an absolute maximum and an absolute minimum. If either extremum does not exist, then at least one of the conditions of the theorem must have failed.
Typical causes include:
• The interval is open.
• The function is not continuous at one or more points.
• The domain is unbounded.
Closed intervals are automatically bounded, and boundedness ensures that the function cannot extend indefinitely without reaching extreme values.
If an interval were closed but unbounded, the function could grow without limit, making an absolute maximum impossible. The requirement of a closed and bounded interval prevents this issue and ensures extremes are attainable.
Practice Questions
Question 1 (1–3 marks)
A function g is continuous on the closed interval [2, 7]. Explain what the Extreme Value Theorem guarantees about g on this interval.
Question 1
• 1 mark: States that the function must have an absolute maximum on the interval.
• 1 mark: States that the function must have an absolute minimum on the interval.
• 1 mark: Makes clear that the guarantee comes from continuity on a closed interval.
Question 2 (4–6 marks)
Let h be a function that is continuous on the interval [−3, 5].
(a) State the conditions under which the Extreme Value Theorem applies.
(b) Explain why these conditions ensure that h must attain both an absolute maximum and an absolute minimum on [−3, 5].
(c) Give one reason why the conclusion of the theorem may fail if the interval is not closed.
Question 2
(a)
• 1 mark: States that the function must be continuous.
• 1 mark: States that the interval must be closed (and bounded).
(b)
• 1 mark: Explains that continuity prevents jumps or gaps, ensuring all intermediate values are taken.
• 1 mark: Explains that including the endpoints means extreme values can occur there as well as in the interior.
• 1 mark: Concludes that therefore both an absolute maximum and an absolute minimum must exist.
(c)
• 1 mark: Correctly identifies that if the interval is not closed, an extreme value may occur at an endpoint that is not included, meaning the function may approach but never attain the extremum.

