AP Syllabus focus:
‘Given an integrand expressed as a product, choose functions u and dv strategically so integration by parts simplifies the remaining integral.’
Integration by parts becomes far more effective when the original integrand is reorganized so that one part differentiates cleanly and the other integrates without complication, making strategic choices essential.
Understanding the Purpose of Choosing u and dv
Integration by parts is based on rewriting an integral of a product into a more manageable form. The selection of u and dv determines whether the resulting integral becomes simpler or more difficult. A thoughtful choice reduces complexity and supports efficient computation, which aligns directly with the syllabus requirement to choose components so the remaining integral is easier to evaluate.
The Integration by Parts Identity
Before selecting u and dv, recall the structure of the method.
This diagram shows the integration by parts identity , highlighting the roles of , , , and . It emphasizes that once is differentiated to and is integrated to , the original integral is transformed into a new, hopefully simpler integral. The image contains only the formula and labels, with no additional content beyond the syllabus requirements. Source.
= Function chosen for differentiation
= Function chosen for integration
= Antiderivative of
= Derivative of
Understanding how each component transforms helps guide the strategy for choosing them effectively.
Criteria for Selecting u
A productive choice of u leads to a derivative that is simpler than the original function. This simplification reduces the difficulty of the subsequent integral and prevents unnecessary algebraic expansion.
Common Indicators That a Term Should Be u
The term becomes simpler when differentiated, often losing powers or converting to a manageable trigonometric or logarithmic form.
The term forms a meaningful derivative that pairs well with the integrated form of dv.
The term is difficult to integrate, which is a strong sign it should not be chosen as dv.
Useful Heuristics for Choosing u
The well-known LIATE hierarchy provides a helpful but flexible guide. It suggests choosing u from highest priority to lowest:
Logarithmic functions
Inverse trigonometric functions
Algebraic expressions (polynomials)
Trigonometric functions
Exponential functions
This list reflects how easily each type differentiates compared to how they integrate.
Criteria for Selecting dv
Once a suitable u is chosen, the remaining part of the integrand becomes dv. Because the method requires integrating dv to obtain v, the choice must ensure that this integration step is doable with known antiderivative rules.
Features of a Good dv
It is easy to integrate using familiar formulas.
It complements u so that the resulting product uv does not introduce complexity greater than the original integrand.
It does not produce a result for v that complicates the new integral more than necessary.
When dv Should Not Be Chosen
Avoid choosing dv from components that:
Create antiderivatives involving inverse trigonometric or other complicated expressions without benefit.
Have no elementary antiderivative, which would prevent completion of the process.
Produce a v that interacts poorly with du, leading to an integral more complex than the starting point.
A careful decision prevents the integration by parts process from cycling without progress.
Balancing Simplicity Between du and v
Even when a term seems to be a strong candidate for u or dv, the key question remains whether the result of substituting both choices into the formula simplifies the remaining integral. Because integration by parts transforms the original integral into a new integral, the quality of this new expression determines success.
Strategic Considerations
After differentiating u, the resulting du should reduce in algebraic complexity.
The antiderivative v should remain manageable, avoiding expressions that inflate the complexity of .
The product uv should be simpler to evaluate at boundaries when integration by parts is applied to definite integrals.
Even small adjustments to which function is labeled u or dv can significantly affect the difficulty of integration.
Using Structure to Guide the Choice
Recognizing patterns in integrands strengthens decision-making. Many functions appear frequently in AP Calculus AB problems, and the structural clues they present can guide the decomposition.
Structural Clues
Polynomial × exponential: The polynomial typically becomes u because it reduces upon differentiation.
Polynomial × trigonometric: Again, the polynomial often serves as u, while the trigonometric function becomes dv.
Logarithmic × anything: The logarithmic function almost always becomes u because it simplifies drastically when differentiated.
Inverse trigonometric × algebraic: The inverse trigonometric function generally becomes u by the same reasoning.
This structure-driven approach aligns with common patterns students encounter on the AP exam.
Avoiding Common Pitfalls in Choosing u and dv
Common errors arise when the selection ignores the long-term consequences of the choices.
Frequent Missteps
Choosing dv to be a part of the integrand that yields a more complicated antiderivative than the original expression.
Selecting u that becomes more complex when differentiated, making du harder to manage.
Ignoring whether the new integral is truly simpler, which is essential to the method’s success.
Careful attention to how each transformation affects the resulting expressions ensures that integration by parts remains a tool for simplification rather than complication.
Developing Flexibility in Strategy
Although heuristics are helpful, they are not absolute rules. Skilled students adapt their choices to match the specific structure of the integrand. In some cases, trying one arrangement may reveal that the resulting integral becomes unwieldy, indicating that reversing the roles of u and dv is more appropriate. Thinking strategically while adhering to the syllabus focus leads to stronger problem-solving habits.
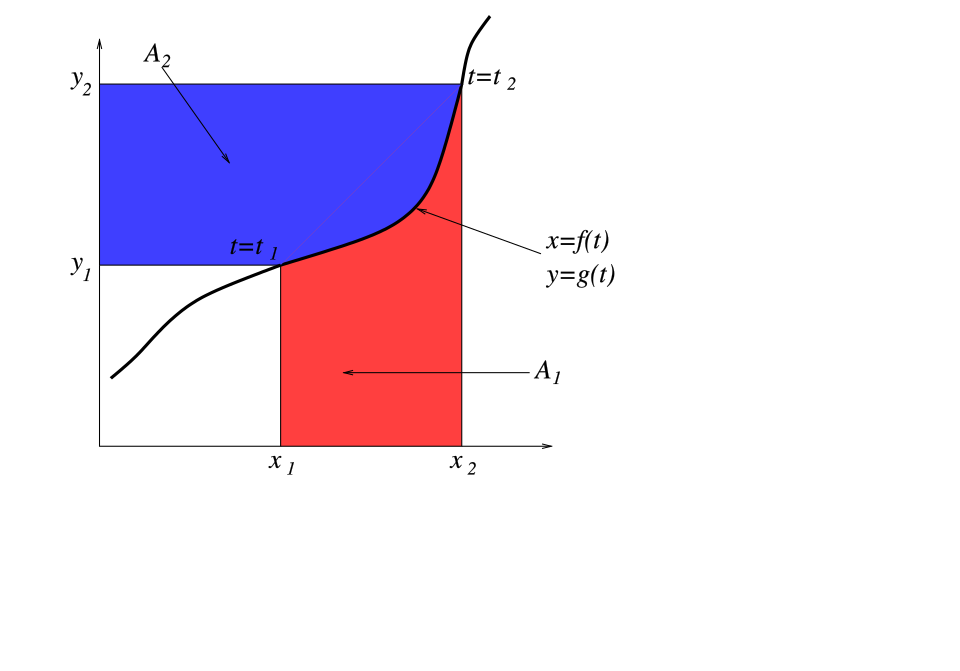
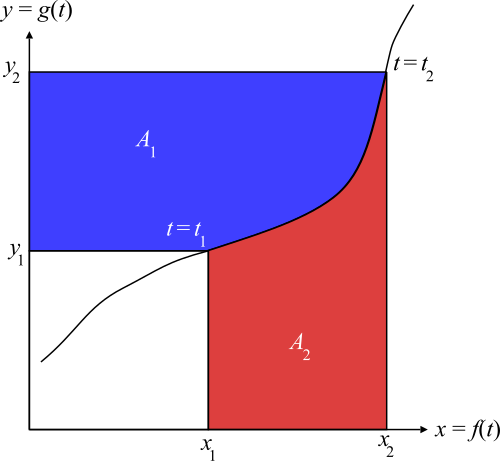
This geometric diagram visualizes integration by parts as a rearrangement of areas under a curve, illustrating why the identity is valid. It helps students see that different choices of and correspond to different ways of partitioning the same total area. The figure includes a bit more geometric detail than required by the syllabus, but all added structure supports intuition for the same integration by parts formula. Source.
FAQ
A good test is to mentally substitute your choices into the integration by parts structure and check whether the new integral is simpler than the original.
If the resulting integral contains more complicated expressions, new products, or additional functions you did not start with, your choice is likely counterproductive.
You can also compare the number of algebraic steps needed before and after differentiation or integration; if the count increases noticeably, reconsider your selection.
These functions typically become dramatically simpler when differentiated, often reducing to rational expressions.
This reduction frequently removes the most troublesome part of the integrand and leaves behind a more manageable product.
Because their antiderivatives are less straightforward, choosing them as dv would often make the problem considerably harder.
In such cases, test each option by briefly sketching the outcome:
• Differentiate each candidate for u and integrate the remaining part.
• Compare the resulting expressions to see which produces the simpler new integral.
• Consider whether the uv term will be easy to evaluate if used in a definite integral.
Sometimes the difference is small, and either choice may work, but one often leads to shorter algebraic manipulation.
When more than two functions are involved, decide which two will form the u and dv pairing and rewrite the expression accordingly.
A common strategy is:
• First identify the most difficult-to-integrate term and avoid selecting it as dv.
• Then identify the term that simplifies most when differentiated—this becomes u.
• Any remaining factors are grouped with dv as long as the combined expression is still easy to integrate.
This approach preserves the guiding principle of reducing the integral’s complexity.
Yes, some integrals require repeated applications, and your initial choices strongly influence whether the process converges smoothly.
When repetition is likely, choose u so that differentiating it repeatedly continues to simplify the expression in predictable steps.
Similarly, choose dv so that each integration step remains manageable and does not introduce new complications.
This forward-looking strategy prevents cycles and ensures that the process eventually terminates.
Practice Questions
Question 1 (1–3 marks)
Consider the integral ∫ x e^x dx.
(a) State a suitable choice of u and dv for applying integration by parts.
(b) Briefly explain why these choices simplify the integral.
Question 1 (1–3 marks)
(a) 1 mark for a correct identification of u = x and dv = e^x dx.
(b) 1–2 marks for a correct explanation such as:
Differentiating x simplifies it to 1.
Integrating e^x is straightforward.
The resulting integral is simpler than the original.
Question 2 (4–6 marks)
Let I = ∫ x ln(x) dx for x > 0.
(a) Choose u and dv appropriately and justify your choice.
(b) Use your selections to set up the integration by parts expression (do not evaluate the final integral).
(c) Explain how your choice ensures that the resulting integral is simpler than the original.
Question 2 (4–6 marks)
(a) 1–2 marks for correct choices and justification:
u = ln(x), dv = x dx.
Explanation: ln(x) differentiates to 1/x, greatly simplifying the expression, and x dx is easy to integrate.
(b) 1–2 marks for correctly setting up the integration by parts formula:u = ln(x), du = 1/x dx, v = x^2/2, so
I = (x^2/2) ln(x) - ∫ (x^2/2)(1/x) dx.
(c) 1–2 marks for a clear explanation that the new integral contains x rather than x ln(x), showing a reduction in complexity.

