Definite integrals using integration by parts extend the familiar technique for antiderivatives to integrals with limits, ensuring correct boundary evaluation and careful handling of the original interval.

Definite Integrals with Integration by Parts

Understanding the Purpose of Integration by Parts for Definite Integrals

Integration by parts is a method used to rewrite an integral of a product of functions into a more manageable form. It originates directly from the product rule for differentiation, which states that the derivative of a product involves two components. When reversed, this relationship allows one to replace a challenging integral with another integral that is simpler to compute while keeping the structure of the definite integral intact. For definite integrals, applying this technique requires special attention to the boundaries of the interval because these limits must be included in the final expression.

The product rule connection ensures that the method preserves the meaning of accumulated change inherent in definite integrals. As a result, integration by parts becomes an essential tool for integrals where one factor becomes simpler when differentiated and the other becomes easier to integrate.

A schematic summary of the integration by parts formula, showing how an integral of a product $u,dv$ is rewritten as $uv - \int v,du$. The labels on $u$, $du$, $v$, and $dv$ highlight the roles of differentiation and integration in the method. This visual directly supports the algebraic formula students apply when evaluating definite integrals by parts. Source.

The Integration by Parts Formula for Definite Integrals

The definite integral version of integration by parts mirrors the indefinite form but incorporates evaluation at the interval endpoints. This ensures that the accumulated change represented by the original integral is maintained within the new expression. The structure includes a boundary term, which captures the product of the chosen functions at the limits of integration. Understanding how this boundary term arises emphasizes why the formula must be applied carefully and systematically.

When choosing $u$ and $dv$, students generally follow a strategy similar to the one used in indefinite integration by parts: select $u$ as the expression that becomes simpler when differentiated, and choose $dv$ to be easily integrable. The definite integral form ensures the limits appear only after integrating $dv$ to obtain $v$, preserving the connection to the original interval.

Importance of Boundary Evaluation

In definite integration by parts, the term $\left[u,v\right]_a^b$ must always be evaluated before computing the remaining integral. This evaluation ensures that the total accumulated change is represented correctly. Because integration by parts transforms the integral but does not change its meaning, the boundary term plays a crucial role in completing the calculation.

Key considerations when evaluating the boundary term include:

• Ensuring that both $u$ and $v$ are defined and continuous on the interval.

• Substituting the limits after obtaining an explicit expression for $v$.

• Computing $u(b)v(b) - u(a)v(a)$ with precise attention to signs and grouping.

A failure to evaluate this boundary term properly leads to incorrect results, even when the remaining integral is computed correctly. The accuracy of the final answer depends equally on boundary evaluation and on the transformation of the integral itself.

Preserving the Limits of Integration

A defining feature of this subsubtopic is the emphasis on maintaining the original limits of integration throughout the process. Unlike substitution for definite integrals—where changing variables requires adjusting the bounds—integration by parts relies on the original variable, meaning the limits remain unchanged. This simplifies the process but requires care when handling the differential expressions.

To preserve the limits effectively:

• Keep $a$ and $b$ attached to the integral symbol in every step.

• Avoid prematurely inserting numerical values into $u$ or $v$ before computing the boundary term.

• Rewrite $\int_a^b v,du$ directly in terms of $x$ without altering the bounds.

Students often make errors by mixing evaluated expressions with unevaluated integrals. Keeping symbolic expressions intact until the correct evaluation step prevents confusion and ensures logical consistency.

Strategic Use of Integration by Parts

When deciding to apply integration by parts for a definite integral, students should verify that the method simplifies the integrand and reduces the problem to a more elementary integral. Effective use involves recognizing patterns indicating that one function becomes easier when differentiated while the other integrates smoothly. This strategic recognition aligns the method with the goal stated in the syllabus: applying the technique in a way that preserves structure and leads to successful evaluation.

Common strategic tips include:

• Choose $u$ to become simpler after differentiation.

• Select $dv$ so that $v$ does not introduce additional complexity.

• Ensure the resulting integral $\int_a^b v,du$ is simpler than the original.

• Remember that the boundary term may contribute significantly to the final value.

A consistent, organized approach ensures that integration by parts becomes a reliable method for evaluating definite integrals, especially in cases involving products of polynomial, exponential, or logarithmic expressions.

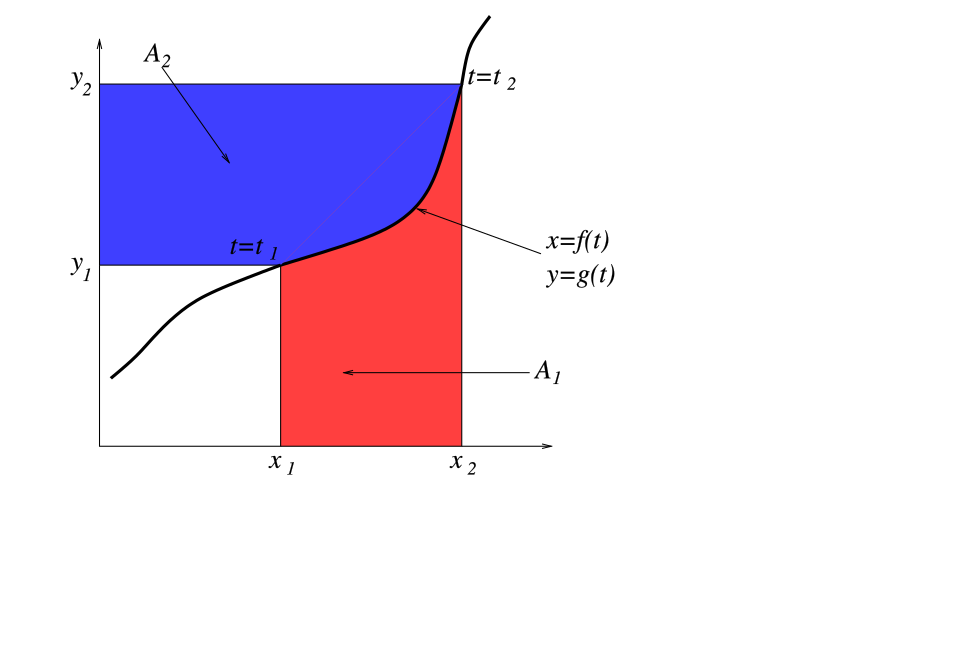
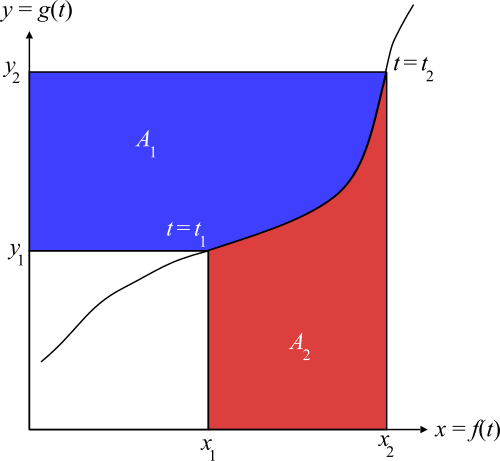
A geometric diagram illustrating integration by parts by comparing shaded regions whose areas are algebraically equivalent. The picture shows how rearranging these areas corresponds to rewriting an integral of a product as a boundary term minus a new integral. The figure contains additional proof-oriented detail beyond the AP syllabus but still supports conceptual understanding of the formula. Source.