Writing differential equations from real-world descriptions requires carefully identifying how quantities change and translating verbal phrases about rates into precise mathematical notation that captures these relationships.

Understanding the Goal of Translating Verbal Statements

When a problem describes how one quantity changes with respect to another, it provides the essential information needed to express a differential equation. A differential equation relates an unknown function to its derivative, and your task in this subsubtopic is to convert verbal statements into symbolic form.

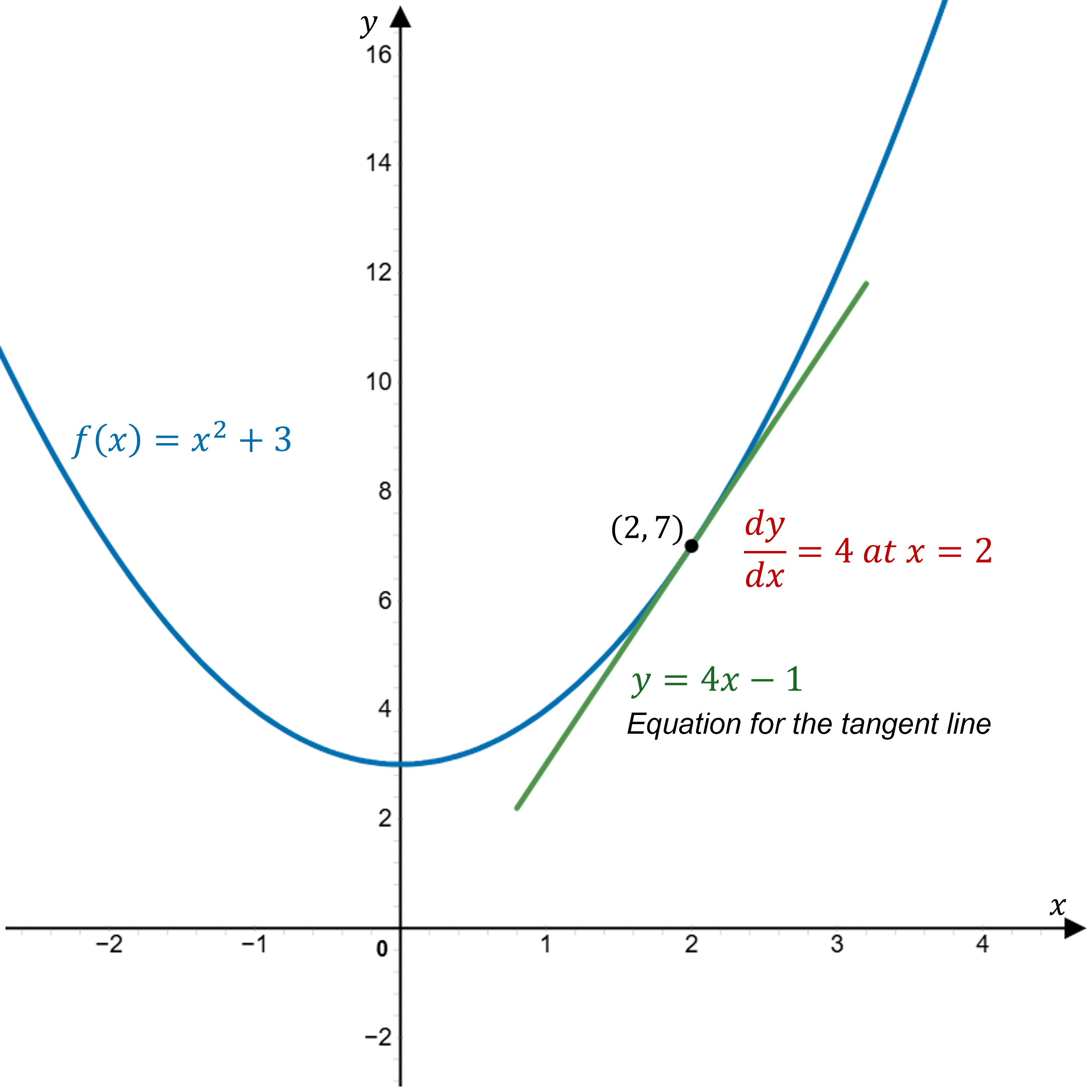
A graph of the function $f(x)=x^2+3$ (blue) with a tangent line at $x=2$ (green), illustrating that the derivative gives the slope of the tangent. This highlights how geometric “rate of change” corresponds to symbolic derivative notation. The visual reinforces how verbal phrases about change translate into differential equations. Source.

Identifying Change Descriptions in Context

Verbal descriptions typically contain phrases that signal a rate relationship. These phrases correspond directly to derivative expressions that express how the dependent variable changes relative to the independent variable.

Common Rate Phrases and Their Meanings

Students must recognize that certain wording almost always indicates a derivative relationship. Such phrases guide the construction of the appropriate derivative expression.

• “Rate of change of…” translates to a derivative like $dy/dt$ or $dP/dx$.

• “Increases (or decreases) at a rate proportional to…” suggests the rate depends on the current value of the quantity.

• “With respect to…” identifies the independent variable in the rate relationship.

• “Is given by…” indicates that the following expression defines the rate.

These linguistic cues help determine both the structure and the variables involved in the differential equation.

Naming the Independent and Dependent Variables

A differential equation must clearly indicate which quantity depends on which. The independent variable is the variable with respect to which change is measured, while the dependent variable is the quantity whose change is being described.

After defining the independent variable, the dependent variable naturally becomes the function whose behavior is modeled. This choice should always match the wording of the context, such as “time” acting as the input when describing how a population evolves.

A sentence must follow here to maintain proper spacing before another definition.

Connecting Verbal Descriptions to Derivative Notation

Once variables are identified, students convert the statement about how the quantity changes into an appropriate derivative expression. This step requires careful interpretation to ensure the mathematical relationship accurately reflects the verbal meaning.

Translating Verbal Phrases to Derivatives

Constructing the differential equation typically involves two tasks: determining the correct derivative and expressing the relationship the problem provides.

• Identify the verb describing change (such as “changes,” “increases,” “decreases”).

• Determine what the rate depends on—the dependent variable, another function, or a constant.

• Decide whether the relationship describes a direct equality, a proportional relationship, or a more complex dependency.

Building the Differential Equation Structure

Once the derivative is established, it must be set equal to the expression specified by the context. This translation process turns descriptive language into symbolic form.

Symbolic Representation of Rate Information

The general structure of differential equations constructed in this subsubtopic follows the format:

A normal sentence helps maintain clarity before continuing with further conceptual detail.

The expression on the right side of the equation must be chosen to reflect the relationships described verbally. For example, if a statement says a quantity “decreases at a constant rate,” the rate expression should be a constant with an appropriate sign to indicate decrease.

Ensuring That the Differential Equation Matches the Context

The completed differential equation should fully reflect the meaning of the original verbal description. Misinterpreting wording or mixing up dependent and independent variables leads to an equation that does not accurately represent the situation.

Checklist for Constructing Accurate Differential Equations

Students can verify correctness by reviewing key elements:

• Variable identification: Do the chosen variables match the wording and context?

• Derivative structure: Does the derivative correctly represent the rate of change described?

• Expression accuracy: Does the rate expression capture proportionality, constancy, or dependence on another variable as stated?

• Consistency of units: Are the derivative and its corresponding rate expression dimensionally consistent?

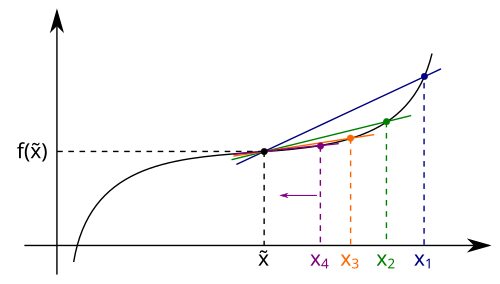
A smooth curve with two marked points and a secant line illustrates the average rate of change approaching the derivative as the interval shrinks. The labeled $\Delta x$ and $\Delta y$ reinforce how derivatives measure change with respect to another variable. This diagram includes minor additional limit-definition context but directly supports interpreting verbal “rate of change” statements as derivatives. Source.

This careful interpretation ensures that the symbolic differential equation reflects the verbal description accurately and prepares students for subsequent problem-solving steps involving initial conditions or solution techniques.