Understanding how general solutions and particular solutions relate is essential for interpreting differential equations, because additional conditions transform broad families of functions into specific, meaningful results within real-world contexts.

General and Particular Solutions in Differential Equations

The Role of Integration in Producing General Solutions

When solving a first-order differential equation, integration is typically used to reverse differentiation and recover the original unknown function. This process inherently introduces an arbitrary constant, commonly written as $C$, because many functions share the same derivative. The presence of this constant means the solution represents not a single function, but an entire family of functions that satisfy the differential equation.

The general solution communicates all mathematically possible solution curves without specifying which one corresponds to a particular scenario or condition. Because differential equations often model real processes, the general solution serves as the broad theoretical form from which meaningful, context-dependent solutions can later be extracted.

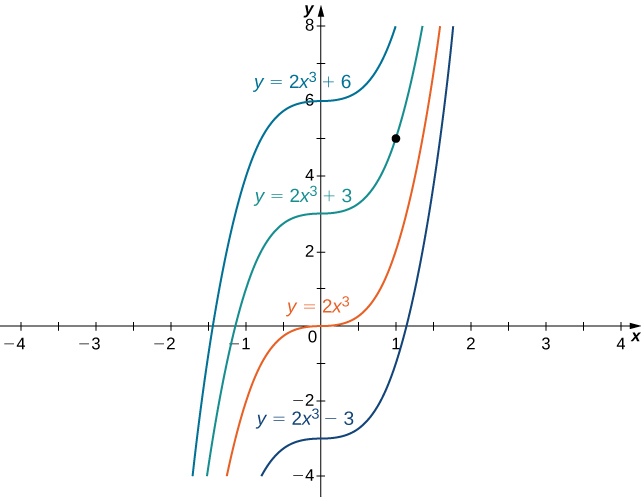
This graph shows several solution curves of the differential equation $\frac{dy}{dx}=6x^2$, each corresponding to a different value of the constant $C$ in the general solution $y=2x^3+C$. The highlighted curve $y=2x^3+3$ is the particular solution that passes through the initial condition $y(1)=5$. This visual emphasizes that the general solution is a family of curves, whereas a particular solution is the single curve that satisfies both the differential equation and a specified condition. Source.

After presenting the general solution, it becomes essential to understand how additional information selects one specific member of this family.

When General Solutions Are Appropriate

A general solution is typically the final result when the problem requires describing all possible behaviors allowed by the differential equation. These solutions are especially useful when:

• Multiple physical or theoretical scenarios share the same rate relationship.

• The problem does not supply any condition to narrow down to a single curve.

• The goal is to analyze the structural form of solutions rather than compute a unique value.

In these cases, leaving the constant $C$ undetermined preserves the entire set of valid possibilities.

Introducing Particular Solutions

A particular solution arises when extra information, such as an initial value or a specified point on the solution curve, is provided. This additional information allows one to solve for the previously arbitrary constant, reducing the general family to one unique function.

Between the differential equation and an initial condition, the resulting particular solution becomes fully determined and corresponds to a single graph on the coordinate plane, rather than a family of possible curves.

A typical initial condition takes the form $y(x_0)=y_0$, and it provides a specific point through which the solution curve must pass. By substituting this into the general solution, one determines the constant of integration.

The Relationship Between General and Particular Solutions

The connection between these two forms is central to differential equations:

• The general solution expresses all functions that satisfy the differential equation.

• A particular solution identifies exactly one function from that family using extra conditions.

• Initial conditions serve as constraints that eliminate all but one member of the solution set.

This structure parallels the broader mathematical theme of moving from a general representation to a specific instance once sufficient information is known.

Using Equations to Show the Structure of Families and Specific Choices

To clarify the relationship, it is often helpful to express the general and particular solutions symbolically.

A single sentence between blocks ensures clear spacing before the next formal expression.

These symbolic structures reinforce that the differential equation alone is insufficient to determine a unique function, but the addition of conditions yields a fully defined solution.

Why Distinguishing Between These Solutions Matters

Understanding the distinction between general and particular solutions is crucial for interpreting the meaning of a differential equation within context. Many real-world situations—such as motion, population change, or thermodynamic processes—require not only a rate relationship but also an initial state to produce a meaningful prediction or description.

Some key reasons this distinction is essential include:

• Model specificity: Real scenarios typically start at a known initial condition, making the general solution incomplete without further information.

• Interpretable graphs: Slope fields and solution curves represent families of solutions; initial conditions select one precise curve.

• Predictive accuracy: Only a particular solution allows direct computation of the function’s value at later points.

Situations Where Only One Form Is Needed

Students should recognize whether a situation calls for a general or particular solution:

• If the problem requests “the general solution,” the answer should retain $C$.

• If an initial condition is given, the goal is almost always to find the particular solution.

• If the context involves describing all possible behaviors, the general form is appropriate.

Conceptual Summary of Their Relationship

The general solution provides the broad structure of all functions satisfying the differential equation, and particular solutions emerge when additional information restricts the family to a single curve. On a graph, every choice of initial point singles out exactly one solution curve from the general family, visually reinforcing the idea that particular solutions are context-driven selections rather than entirely new functions.

This figure contrasts a general solution, shown as many curves compatible with a differential equation, with a particular solution, shown as a single curve passing through a specified initial point. The background slope field indicates how each solution curve follows identical local slope information. The slope field itself is a concept developed later, but here it reinforces that infinitely many solutions exist while an initial condition selects exactly one. Source.