AP Syllabus focus:
‘A slope field is a graphical representation of a first-order differential equation on a finite grid of points, where each point shows a small line segment with slope given by the differential equation.’
Slope fields offer a visual method for understanding differential equations by displaying small line segments whose slopes represent instantaneous rates of change, revealing solution behavior without algebraic solving.
Understanding What a Slope Field Represents
A slope field provides a picture of how solutions to a first-order differential equation behave by showing many tiny line segments at selected points in the plane. Each segment’s orientation reflects the slope specified by the differential equation. This approach allows students to analyze differential equations qualitatively, gaining insight into how solutions change even when finding an explicit formula is difficult or impossible.

This diagram shows a slope field for the differential equation , with each line segment representing the slope of a solution at that point. Regions where is positive or negative produce corresponding upward or downward orientations. The inclusion of the specific function extends slightly beyond the syllabus but remains appropriate for AP Calculus AB. Source.
Slope Field: A graphical diagram of short line segments drawn at specific points, each segment having slope equal to the value of a given first-order differential equation at that point.
Slope fields help students connect symbolic derivative expressions with the geometric behavior of solution curves. Instead of computing explicit functions, students interpret the overall pattern of slopes to infer the shape and tendencies of possible solutions.
First-Order Differential Equations and Local Behavior
A slope field corresponds to a first-order differential equation, which relates a function to its first derivative . The slope of each segment in the field is determined by evaluating the derivative expression at that point. Because the field shows slopes everywhere, it reveals the local behavior of all possible solutions.
First-Order Differential Equation: An equation involving an unknown function and its first derivative but no higher derivatives.
The idea of local behavior is central: each small segment approximates the slope of the tangent to a solution curve at a point. When these segments are viewed collectively, they illustrate how solutions evolve across the plane.
How Slope Fields Are Constructed Conceptually
Although technology often generates slope fields automatically, understanding their construction strengthens comprehension. The process relies on the derivative expression dictating the slope at each point.
Essential Steps Behind a Slope Field
Identify the differential equation, typically written in the form , which indicates the slope at every point .
Choose a grid of points in the plane where slopes will be computed.
Evaluate the derivative expression at each point to determine the slope.
Draw a short, centered line segment at each point with the corresponding slope.
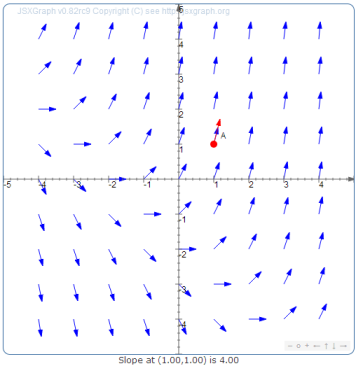
This figure shows a slope field for , with each blue arrow indicating the locally defined slope at its grid point. It visually reinforces the process of assigning slopes to all points to form a complete slope field. The red point and numerical slope displayed come from the interactive software and are not required for AP Calculus AB. Source.
Even without explicitly drawing, recognizing that each segment’s slope comes from the differential equation helps students interpret a completed slope field more effectively.
= Derivative value specifying slope at point
These slopes reveal whether solutions increase, decrease, flatten, or steepen as they pass through different regions.
Interpreting the Visual Features of Slope Fields
Slope fields communicate several types of qualitative information about differential equations. A student analyzing a slope field can observe distinct patterns that illustrate how solutions behave.
Key Visual Features Students Should Recognize
Regions of consistent slope: Indicate areas where solutions rise or fall steadily.
Horizontal segments: Suggest points where , often hinting at equilibrium behavior.
Changes in slope direction: Reflect how the rate of change varies across the plane.
Families of potential solution curves: Though not drawn directly, curves can be mentally sketched by following the orientation of adjacent slope segments.
Because slope fields show many possible solution paths simultaneously, they reinforce the idea that a differential equation typically admits a family of solutions, not just one.
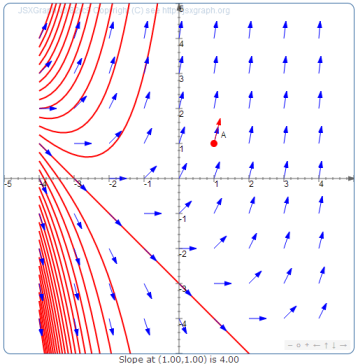
This diagram presents the same slope field for along with multiple red solution curves that remain tangent to the blue arrows. It illustrates how different initial conditions generate a family of solutions to the same differential equation. The red point and dynamic labels originate from the applet and exceed what is needed for AP settings. Source.
Why Slope Fields Matter in Differential Equations
Slope fields play an important conceptual role in AP Calculus AB because they allow students to understand differential equations without solving them analytically. Many real-world models produce equations that are difficult or impossible to solve explicitly. Slope fields provide an accessible way to infer long-term tendencies, stability, or solution shape from the geometry of slopes alone.
Conceptual Benefits for Students
They reveal how the derivative governs the direction of solutions at every point.
They provide intuitive understanding of solution behavior before applying algebraic techniques.
They emphasize the connection between rate of change and graphical behavior, reinforcing the meaning of the derivative in a functional context.
They prepare students for later work involving initial conditions, particular solutions, and qualitative reasoning.
Through visualizing how solutions evolve, slope fields strengthen comprehension of differential equations as dynamic relationships rather than purely symbolic expressions.
FAQ
A slope field depending only on x will show vertical bands of identical slope, since the slope is the same for all points with the same x-value.
A slope field depending only on y will show horizontal bands of identical slope, because the slope is constant along each horizontal line.
If neither pattern appears, the slope likely depends on both variables.
Autonomous equations depend only on the dependent variable y, not on x. This means that slopes remain constant along horizontal lines.
Such fields often display equilibrium solutions where the slope is zero and nearby solutions indicate whether points above or below move toward or away from these lines.
In well-behaved first-order differential equations, slope fields show that solution curves cannot cross.
If two curves were to intersect, they would share the same point but have different slopes, violating the rule that the slope at a given point in the field is uniquely defined.
Look for regions where the line segments become very steep. Steepness signals that the rate of change increases dramatically in that part of the plane.
Rapid growth corresponds to strongly upward-tilted segments; rapid decay corresponds to strongly downward-tilted ones.
If these steep regions cluster, solutions may rise or fall quickly when passing through them.
Patterns of segment orientations often hint at overall movement.
Converging slopes suggest that solutions may stabilise toward a common path or equilibrium.
Diverging slopes indicate solutions moving apart, signalling sensitive dependence on initial conditions.
Extended regions of nearly horizontal slopes reveal intervals where change is slow.
These visual cues allow prediction of general solution behaviour without explicit solving.
Practice Questions
Question 1 (1–3 marks)
A slope field for the differential equation dy/dx = f(x, y) is shown on a grid. At the point (1, 2), the short line segment in the slope field appears to have a positive, moderately steep slope.
(a) State what this indicates about the value of dy/dx at the point (1, 2).
(b) Explain briefly what this implies about the behaviour of a solution curve passing through (1, 2).
Question 1
(a) 1 mark:
• States that dy/dx at (1, 2) is positive and of moderate size (e.g., “dy/dx is positive and moderately steep”).
(b) 1–2 marks:
• 1 mark for stating that a solution curve passing through (1, 2) would be increasing at that point.
• 1 mark for stating that the curve’s tangent at (1, 2) has the same positive slope as shown in the field.
Total: 2–3 marks
Question 2 (4–6 marks)
A slope field is drawn for a first-order differential equation.
(a) Describe the steps required to construct such a slope field by hand.
(b) The slope field includes a horizontal row of line segments with slope zero. Explain what this indicates about the differential equation and the possible behaviour of solution curves in that region.
(c) A student claims that a slope field represents only one solution curve. Explain why this is incorrect.
Question 2
(a) 2–3 marks:
• 1 mark for stating that the differential equation dy/dx = f(x, y) must be evaluated at each chosen grid point.
• 1 mark for describing that short line segments are drawn at each point with the corresponding slope.
• 1 mark for mentioning use of a grid of regularly spaced points.
(b) 1–2 marks:
• 1 mark for explaining that slope zero indicates dy/dx = 0 at those points.
• 1 mark for noting that solutions will be momentarily horizontal or may approach equilibrium behaviour in that area.
(c) 1 mark:
• Correctly states that a slope field shows many possible solution curves, each determined by different initial conditions, not a single unique solution.
Total: 4–6 marks

