Rectangular cross-sectional solids arise when a plane region serves as a base and every slice perpendicular to an axis forms a rectangle whose dimensions vary with position.

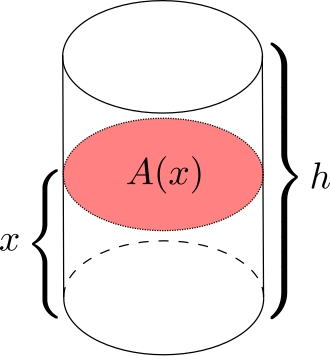
This diagram shows a cylinder with a thin slice taken at position $x$, whose cross-sectional area is denoted $A(x)$. It illustrates how volume arises from integrating an area function along an axis. In rectangular cross-section problems, $A(x)$ corresponds to a rectangle rather than a circle. Source.

Understanding Rectangular Cross Sections

A rectangular cross section is formed when a solid is built by stacking infinitely many thin rectangles perpendicular to either the x-axis or the y-axis. The key idea is that each slice has an area determined by a variable width and height, both of which depend on the position along the chosen axis of integration. This subsubtopic emphasizes how geometric attributes of the slices can be expressed using known bounding functions of the base region.

When working with such solids, AP Calculus AB students need to identify which direction the slices are taken, determine the dimensions of each rectangle, and express these dimensions as functions that can be integrated to accumulate total volume.

Base Regions and Orientation

The base region of the solid is a two-dimensional area in the coordinate plane bounded by one or more curves. This base determines where rectangular slices are taken. The orientation of the slices—perpendicular to the x-axis or the y-axis—dictates both the variable of integration and how the dimensions of the rectangles are expressed.

• If slices are perpendicular to the x-axis, their width is $dx$, and their height is determined by the vertical distance between bounding curves evaluated at a given x-value.
• If slices are perpendicular to the y-axis, their width is $dy$, and their height is determined by the horizontal distance between bounding curves evaluated at a given y-value.

Before any formula is written, students must understand how the geometry of the region influences which dimensions apply to each rectangle.

Determining Rectangle Dimensions

Each rectangular slice has two dimensions: a base length (sometimes called breadth) determined by the region’s boundaries, and a height that may come from a geometric description or contextual model. These dimensions typically vary along the axis of integration.

In many problems, the height is given directly as a function such as $h(x)$ or $h(y)$, while the base length must be derived from the difference of two bounding functions. In other scenarios, the height may be constant or determined by contextual conditions involving the underlying geometry.

Because rectangular cross sections are highly adaptable, a problem may use any combination of functions to define the rectangle’s dimensions. What remains consistent is that both dimensions must be expressible in terms of the variable of integration.

Area of a Rectangular Slice

The area of each infinitesimally thin rectangular slice is the product of its variable height and variable base length. This must be written in the correct variable before constructing the definite integral that yields the volume.

The expression for $A(x)$ or $A(y)$ depends strictly on the geometry of the region, and students must carefully link all dimensions to the appropriate variable. A common source of error is mixing variables or using inconsistent functions; each dimension must be written exclusively in terms of x when integrating with respect to x, or exclusively in terms of y when integrating with respect to y.

After determining the expression for slice area, a student is ready to construct the volume integral. This step relies on understanding that the definite integral accumulates infinitely many rectangular slice areas to form the entire solid.

Volume as Accumulated Rectangle Areas

Rectangular cross-section problems rely on interpreting volume as accumulated area. Because a solid is built from layered rectangles, the definite integral computes the total volume by summing their areas across the domain of integration.

This expression reinforces the view of integration as an accumulation process, consistent with other applications of integrals in the AP Calculus AB curriculum. When using $dy$, the formula is analogous, with corresponding adjustments to the rectangle dimensions and the limits of integration.

A complete setup must include:
• Clear identification of the interval over which rectangles are taken.
• Correct expressions for both rectangle dimensions based on bounding curves or context.
• A properly constructed integrand that reflects the product of base length and height.
• Integration with respect to the variable aligned with slice orientation.

Applications of Rectangular Cross Sections

Rectangular cross sections appear not only in pure geometric constructions but also in modeling contexts where physical or conceptual constraints produce variable rectangular shapes. In applied scenarios, functions may represent measurements such as widths of containers, cross-sectional profiles of beams, or changing dimensions of manufactured objects.

Common application considerations for AP students include:
• Extracting geometric dimensions from verbal descriptions and translating them into variable expressions.
• Determining whether dimensions change linearly or nonlinearly with position along the axis.
• Recognizing that all modeling assumptions must be represented in the area expression for each rectangular slice.

These applications underscore the importance of interpreting functions as representations of varying physical quantities. Understanding how rectangular cross sections capture these variations is essential for successfully constructing and evaluating volume integrals in diverse settings.

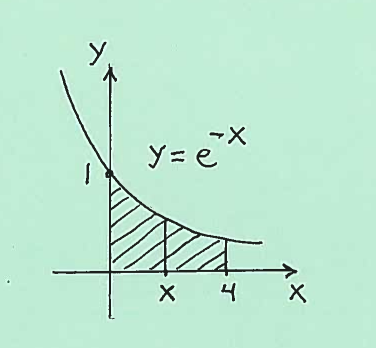
This sketch shows a solid with a base in the $xy$-plane and a vertical rectangular slice at a chosen value of $x$. It demonstrates how a boundary curve determines the height of each slice. The original example uses square cross sections, a special case of rectangular sections. Source.