Understanding moles and molar mass is essential for accurately quantifying substances in chemical reactions. These concepts let us count particles by weighing them, bridging the gap between the atomic world and the macroscopic world of laboratory measurements.
The Atom: Building Block of Matter
Before exploring moles, we need a basic understanding of the atom, which is the smallest unit of an element that retains its properties. Atoms are incredibly small—far too small to see or count individually—but their structure helps explain why the mole concept is needed.
Each atom consists of three types of subatomic particles:
Protons: Positively charged particles located in the nucleus.
Neutrons: Neutral particles also located in the nucleus.
Electrons: Negatively charged particles that orbit the nucleus in energy levels or shells.

Image Courtesy of Let's Talk Science. There are different models of an atom, but the above is an example of where subatomic particles may exist.
The nucleus is the dense central core of an atom. Since it contains both protons and neutrons, it holds nearly all of the atom’s mass and has a net positive charge. The much lighter electrons orbit around this nucleus. The structure of an atom determines how it behaves chemically, but due to their minuscule size, counting atoms one by one is impossible. This is why chemists developed the concept of the mole—to work with atoms in measurable amounts.
What Is a Mole?
A mole is a counting unit in chemistry, just like a dozen represents 12 items. But instead of 12, a mole represents a far larger number:
1 mole = 6.022 × 10^23 particles
This number is called Avogadro’s number. It tells us how many particles—atoms, molecules, ions, or other units—are present in one mole of a substance. For example:
1 mole of oxygen atoms contains 6.022 × 10^23 atoms of oxygen.
1 mole of water molecules contains 6.022 × 10^23 water molecules.
This large quantity is necessary because atoms and molecules are so small that laboratory quantities of substances contain astronomical numbers of particles. Using moles lets scientists perform calculations involving large numbers of atoms with ease and precision.
Importance of Moles in Biology and Chemistry
The mole concept is foundational for:
Determining quantities of substances involved in reactions.
Calculating concentrations in solutions.
Balancing chemical equations to predict product amounts.
Converting between mass, volume, and particle numbers.
In biological systems, moles help describe concentrations of ions, nutrients, enzymes, and gases—making them essential for understanding processes like cell respiration, photosynthesis, and DNA replication.
Molar Mass: Definition and Use
Molar mass is the mass of one mole of a substance, expressed in grams per mole (g/mol). It allows conversion between grams and moles.
For elements, the molar mass is the same as the atomic mass (from the periodic table), but in units of grams per mole instead of atomic mass units (amu).
For compounds, molar mass is the sum of the atomic masses of all atoms in the formula.
For example:
The atomic mass of hydrogen is approximately 1.008 amu, so its molar mass is 1.008 g/mol.
The atomic mass of oxygen is about 16.00 amu, so its molar mass is 16.00 g/mol.
Knowing molar mass lets you convert grams to moles or moles to grams—an essential skill for chemical calculations.

This is the periodic table that will be provided for you during the AP Chemistry Exam. You may access it online here.
How to Calculate Molar Mass
To calculate the molar mass of a compound:
Identify the elements in the compound.
Determine the number of atoms of each element from the chemical formula.
Find the atomic mass of each element using the periodic table.
Multiply each atomic mass by the number of atoms.
Add all values together to get the compound’s molar mass.
Example: Water (H2O)
Water contains:
2 hydrogen atoms: 2 x 1.008 g/mol = 2.016 g/mol
1 oxygen atom: 1 x 16.00 g/mol = 16.00 g/mol
Molar mass of water = 2.016 + 16.00 = 18.02 g/mol
This means that 1 mole of water weighs 18.02 grams.
Example: Carbon Dioxide (CO2)
CO2 contains:
1 carbon atom: 1 x 12.01 g/mol = 12.01 g/mol
2 oxygen atoms: 2 x 16.00 g/mol = 32.00 g/mol
Molar mass of CO2 = 12.01 + 32.00 = 44.01 g/mol
So, one mole of carbon dioxide has a mass of 44.01 grams.
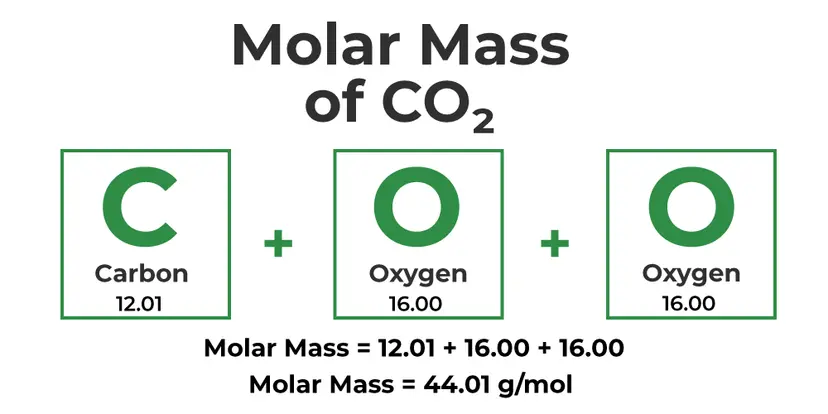
Image Courtesy of GeeksforGeeks
Avogadro’s Number and the Mole-Particle Relationship
Avogadro’s number (6.022 × 10^23) lets us convert between moles and particles. This relationship is used to:
Find the number of atoms or molecules in a given amount of substance.
Determine how many particles are in one mole.
Predict the number of atoms of a specific element within a compound.
Example: Molecules in 1.14 moles of CO2
Multiply the number of moles by Avogadro’s number:
1.14 moles x 6.022 × 10^23 molecules/mole = 6.87 × 10^23 molecules of CO2
So, 1.14 moles of CO2 contains approximately 6.87 × 10^23 molecules.
Counting Individual Atoms in a Compound
Chemical formulas tell us the ratio of atoms in a molecule. For example:
CO2 has 1 carbon atom and 2 oxygen atoms per molecule.
If we know the number of molecules, we can find the number of individual atoms.
Carbon Atoms in CO2
From the previous example: 6.87 × 10^23 molecules of CO2
Each CO2 has 1 carbon atom
Carbon atoms = 6.87 × 10^23 × 1 = 6.87 × 10^23 atoms of carbon
Oxygen Atoms in CO2
Each CO2 has 2 oxygen atoms
Oxygen atoms = 6.87 × 10^23 × 2 = 1.37 × 10^24 atoms of oxygen
This is useful for interpreting biological molecules like carbohydrates, nucleic acids, and proteins, where atomic compositions matter.
Dimensional Analysis: Converting Between Units
Dimensional analysis is a method for converting between units using conversion factors. It helps ensure that units cancel appropriately and that the result is in the desired unit.

Dimensional analysis is going to be so useful throughout this course, especially when you forgot a formula that is essential to solving the question!
Common Conversion Factors in Chemistry:
Molar mass: g/mol
Avogadro’s number: 6.022 × 10^23 particles/mole
Step-by-Step: Grams to Moles
Convert 50.0 grams of CO2 to moles:
Identify the molar mass: CO2 = 44.01 g/mol
Use the formula:
Moles = mass (g) / molar mass (g/mol)
Moles = 50.0 g / 44.01 g/mol = 1.136 moles of CO2
The grams cancel out, leaving moles.

Step-by-Step: Moles to Molecules
Convert 1.14 moles of CO2 to molecules:
Use Avogadro’s number as the conversion factor.
Multiply:
1.14 moles x 6.022 × 10^23 molecules/mole = 6.87 × 10^23 molecules
The moles cancel, and the result is in molecules.

Step-by-Step: Molecules to Atoms
Use the subscripts in the formula to find how many of each atom is present.
CO2 contains 2 oxygen atoms per molecule.
Oxygen atoms = 6.87 × 10^23 molecules × 2 = 1.37 × 10^24 atoms

You can repeat this for any compound with known molecular formula.
Tips for Using Dimensional Analysis
Always write down units and make sure they cancel.
Set up your conversion as a series of ratios.
Keep track of significant figures in your calculations.
Use known relationships:
1 mole = 6.022 × 10^23 particles
Molar mass (g/mol) from the periodic table
Key Equations to Remember
These are essential for solving mole-related problems:
Moles = Mass (g) / Molar Mass (g/mol)
Mass (g) = Moles × Molar Mass (g/mol)
Particles = Moles × Avogadro’s Number (6.022 × 10^23)
Atoms = Molecules × Subscript in chemical formula
Each of these formulas allows you to convert between mass, moles, molecules, and atoms depending on what information is given and what is required.
Vocabulary for Mastery
Atom: The smallest unit of an element that retains its properties.
Mole: A unit that represents 6.022 × 10^23 particles.
Avogadro’s Number: The number of particles in one mole.
Molar Mass: The mass of one mole of a substance, in g/mol.
Atomic Mass: The weighted average mass of an atom’s isotopes, in amu.
Chemical Formula: A representation of a molecule that shows the types and numbers of atoms.
Subscript: The small number in a chemical formula that tells how many atoms of each element are present.
Dimensional Analysis: A method of converting between units using conversion factors.
Conversion Factor: A ratio used to convert one unit to another.
Periodic Table: A chart of elements arranged by atomic number, used to find atomic masses.
Grams per Mole (g/mol): The unit of molar mass, showing how many grams are in one mole of a substance.
Mass: The amount of matter in a substance, often measured in grams.
Particles: Atoms, molecules, or ions that make up substances.
Subatomic Particles: Protons, neutrons, and electrons within an atom.
FAQ
Molar mass is rarely a whole number because it represents the average atomic mass of all the naturally occurring isotopes of an element, each with its own mass and natural abundance. Elements often exist as a mixture of two or more isotopes in nature. For example, chlorine exists mainly as two isotopes: chlorine-35 and chlorine-37. The molar mass shown on the periodic table (approximately 35.45 g/mol for chlorine) reflects the weighted average of these isotopes. This ensures calculations based on molar mass are accurate for real-world samples, not just idealized atomic forms.
Molar mass = average of isotope masses × their relative abundances
Explains why most atomic masses have decimal values
Ensures laboratory measurements align with naturally occurring samples
To calculate the molar mass of a compound containing polyatomic ions or grouped atoms in parentheses, follow these steps:
Identify all atoms in the compound, including those within parentheses.
Multiply the atoms inside the parentheses by the subscript that follows.
Use the periodic table to find each element’s atomic mass.
Multiply each atomic mass by the total number of atoms and add everything together.
For Ca(NO3)2:
Ca: 1 × 40.08 = 40.08 g/mol
N: 2 × 14.01 = 28.02 g/mol
O: 6 × 16.00 = 96.00 g/mol
Total = 40.08 + 28.02 + 96.00 = 164.10 g/mol
This method ensures correct stoichiometric calculations.
While often used interchangeably, molar mass and molecular mass differ in context and units:
Molar mass is the mass of one mole of a substance, expressed in grams per mole (g/mol). It is used in laboratory calculations and for converting between mass and moles.
Molecular mass is the mass of a single molecule, calculated in atomic mass units (amu). It is more theoretical and used for describing molecules at the atomic level.
Use molar mass when measuring real substances and conducting experiments. Use molecular mass when referring to individual molecules in theoretical or microscopic discussions.
Molar mass = practical, used in labs
Molecular mass = theoretical, used in atomic-scale analysis
The mole concept is essential for working with macromolecules such as proteins, nucleic acids, and polysaccharides, even though their structures are complex:
Each molecule of a protein or DNA strand has a specific molecular formula, allowing calculation of its molar mass.
One mole of a protein corresponds to 6.022 × 10^23 protein molecules.
Calculations based on molar mass allow scientists to determine how much of a substance to use in reactions such as enzyme assays or PCR.
This is especially important in biochemistry and molecular biology, where concentrations of large molecules must be precisely known for reactions to function correctly.
No, the molar mass of a substance does not change with variations in temperature or pressure because it is an intrinsic property of the substance based on the mass and number of atoms in its formula. Molar mass is determined solely by the atomic masses of the elements involved and their quantities in a compound.
However, density and volume of gases may change with temperature and pressure.
For gases, the ideal gas law (PV = nRT) is used to relate molar mass with measurable properties like pressure and temperature.
In solids and liquids, phase changes may occur, but the identity and molar mass remain constant.
Practice Questions
A biologist measures out 36.04 grams of water (H2O) for a cellular respiration experiment. Calculate the number of moles of water used, and determine how many water molecules this sample contains. Show your reasoning.
To find the number of moles, divide the mass by the molar mass of water. The molar mass of water is 18.02 g/mol, so 36.04 g ÷ 18.02 g/mol = 2.00 moles of water. To determine the number of molecules, multiply the moles by Avogadro’s number: 2.00 moles × 6.022 × 10^23 molecules/mole = 1.204 × 10^24 molecules of water. This calculation allows the biologist to quantify the number of individual water molecules used in the experiment, a key concept for understanding chemical reactions in biological systems.
A sample contains 3.01 × 10^23 molecules of carbon dioxide (CO2). Determine the number of moles in the sample and calculate the number of oxygen atoms present. Explain your reasoning.
To find moles, divide the number of molecules by Avogadro’s number: 3.01 × 10^23 ÷ 6.022 × 10^23 = 0.50 moles of CO2. Each molecule of CO2 contains two oxygen atoms, so multiply the number of molecules by 2 to get the number of oxygen atoms: 3.01 × 10^23 × 2 = 6.02 × 10^23 atoms of oxygen. This demonstrates how understanding molar relationships and molecular composition helps biologists determine atomic quantities involved in physiological and environmental processes, such as carbon cycling and respiration.

