AP Syllabus focus:
‘A thorough discussion on extrapolation, including its definition and the risks associated with predicting a response value using a value of the explanatory variable outside the interval of x-values used to create the regression line. It will emphasize the unreliability of extrapolated estimates, especially as the distance from the known data range increases, highlighting the practical implications of extrapolation in data analysis.’
Extrapolation is a critical idea in regression analysis, reminding us that predictions made beyond observed data can be misleading, unstable, and often statistically unreliable.
Understanding Extrapolation in Regression Analysis
Extrapolation arises when a regression model is used to predict a response variable based on an explanatory variable that lies outside the range of observed data used to construct the model.
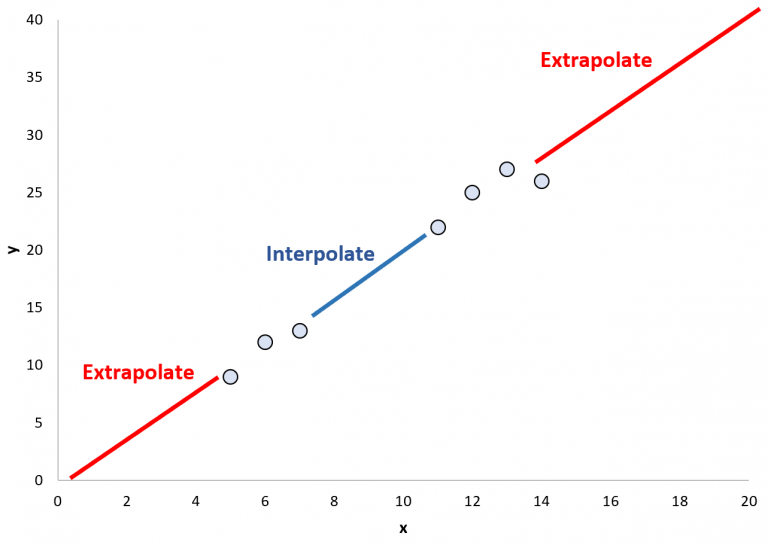
This plot highlights the distinction between interpolation within the data range and extrapolation beyond it, reinforcing that the regression line is only supported by observed values. Source.
Regression equations, including the least-squares regression line, are built entirely on the relationships contained within the sample. When predictions extend beyond this domain, the underlying model may no longer describe the true association between the variables.
Extrapolation: The use of a regression model to predict a response value for an explanatory variable that lies outside the interval of observed x-values.
Regression equations, including the least-squares regression line, are built entirely on the relationships contained within the sample. When predictions extend beyond this domain, the underlying model may no longer describe the true association between the variables.
Why Extrapolation Is Risky
The AP Statistics curriculum emphasizes that extrapolated predictions are unreliable because they lack empirical support. When the explanatory variable moves beyond the scope of the original data, the regression line may extend into regions where:
the form of the relationship may change,
the strength of the relationship may weaken or strengthen, or
external factors may alter the association entirely.
Even a model with a strong correlation or a high coefficient of determination within the data range cannot guarantee meaningful predictions outside that range.
How Extrapolation Differs from Interpolation
Interpolation involves predicting a response value for an explanatory value within the data’s observed interval. Because empirical patterns exist inside the interval, these predictions are far more defensible. Extrapolation, however, pushes the model into an unknown region.
Interpolation: Predicting a response value for an explanatory variable that lies within the interval of observed x-values.
Predictions generated by extrapolation can deviate sharply from actual behaviors, even when the observed relationship appears linear and stable.
Identifying Extrapolation in Practice
When evaluating whether a prediction counts as extrapolation, students should examine the domain of observed x-values.
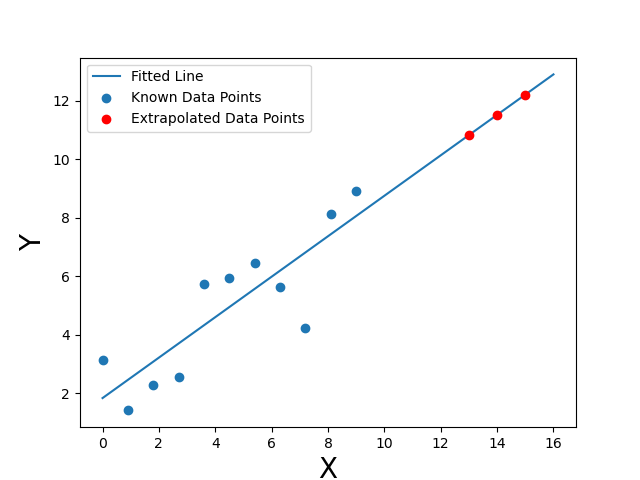
The graph contrasts known data with extrapolated predictions extending along the same fitted line, emphasizing how extrapolated values fall beyond the supported x-range of the model. Source.
To determine this:
Identify the minimum and maximum x-values in the dataset.
Compare the proposed x-value for prediction with this interval.
If the x-value falls outside the boundaries, the prediction is extrapolated.
Because models are sensitive to context, any values even slightly beyond the observed range should be treated cautiously.
Why Extrapolation Becomes More Unreliable as Distance Increases
The syllabus stresses that the farther the extrapolated x-value is from the sample data, the more unreliable the prediction becomes.
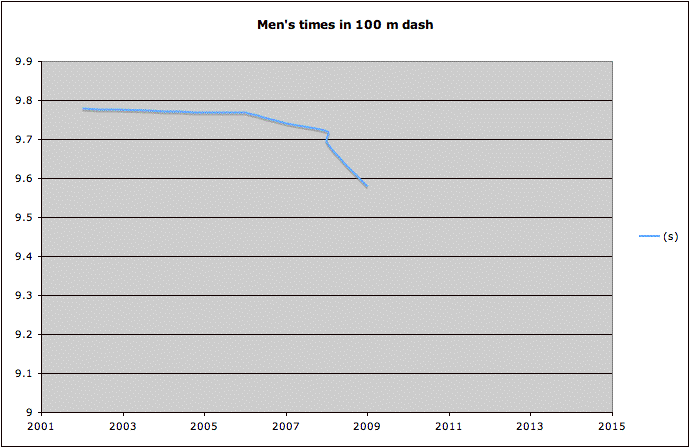
This plot demonstrates how extending a trend far beyond observed years can imply unrealistic performance improvements, illustrating the growing inaccuracy of predictions made at increasing distances from the data. Source.
This happens because:
regression lines assume the relationship remains unchanged,
real-world relationships often curve, level off, or reverse beyond the observed range, and
sampling conditions may not reflect broader or extreme values.
These issues accumulate with increasing distance, making long-range predictions particularly problematic.
Theoretical Basis for Avoiding Extrapolation
Regression models summarize patterns in the sample, not the population across all possible values. For linear regression, the model is defined by:
EQUATION
= Predicted response value
= Explanatory variable value
= Estimated y\text{-}intercept
= Estimated slope
Although this equation extends infinitely in both directions mathematically, its statistical credibility does not. The model parameters are optimized only for the observed interval, making predictions beyond that range speculative.
A key idea for AP students is that statistical models are context dependent, and extrapolation ignores this dependence. Real-world variables rarely behave linearly across all possible ranges, and sharp deviations can occur without warning.
Practical Implications for Data Analysis
Understanding the dangers of extrapolation helps prevent overinterpretation of regression results. When predictions are attempted far from the observed interval:
values may be biologically, physically, or logically impossible,
predicted trends may contradict known behavior of the system, and
the confidence in the prediction becomes extremely low.
Students must be prepared to recognize when a prediction request is outside the meaningful range of the model.
Evaluating Predictions in Applied Settings
Whenever a prediction is made, students should incorporate the following checks:
Assess the data range: Compare the input x-value to the observed interval.
Consider contextual realism: Reflect on whether the relationship is likely to hold beyond observed data.
Flag predictions with uncertainty: Clearly identify extrapolated predictions as speculative.
These practices support clearer communication and prevent misinterpretations when reporting regression-based conclusions.
FAQ
In real-world data, variables are often affected by unmeasured factors that may change beyond the observed range, making trends less stable outside the sample.
Controlled experiments restrict external influences, so relationships tend to behave more predictably within and slightly beyond the tested range.
However, observational data rarely offer such stability, meaning extrapolated predictions can deviate sharply from reality.
A scatterplot allows you to visually inspect the minimum and maximum observed x-values.
If the predicted x-value lies clearly to the left or right of all plotted data points, the prediction is an extrapolation.
This visual approach is especially helpful when the data range is not explicitly stated in the problem.
A strong correlation only indicates a stable linear pattern within the observed data. It does not guarantee that the same pattern continues beyond the sample.
Strong internal correlation can even give a false sense of reliability, encouraging overconfidence in predictions that remain unsupported outside the data range.
Clues include:
• biological or physical limits that cap possible values
• evidence of curvature near the boundaries of the data
• contextual knowledge suggesting diminishing or changing effects
Any indication that the relationship is unlikely to remain linear should raise caution about extrapolation.
Extrapolation may be acceptable when:
• no relevant data exist beyond the range
• short extensions beyond the data are supported by strong contextual reasoning
• the costs of inaction outweigh the uncertainty of prediction
Even in such cases, the limitations and uncertainty of extrapolated values must be clearly communicated.
Practice Questions
Question 1 (1–3 marks)
A researcher records data on the number of hours students spend studying each week (x) and their test scores (y). The observed values of x range from 2 to 15 hours. The researcher uses the regression line to predict a test score for a student who reports studying 30 hours in a week.
a) Explain why this prediction may be unreliable.
(2 marks)
Question 1 (2 marks)
a) Award 1 mark for identifying that the x-value (30 hours) lies outside the observed range of data (2–15 hours).
Award 1 mark for stating that predictions made outside the data range are unreliable because the relationship may not remain the same beyond the observed values.
Question 2 (4–6 marks)
A biologist investigates the relationship between the age of a species of tree (x, in years) and its height (y, in metres). A linear regression model is fitted using data from trees aged 5 to 40 years.
a) Define extrapolation in the context of this study.
b) The biologist uses the model to predict the height of a 100-year-old tree. Give two reasons why this prediction may be inappropriate.
c) Suggest one action the biologist could take to obtain a more reliable estimate for older trees.
(5 marks)
Question 2 (5 marks)
a) Award 1 mark for a correct definition: extrapolation is using the model to predict a value when the x-value lies outside the range of data used to create the regression line.
b) Award 1 mark for explaining that 100 years is far outside the observed age range (5–40 years).
Award 1 mark for noting that the relationship between tree age and height may change beyond the observed data (for example, the tree’s growth may slow or stop).
c) Award 1 mark for suggesting collecting data from older trees.
Award 1 mark for an additional suitable suggestion such as using a model better suited to long-term growth, consulting biological knowledge, or fitting a non-linear model.

