This section explains how p-values guide formal statistical decisions, emphasizing the role of the significance level (α) and how evidence from data determines whether to reject the null hypothesis.

Decision Making with p-Values

Statistical decision-making uses the relationship between the p-value and the significance level (α) to determine whether evidence from the sample is strong enough to reject the null hypothesis (H₀). Because the p-value quantifies the probability of observing data as extreme as what was collected if H₀ is true, it serves as a direct measure of the strength of evidence against H₀.

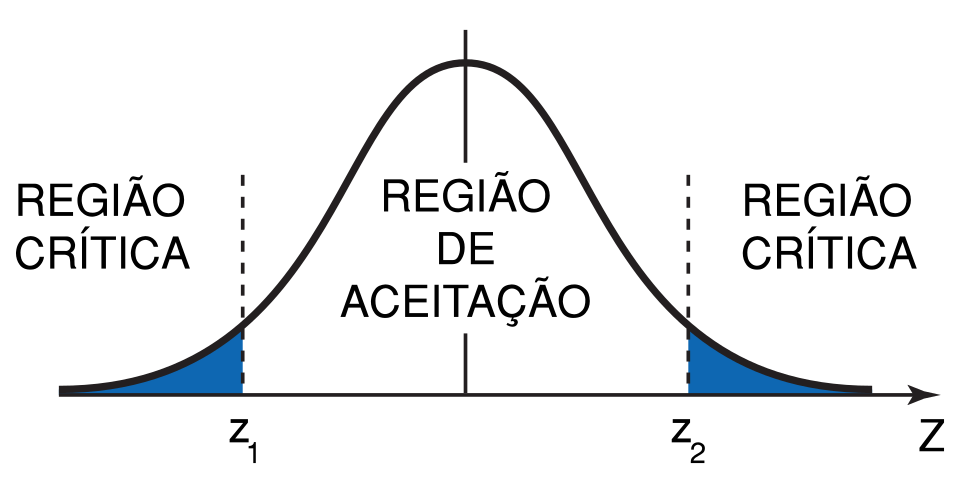
A normal distribution with a shaded critical region highlights how unlikely outcomes under the null model correspond to small p-values. The shaded area represents α, the threshold for rejecting the null hypothesis. Source.

Understanding the Role of the Significance Level

The significance level (α) is a researcher-selected threshold that defines how unlikely the sample results must be, under H₀, before rejecting the null hypothesis. Common choices such as α = 0.05 or α = 0.01 reflect tolerance for the risk of mistakenly rejecting a true null hypothesis. A smaller α indicates a more conservative stance on rejecting H₀, requiring stronger evidence.

Statistical decisions rely on comparing these two values, where the p-value is interpreted relative to α rather than in isolation.

Comparing p-Values to α

The decision process depends directly on whether the p-value is less than, equal to, or greater than α. This comparison determines whether the observed data align with what would typically occur if H₀ were true.

• If p-value ≤ α: Reject H₀ because the data are sufficiently unlikely under the null model.

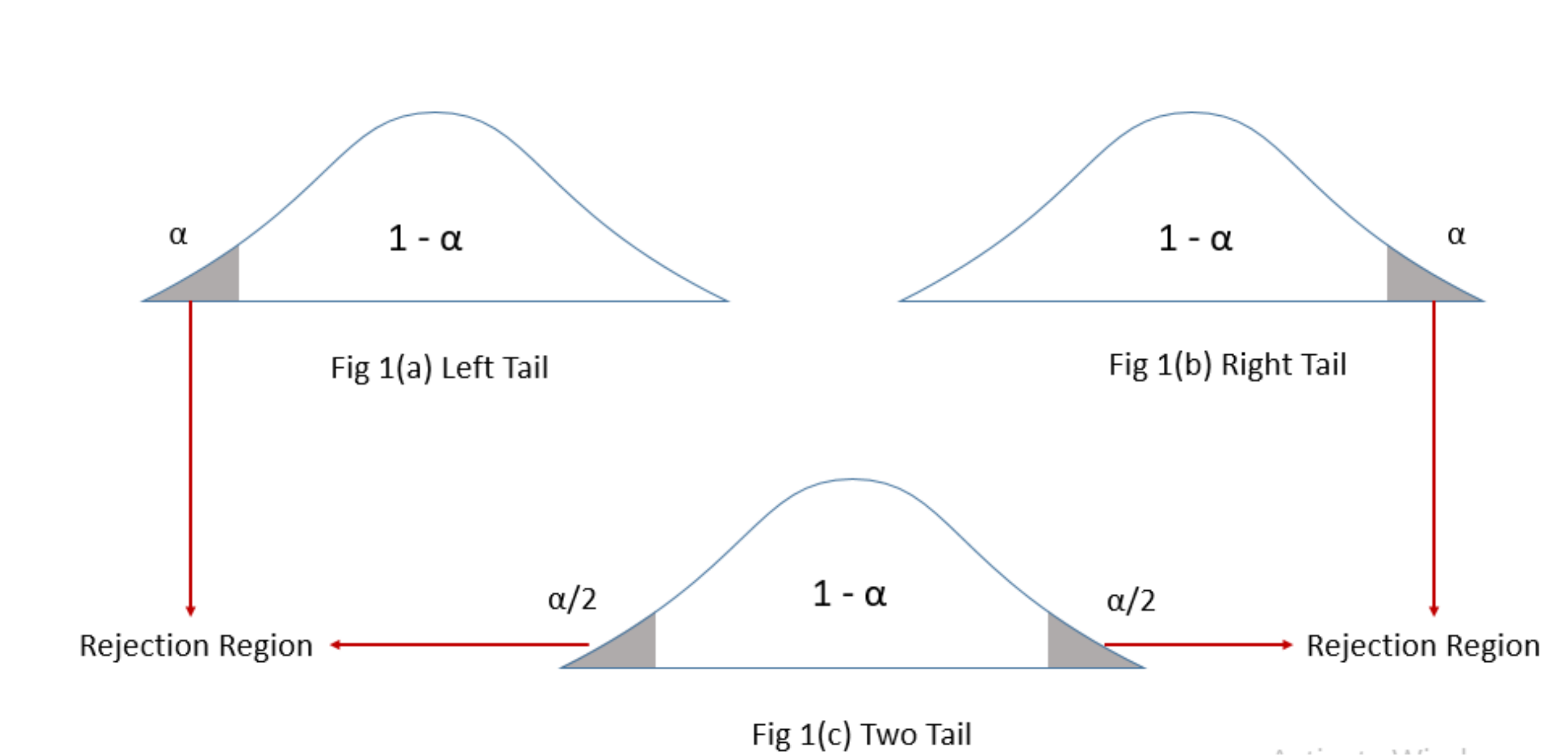
Rejection-region diagrams for left-, right-, and two-tailed tests illustrate how α determines which outcomes lead to rejecting H0H_0H0​. Each shaded region corresponds to values that would yield p-values at or below α. Source.

• If p-value > α: Fail to reject H₀ because the data are not unlikely enough to claim evidence against it.

Because hypothesis tests do not prove hypotheses, a failure to reject H₀ does not confirm it; instead, it indicates insufficient statistical evidence.

Interpreting Decision Outcomes

The interpretation of decisions must always remain rooted in the study’s context. Rejecting H₀ suggests that the alternative hypothesis (Hₐ) is better supported by the sample data. Failing to reject H₀ indicates that the evidence does not meet the required strength set by α. The p-value communicates degree of support, not certainty.

One sentence of normal text is required here before providing an equation block, ensuring conceptual continuity.

Linking p-Values to Statistical Evidence

Lower p-values provide stronger evidence against H₀ because they indicate that the observed data would rarely occur if the null hypothesis were true. The interpretation is not absolute; instead, it reflects how well the data align with the null model.

EQUATION

Researchers must therefore ensure the significance level is chosen before data collection. Selecting α post-analysis biases decisions and invalidates the statistical reasoning that underlies hypothesis testing.

Decision-Making Framework

Students should internalize the structured reasoning used in significance testing. The framework ensures consistency and transparency in how claims are supported by the statistical evidence provided by the p-value.

Follow this logical process:

• Identify the research question and define H₀ and Hₐ clearly.

• Select α in advance based on the context and acceptable risk level.

• Compute the test statistic and resulting p-value using appropriate formulas.

• Compare the p-value to α during the decision step.

• Interpret the outcome in context, emphasizing evidence—not proof.

The decision based on the p-value ultimately determines how strongly the data contradict the null hypothesis. When the p-value falls below α, the data are regarded as sufficiently incompatible with H₀ to justify rejection. When it does not, the evidence is deemed too weak to support the alternative.

Using Context to Support Decisions

Hypothesis testing never occurs in isolation from real-world meaning. The significance level should reflect the consequences of errors, while the interpretation of the decision must explicitly connect back to the population and proportion under investigation. Clear communication of the reasoning—especially how the p-value supports or fails to support a claim—ensures that statistical conclusions are meaningful, responsible, and aligned with the AP Statistics curriculum.