Random variation occurs naturally in data and can cause statistical conclusions to differ from reality. Understanding how this randomness leads to inference errors is essential for sound decision-making.

Understanding Random Variation in Statistical Inference

Random variation refers to the unpredictable fluctuations that occur when data are collected from a population. Because every sample differs, statistical estimates vary, which makes inference inherently uncertain. Recognizing how this uncertainty produces mistakes in hypothesis testing is central to evaluating the reliability of conclusions.

When random variation affects sample outcomes, it can mislead analysts into thinking an effect exists when it does not, or missing an effect that truly exists. These possibilities form the basis of formal inferential error types, each carrying different consequences for interpretation. Considering the probabilities of these errors is critical whenever conclusions are drawn from sample data rather than full population information.

Sampling Variability and Its Role in Error

Sampling variability describes how sample statistics differ from sample to sample.

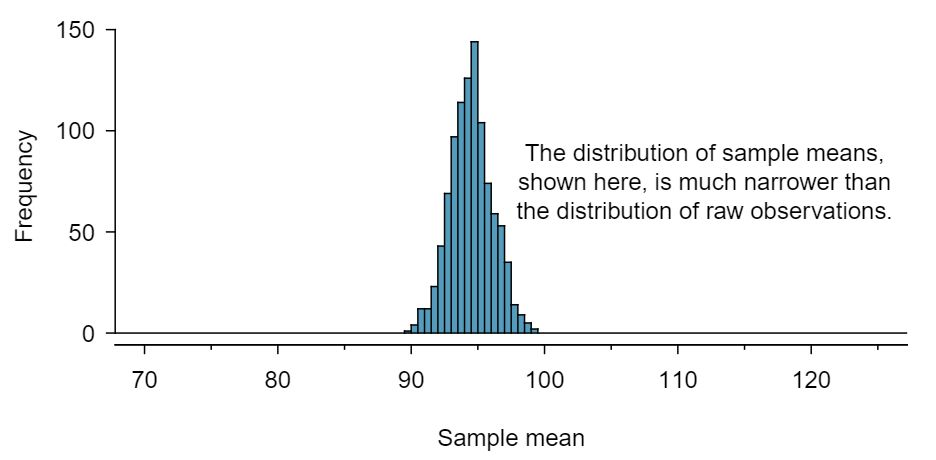
Histogram illustrating sampling variability across repeated samples; the spread of sample means shows how randomness contributes to uncertainty in inference. Source.

It is a fundamental reason why errors occur in inference because statistical procedures rely on sample evidence to estimate unknown parameters. Even under perfect data collection, two samples of equal size from the same population are unlikely to produce identical results.

Researchers must therefore evaluate the strength of evidence provided by the sample while acknowledging that randomness may distort the observed results. This awareness is especially important when interpreting borderline outcomes from hypothesis tests.

Types of Errors in Statistical Inference

Hypothesis tests involve decisions based on sample evidence, and random variation creates two distinct error possibilities.

A Type I error is often described as a “false positive.” Its probability, denoted α, is chosen by the researcher as the significance level. This probability reflects the long-run frequency with which a correct null hypothesis would be rejected under repeated sampling.

A different mistake arises when the test fails to detect an actual effect.

The probability of a Type II error is denoted β, and it depends on factors such as sample size, effect size, and inherent variability.

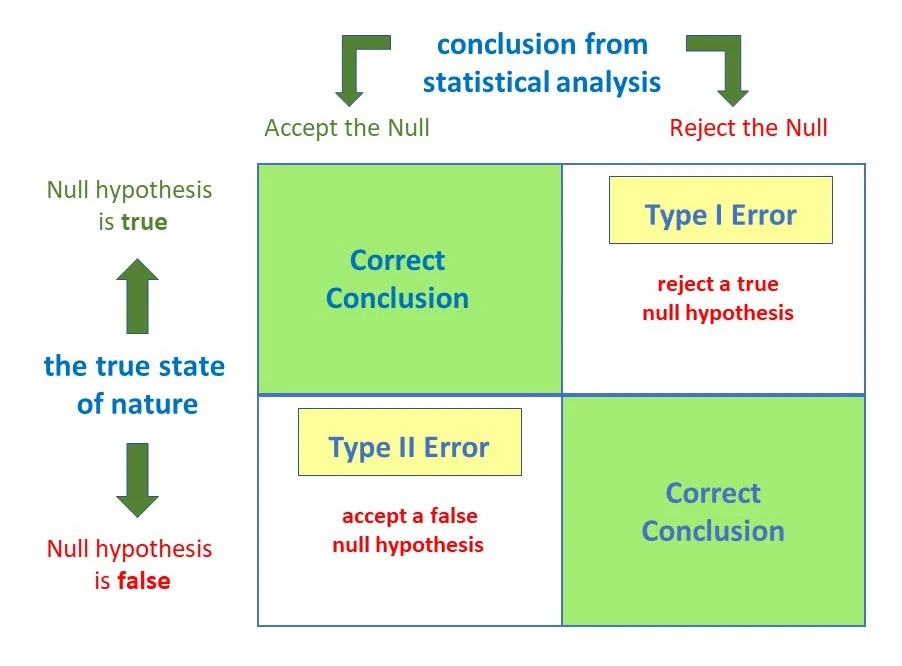
Matrix showing the four possible outcomes of hypothesis testing, clearly distinguishing correct decisions from Type I and Type II errors. Source.

These two errors move in opposite directions; reducing the chance of one typically increases the chance of the other.

Probabilities of Error and Their Interpretation

Understanding the probabilities of Type I and Type II errors enables researchers to evaluate the risks associated with inferential decisions. Because α is set before data collection, it provides a clear threshold for assessing evidence. A smaller α reduces the chance of falsely declaring a significant result but makes it harder to detect real differences. Meanwhile, β is rarely predetermined, yet its complement—power, defined as $1 - β$—represents the probability of correctly rejecting a false null hypothesis.

Although students are not required to compute β or power for basic AP Statistics work, the conceptual link between these probabilities and error risk is essential. Recognizing that any test outcome involves uncertainty helps prevent overconfident interpretations of significance results.

Implications of Inferential Errors

Inferential errors have meaningful consequences depending on the context. A Type I error may lead to adopting an ineffective policy, approving a faulty product, or reaching an incorrect scientific conclusion. A Type II error may allow real problems to go undetected or lead researchers to overlook important relationships. Because the impact of each error type differs across scenarios, analysts must evaluate which mistake carries greater cost and adjust significance levels or study design accordingly.

Bullet-point considerations illustrate why thoughtful interpretation is vital:

• Type I errors risk acting on results driven by random variation rather than true effects.

• Type II errors risk inaction when real differences or relationships exist.

• Choosing α involves balancing caution against sensitivity.

• Understanding β helps frame the limitations of the evidence.

Importance of Accounting for Random Variation

Recognizing that sample outcomes vary is crucial when making conclusions from statistical analyses. Even when correct procedures are followed, randomness may lead to sample results that misrepresent the underlying population. Therefore, researchers must:

• Evaluate the strength of the evidence relative to potential error risks.

• Avoid overstating certainty, especially near decision thresholds.

• Consider study design choices—such as sample size—to reduce the likelihood of errors.

By integrating awareness of random variation and its consequences, analysts can produce more reliable and responsible interpretations grounded in statistical reasoning.