This section explains how to justify a claim after a significance test for two population proportions by connecting statistical decisions to real-world research questions.

Understanding the Role of Claims in Significance Testing

Justifying a claim after conducting a significance test for the difference of two population proportions requires interpreting the statistical decision in the context of the research question. The goal is to move beyond numerical results and explain what the decision about the null hypothesis means for the populations being studied. Because claims influence conclusions drawn from data, it is essential to clearly connect the test’s outcome to the practical situation motivating the study.

Linking Test Decisions to Claims

A statistical test yields either a rejection or a failure to reject the null hypothesis, and each outcome guides how claims should be supported. The null hypothesis represents no difference between the population proportions, while the alternative hypothesis represents the claim being tested. When presenting results, students must articulate how the statistical evidence aligns with or fails to support the investigated claim.

Evidence From the p-Value

The p-value serves as a central piece of information when defending a claim. It quantifies the likelihood of observing the sample difference or something more extreme if the null hypothesis were true.

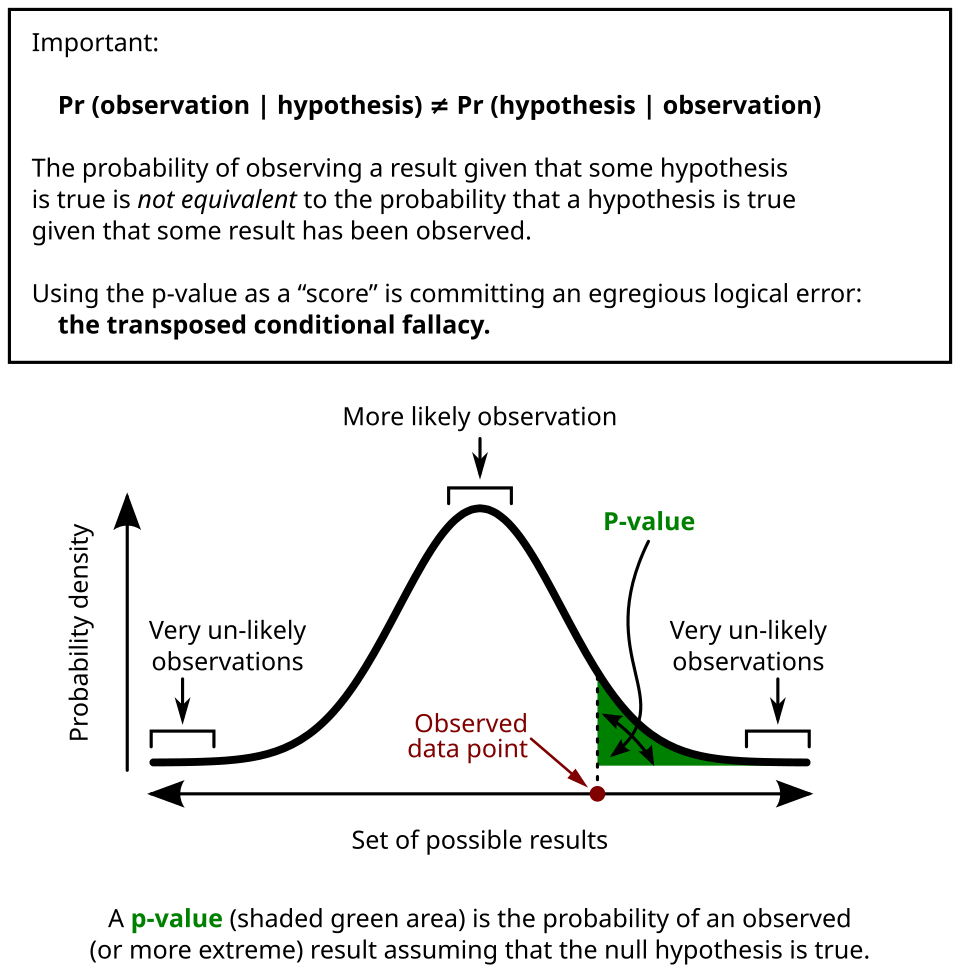
This diagram illustrates the p-value as the shaded tail area under the distribution assuming the null hypothesis is true, highlighting how extreme the observed statistic is relative to that distribution. Source.

When using the p-value to justify a claim, students must discuss whether the evidence is statistically convincing at the chosen significance level, which determines the threshold for rejecting the null hypothesis.

Connecting Statistical Results to Context

A valid justification always incorporates context from the study. The statistical decision alone is insufficient; the reasoning must reference the populations represented by the sample data. When determining whether the test results support a claim, it is crucial to specify the direction and nature of the difference implied by the alternative hypothesis and relate it back to the subject matter of the research question. Without contextual interpretation, the claim lacks meaningful grounding.

Structuring a Claim Justification

A high-quality justification integrates statistical reasoning and contextual interpretation in a logical manner. Students should present information clearly and support claims systematically.

Essential Components of a Claim Justification

• Restatement of the research question to anchor the interpretation.

• Identification of the statistical decision, noting whether the null hypothesis is rejected or not.

• Discussion of the p-value and how it compares to the significance level.

• Explanation of what the decision means for the populations, stated in clear, contextual language.

• Articulation of whether the statistical evidence supports the claim, avoiding overstatements about proving the hypothesis.

A justification must avoid implying certainty. Significance testing provides evidence, not proof, and claims must reflect this probabilistic nature.

Statistical Logic Behind Supporting a Claim

When the test leads to rejection of the null hypothesis, the sample data are considered inconsistent with no difference between the population proportions.

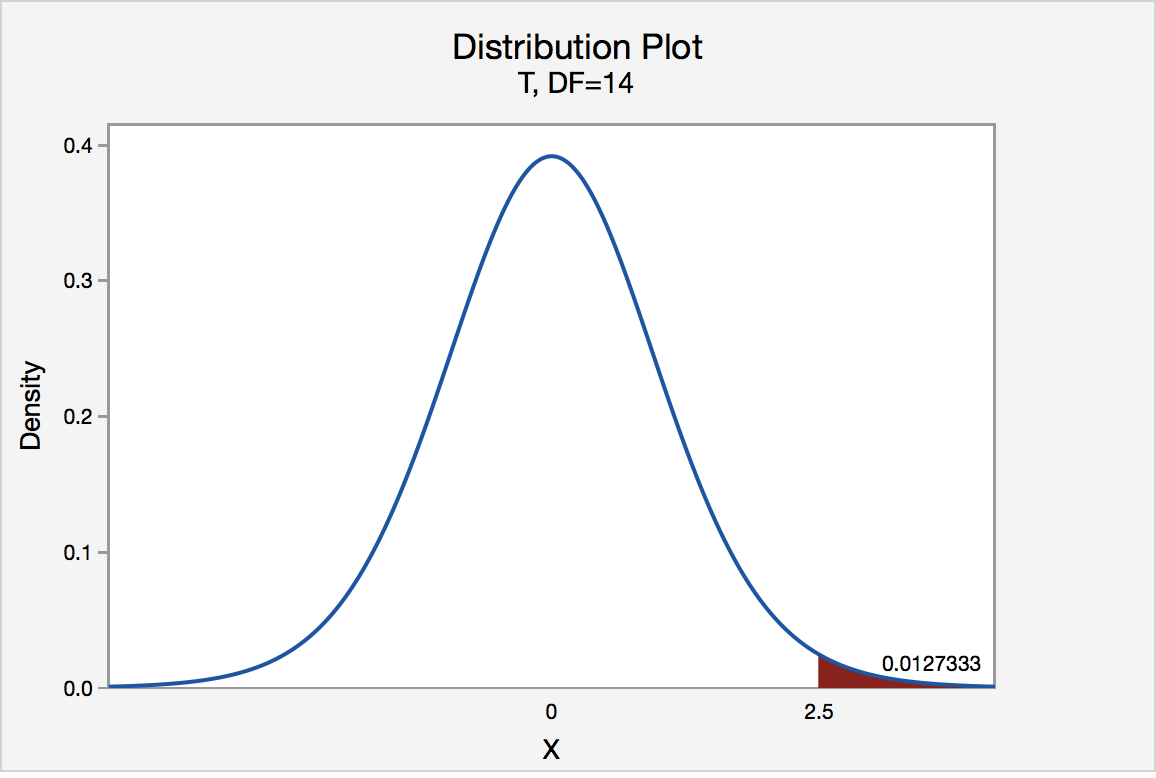
This plot shows a right-tailed test where the shaded region represents the p-value, demonstrating how tail probability is used to evaluate evidence against the null hypothesis. Although the example uses a t-distribution, the same principle applies to z-tests for proportions. Source.

This inconsistency provides statistical evidence in favor of the alternative hypothesis. Therefore, a claim aligned with the alternative hypothesis can be supported by stating that the observed difference is unlikely to be due to random sampling variation alone at the chosen significance level.

When the test fails to reject the null hypothesis, the justification changes. The evidence is not strong enough to conclude that the population proportions differ. However, this outcome does not validate the null hypothesis; instead, it indicates a lack of convincing evidence for the claim represented by the alternative hypothesis.

Interpreting the Implications for Populations

A strong justification highlights what the statistical findings imply about the underlying populations. Because the test is built on sample data, students must clearly distinguish between sample outcomes and population inferences. Claims should be expressed in terms such as “there is evidence that” or “there is not sufficient evidence to conclude,” which convey the tentative, evidence-based nature of statistical reasoning.

Avoiding Misinterpretations When Justifying Claims

Several common pitfalls can weaken a justification. Students must avoid equating a large p-value with proof that the population proportions are equal or implying that rejection guarantees the alternative hypothesis is true. Additionally, justifications should not describe the p-value as the probability that the null hypothesis is correct. Instead, explanations must focus on what the p-value indicates about the plausibility of the observed sample results under the assumption of the null hypothesis.

Key Practices for Effective Claim Support

• Use precise statistical language that reflects uncertainty appropriately.

• Refer explicitly to population proportions, not just sample values.

• Connect each statistical step back to the research context and the stated claim.

• Present reasoning that is logically consistent with the test results and the structure of hypothesis testing.

By centering the interpretation on context, statistical evidence, and sound reasoning, students can convincingly justify claims based on the results of a significance test for the difference between two population proportions.