OCR Specification focus:
‘For charged particles, energy gained eV equals kinetic energy increase ½ m v².’
When charged particles accelerate through a potential difference, they gain kinetic energy equal to the electrical energy transferred. This relationship underpins particle motion in electric fields.
Electron Energy Gain: eV = ½mv²
Charged particles such as electrons and ions experience a force when they move through an electric potential difference (p.d.). This causes them to accelerate, converting electrical energy into kinetic energy. The relationship between the energy gained and the resulting velocity of the particle is fundamental to understanding electric fields, particle beams, and components such as cathode ray tubes.
The Nature of Energy Transfer in an Electric Field
When a charge (Q) moves through a potential difference (V), it experiences an energy transfer (W) equal to the product of charge and potential difference. This is the basis of the energy equation W = VQ. For a single charged particle, the same concept applies but is typically expressed in terms of elementary charge (e) and electron energy gain.
As a charged particle accelerates through a uniform electric field, its electrical potential energy decreases, and its kinetic energy increases by the same amount (assuming negligible losses).
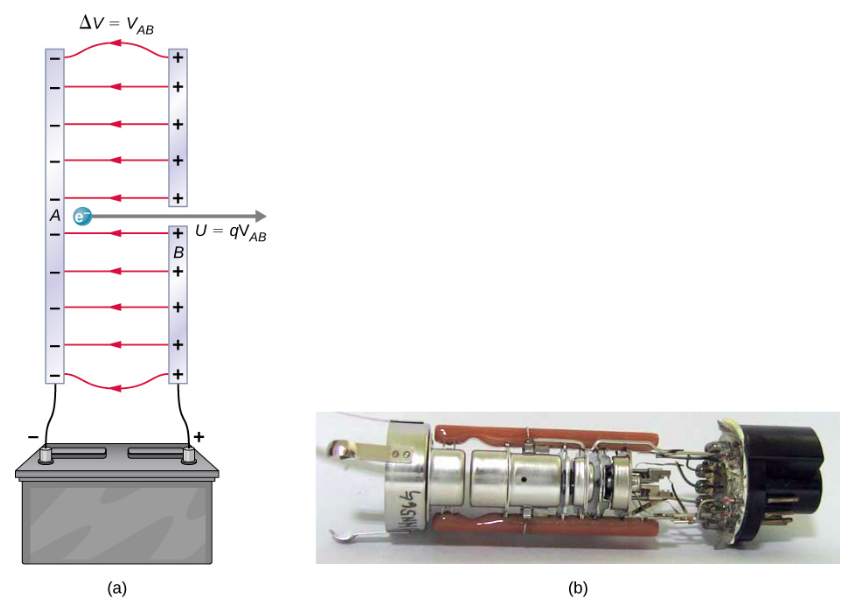
Electron accelerated between parallel plates by a potential difference VABV_{AB}VAB. By conservation of energy, the electron’s kinetic energy increase equals the electrical work: KE=qVKE = qVKE=qV. This illustrates the physical basis of the relation eV=12mv2eV = \tfrac{1}{2}mv^2eV=21mv2. Source.
Defining the Electronvolt
Electronvolt (eV): The electronvolt is the amount of energy gained (or lost) by a single electron when it moves through a potential difference of 1 volt.
This unit provides a convenient measure for small energy changes typical in atomic and subatomic physics. One electronvolt is equal to 1.6 × 10⁻¹⁹ joules, reflecting the charge of an electron multiplied by one volt.
A particle with greater charge, such as a doubly ionised helium ion (He²⁺), gains twice the energy when accelerated through the same potential difference because energy gained is proportional to charge.
Linking Electrical and Kinetic Energy
The energy gained by a charged particle moving through a potential difference is expressed using the key relationship for this subsubtopic:
EQUATION
—-----------------------------------------------------------------
Electron Energy Gain (eV) = ½ m v²
e = charge of the electron (1.6 × 10⁻¹⁹ C)
V = potential difference (V)
m = mass of the particle (kg)
v = velocity after acceleration (m s⁻¹)
—-----------------------------------------------------------------
This equation shows that the kinetic energy acquired by a charged particle after being accelerated from rest through a potential difference equals the electrical energy transferred to it.
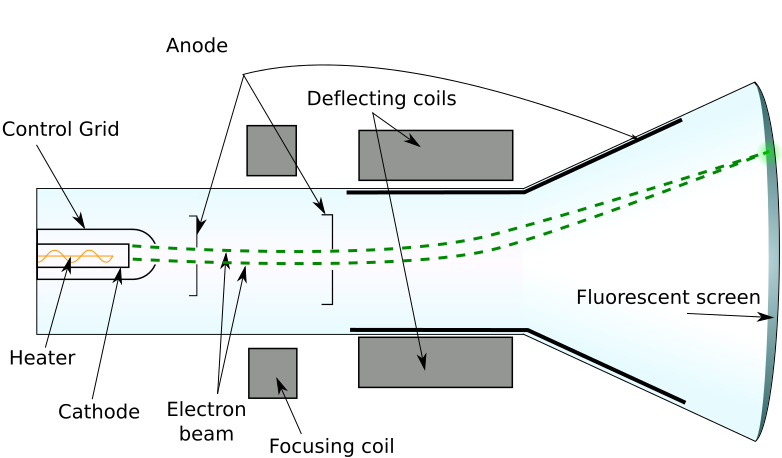
Cutaway diagram of a cathode-ray tube showing the electron gun, accelerating anodes, and phosphor screen. Electrons gain kinetic energy from the anode potential and then are focused and deflected before striking the screen. Extra labels beyond the syllabus (e.g., focusing/deflection elements) are included for orientation only. Source.
Between the points where it starts and stops accelerating, all of the work done by the electric field becomes kinetic energy, provided there are no other energy losses such as collisions or radiation.
Deriving the Relationship
To understand the derivation, recall that work done (W) on a charge moving through a potential difference is:
EQUATION
—-----------------------------------------------------------------
Work Done (W) = Charge × Potential Difference
W = QV
—-----------------------------------------------------------------
For a single electron, Q = e, so the work done becomes W = eV. If this work entirely converts to kinetic energy, then eV = ½mv². This forms the foundation for measuring or calculating the speed of electrons in electric fields.
This expression also implies that the velocity of the particle depends on both its mass and the accelerating voltage. Smaller mass and higher potential difference lead to greater speeds.
Conceptual Understanding of eV = ½mv²
Electrical Energy Input (eV): Energy supplied by the field due to the potential difference.
Kinetic Energy Output (½mv²): Energy gained by the particle as motion.
Energy Conservation: No net loss; electrical energy is converted to kinetic form.
This process is a key example of energy conversion within physics — transforming potential energy into kinetic energy. The direction of motion is along the electric field lines for positive charges, and opposite for negative charges.
The Importance of Charge Sign and Direction
Although energy gained (eV) is always positive, the force direction and motion depend on the sign of the charge. For example:
A positive charge accelerates towards lower potential (in the direction of the field).
A negative charge (like an electron) accelerates towards higher potential (against the field).
This distinction is crucial for interpreting circuit behaviour and designing experiments such as electron beam deflection or photoelectron emission studies.
Applications and Physical Contexts
The relationship eV = ½mv² is foundational in many areas of physics and technology:
Cathode Ray Tubes (CRTs): Electrons are accelerated by a known potential difference, and their velocity determines the beam’s position on a screen.
Electron Guns and Accelerators: The kinetic energy of emitted electrons is precisely controlled by the accelerating voltage.
Photoelectric Effect: The maximum kinetic energy of emitted electrons equals the photon energy minus the work function, often expressed in electronvolts.
Mass Spectrometry: Ion velocities, determined using this equation, allow mass-to-charge ratios to be calculated.
In all these applications, measuring eV allows conversion between energy gained in electrical systems and motion characteristics of particles.
Relating eV to the Joule
Conversion Factor: 1 eV = 1.6 × 10⁻¹⁹ J.
This conversion is essential for using electronvolt-based energies in SI unit calculations. While eV is convenient for atomic scales, joules remain the standard for larger-scale energy measurements.
The small magnitude of the electronvolt makes it suitable for atomic, molecular, and nuclear physics, where energy changes typically fall in this range.
Experimental Determination of Electron Velocity
The speed of an electron after acceleration can be calculated directly using eV = ½mv², rearranged as:
EQUATION
—-----------------------------------------------------------------
Velocity (v) = √(2eV / m)
—-----------------------------------------------------------------
This expression shows that velocity increases with the square root of the potential difference and decreases with particle mass. For electrons, even small potential differences can result in high speeds due to their very low mass.
Limitations and Assumptions
This equation assumes:
The particle starts from rest.
All energy gained is converted to kinetic energy.
There are no collisions or radiation losses.
In real systems, some energy may be lost, but for vacuum acceleration or low-pressure conditions, the approximation holds very well.
Summary of Conceptual Flow
Electric potential difference provides an energy gradient.
Charged particles experience force and acceleration.
Electrical energy converts to kinetic energy.
The total energy gained depends on charge magnitude and potential difference.
eV = ½mv² quantifies this direct conversion of energy.
Through this relationship, the link between electric fields, charge motion, and kinetic energy becomes mathematically and physically clear — a cornerstone of A-Level Physics understanding of particle acceleration.
FAQ
The electronvolt (eV) is a much smaller unit than the joule and is more practical for describing the tiny energy changes of individual particles such as electrons or ions.
1 eV = 1.6 × 10⁻¹⁹ J, so it keeps numbers manageable and avoids the use of very small decimals.
Physicists and engineers use electronvolts when dealing with atomic, nuclear, or particle-level energies, where typical values range from a few eV to several MeV (million electronvolts).
An electron is negatively charged, so it accelerates towards the positive electrode (higher potential) and opposite to the direction of the electric field lines.
The electric field exerts a constant force on the electron as long as the field remains uniform. Once the electron leaves the region of the field, it continues moving at constant velocity unless acted upon by another force.
At very high accelerating voltages, an electron’s velocity approaches a significant fraction of the speed of light, and relativistic effects become important.
In such cases, kinetic energy no longer equals ½mv², because mass effectively increases with speed.
Physicists then use the relativistic energy equation that accounts for changes in mass and time dilation, which ensures accurate energy predictions at relativistic speeds.
Yes. The relationship applies to any charged particle, positive or negative, provided the charge value is used correctly.
For ions:
Replace e with the actual charge q of the ion (for example, 2e for a doubly ionised helium ion).
The same principle holds: the electrical energy gained equals the kinetic energy increase.
Heavier ions, however, gain much less velocity than electrons for the same voltage because of their far greater mass.
Several laboratory and industrial setups use this principle to determine electron energy:
Electron diffraction experiments, where the wavelength of accelerated electrons reveals their kinetic energy.
Photoelectric emission setups, where stopping potential measurements show how much energy electrons possess.
Cathode ray tubes, where deflection on a fluorescent screen indicates the electron’s speed and energy.
Each method uses measurable effects—deflection, wavelength, or stopping voltage—to indirectly confirm the relationship between potential difference and kinetic energy gain.
Practice Questions
Question 1 (2 marks)
An electron is accelerated from rest through a potential difference of 200 V.
(a) State the energy gained by the electron in electronvolts.
(b) Explain briefly what this value represents in terms of the electron’s motion.
Mark Scheme
(a) 200 eV or correctly stated equivalent value in eV (1 mark)
(b) Energy gained per electron equals the work done by the electric field; it becomes the electron’s kinetic energy after acceleration (1 mark)
Question 2 (5 marks)
An electron starts from rest and is accelerated through a potential difference of 5000 V.
(a) Derive an expression linking the electron’s speed to the accelerating potential difference and its charge and mass.
(b) Calculate the speed of the electron after acceleration.
(c) State one assumption made in this calculation and explain why it is reasonable.
Mark Scheme
(a) Use energy conservation: electrical energy = kinetic energy (1 mark)
eV = ½mv² (1 mark)
Rearranged to give v = √(2eV / m) (1 mark)(b) Substitution using e = 1.6 × 10⁻¹⁹ C, m = 9.11 × 10⁻³¹ kg, V = 5000 V → v ≈ 4.2 × 10⁷ m s⁻¹ (1 mark)
(c) Assumes no energy losses (e.g. due to collisions or radiation); reasonable in a vacuum or low-pressure tube (1 mark)

