OCR Specification focus:
‘Energy transferred by a device: W = V I t.’
Electrical devices transfer energy whenever current flows through them. Understanding how energy transfer relates to potential difference, current, and time is essential for analysing circuit performance and calculating energy efficiency in practical applications.
The Concept of Energy Transfer in Electrical Circuits
When an electrical device operates, it converts electrical energy supplied by a source into other forms such as light, heat, sound, or mechanical energy. The rate and amount of this energy transfer depend on the potential difference (V) across the device, the current (I) flowing through it, and the time (t) for which it operates.
The total energy transferred provides a quantitative measure of how much work an electrical component performs. This relationship allows physicists and engineers to determine both efficiency and cost in domestic and industrial energy usage.
Understanding the Relationship Between Voltage, Current, and Energy
The potential difference across a component represents the energy transferred per unit charge as electric charge moves through it. When current flows, a continuous movement of charge occurs, leading to a steady energy transfer over time.
Each coulomb of charge carries an energy amount equal to the potential difference in volts. The total energy transferred increases with both the current and the time of operation, forming the basis of the key energy transfer equation.
EQUATION
—-----------------------------------------------------------------
Energy Transfer in Circuits (W = V I t)
W = energy transferred (joules, J)
V = potential difference across the device (volts, V)
I = current through the device (amperes, A)
t = time for which the current flows (seconds, s)
—-----------------------------------------------------------------
Derivation and Physical Interpretation
The formula W = V I t can be derived from combining fundamental electrical relationships:
Current (I) is the rate of flow of electric charge, given by I = Q/t.
The energy transferred per unit charge is V, hence W = VQ.
Substituting Q = It gives W = VIt.
This equation shows that the energy transferred depends linearly on each of the three factors: voltage, current, and time. Doubling any one of these variables doubles the total energy output, assuming the others remain constant.
Energy Transfer in Practical Devices
Electrical devices are designed to transform energy from one form to another:
Filament lamps convert electrical energy to light and heat.
Electric motors convert electrical energy to kinetic energy.
Heaters and kettles transform electrical energy almost entirely into heat.
Speakers convert electrical signals into sound waves.
In each case, the equation W = V I t enables the calculation of total energy output over a period of use.
Power and Its Connection to Energy Transfer
Energy transfer over time is directly linked to electrical power, the rate at which energy is transferred.
Power: The rate of energy transfer or the rate at which work is done, measured in watts (W).
The relationship between power and energy is expressed as:
EQUATION
—-----------------------------------------------------------------
Power–Energy Relationship (P = W/t)
P = power (watts, W)
W = energy transferred (joules, J)
t = time taken (seconds, s)
—-----------------------------------------------------------------
Combining this with P = VI leads back to W = VIt, confirming that total energy is power multiplied by time. This reinforces the connection between instantaneous power output and total energy consumption.
Energy Transfer in Different Circuit Conditions
The form of the circuit influences how energy transfer behaves:
Series circuits: The same current flows through each component, but the potential difference divides across them, affecting the total energy delivered to each part.
Parallel circuits: Each branch receives the same voltage from the source, but the current divides, allowing different energy transfer rates across separate paths.
Resistive circuits: The resistance determines the current for a given voltage, influencing both power and energy transferred.
By analysing current and voltage in specific components, the total energy transfer over time can be predicted accurately.
The Role of Resistance in Energy Conversion
Whenever current flows through a resistance, electrical energy converts partly into thermal energy due to collisions between electrons and the metal lattice.
Resistance: A measure of how much a component opposes the flow of electric current, converting electrical energy into heat.
The Joule heating effect represents this conversion process, which is crucial in devices like toasters or heating elements. The energy transferred as heat in a resistor over time is given by combining Ohm’s law with the energy equation, leading to expressions such as W = I²Rt or W = V²t/R. These forms all originate from the primary equation W = VIt.
Measuring and Calculating Energy Transfer Experimentally
In laboratory or classroom investigations, energy transfer can be determined using simple measurements:
Record the potential difference (V) across the device using a voltmeter.
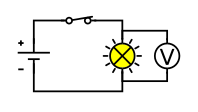
A simple circuit with a voltmeter in parallel across a component. Measuring p.d. in parallel ensures the meter reads the potential difference used in W = VIt. Clean labels and minimal elements keep the focus on correct placement of the voltmeter. Source.
Measure the current (I) using an ammeter connected in series.
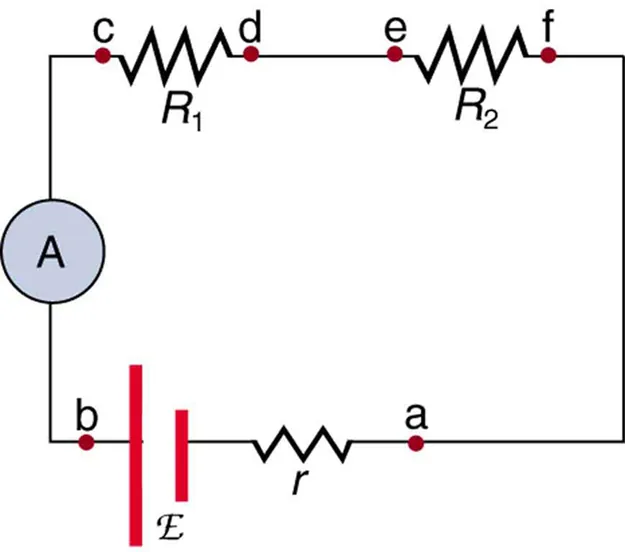
A labelled circuit diagram showing an ammeter in series with components. This layout ensures all current flows through the meter, giving the correct reading for use in W = VIt. The diagram is uncluttered and suitable for A-level learners. Source.
Measure the time (t) for which current flows using a stopwatch.
Calculate energy (W) using W = VIt.
Good experimental practice includes:
Ensuring stable voltage and current readings before timing begins.
Avoiding component overheating that might change resistance and affect accuracy.
Using data loggers for more precise time–current–voltage readings.
Applications in Energy Monitoring and Costing
The concept of energy transfer over time extends into domestic and industrial applications. Electricity meters measure the total energy transferred to a household, typically expressed in kilowatt-hours (kWh).

A close-up of a kWh electricity meter showing the register that totals energy consumed over time. This visual connects the formula W = VIt to practical metering, where energy use accumulates as appliances operate. Note: brand markings are present but not conceptually significant. Source.
Since 1 kWh equals 3.6 × 10⁶ joules, it directly relates to the same energy principles used in W = VIt.
Monitoring the energy transferred by appliances allows for:
Energy efficiency assessments—comparing how effectively devices convert electrical energy into useful forms.
Cost calculations—linking energy consumption to tariff rates.
Environmental evaluation—understanding how reducing total energy transfer contributes to lower emissions and sustainable usage.
Summary of Key Relationships
Energy transferred (W) depends on potential difference (V), current (I), and time (t).
Power (P) represents the rate of this transfer, with P = VI and W = VIt forming the foundation for electrical energy analysis.
These principles underlie practical applications in measurement, efficiency evaluation, and energy conservation within all electrical systems.
FAQ
In physics, the term work done refers to energy transfer whenever a force moves something through a distance.
In an electrical circuit, charges move through a potential difference, meaning the electric field does work on them.
The amount of work done by the source equals the energy supplied to the charges — this is why W = VIt can also be written as “work done = potential difference × current × time”.
Energy transfer increases linearly with time.
If a device operates for twice as long under the same current and potential difference, it transfers twice as much energy.
This relationship explains why leaving appliances running unnecessarily wastes energy — even small currents cause significant transfer when maintained over long periods.
Fluctuating voltage supply – affects energy calculation directly.
Contact resistance or poor connections – reduce measured current.
Heating effects – change resistance during the test, altering readings.
Human reaction time – introduces uncertainty in manual stopwatch timing.
Minimising these issues with digital meters, data loggers, and stable power supplies improves accuracy in determining W = VIt.
The joule is too small for everyday energy quantities.
A kilowatt-hour (kWh) represents the energy transferred when a 1 kW device operates for 1 hour, equivalent to 3.6 × 10⁶ J.
Using kWh makes domestic energy bills manageable and easier to interpret when calculating cost per unit of energy used.
Energy supplied to a resistor converts mainly into thermal energy due to electron collisions with the lattice of the material.
This process increases the component’s temperature and can be useful (in a heater) or undesirable (in data circuits).
Energy conservation still applies: all electrical energy lost as heat or light equals the total energy transferred by the circuit’s source over time.
Practice Questions
Question 1 (2 marks)
A heater is connected to a 230 V mains supply and draws a current of 5.0 A for 2.0 minutes.
(a) Calculate the energy transferred by the heater in this time.
Mark Scheme:
• Correct equation used: W = V I t (1 mark)
• Substitution and calculation: W = 230 × 5.0 × (2.0 × 60) = 138 000 J (1.38 × 10⁵ J) (1 mark)
Question 2 (5 marks)
A student investigates how much electrical energy is transferred by a lamp. The lamp operates at a potential difference of 12 V and carries a current of 0.50 A.
(a) Derive an expression to calculate the total energy transferred by the lamp over a time period t.
(b) The lamp is left on for 15 minutes. Calculate the total energy transferred and state an appropriate unit.
(c) Explain, using your result, why leaving lights on unnecessarily increases energy costs.
Mark Scheme:
(a)
• Recognises relationship W = V I t (1 mark)
• Explains that energy transfer increases with voltage, current, and time (1 mark)
(b)
• Substitution: W = 12 × 0.50 × (15 × 60) (1 mark)
• Correct calculation: W = 5400 J (5.4 × 10³ J) (1 mark)
• Correct unit: joules or J (1 mark)
(c)
• Clear explanation that greater energy transfer over time means more electrical energy used, increasing total cost (1 mark)
• Links idea to energy billing in kilowatt-hours or to power consumption over time (1 mark)

