In uniform circular motion, understanding period and frequency is essential to describing how objects move at constant speed around a circular path, linking angular and linear motion concepts.

Understanding Period and Frequency

In circular motion, two fundamental quantities describe how fast an object completes rotations — the period and the frequency. These parameters provide insight into how often and how quickly circular motion occurs and are central to analysing repetitive physical systems such as planetary orbits, pendulums, and rotating machinery.

The Concept of Period

The period refers to the time required for an object to make one complete revolution or cycle of circular motion. It quantifies the duration of one full path around the circle and provides a direct measure of time per revolution.

The period is measured in seconds (s), aligning with the SI unit for time. For example, if a rotating object completes each circle in 0.2 seconds, its period is 0.2 s. Shorter periods correspond to faster motion, as the object completes each rotation more quickly.

A useful way to visualise the period is to imagine one complete orbit — such as the Earth revolving around the Sun once every 365 days. That time duration represents the period of Earth’s orbital motion.
The period TTT is the time taken for one complete revolution.

The second hand has period T=60 sT = 60\ \text{s}T=60 s, so its frequency is f=1/T=1/60 Hzf = 1/T = 1/60\ \text{Hz}f=1/T=1/60 Hz. Each full sweep corresponds to one cycle, directly illustrating the reciprocal relationship between period and frequency. This photo shows a standard, clearly marked clock face for easy interpretation. Source.

The Concept of Frequency

Complementary to the period is the frequency, which measures how many complete cycles occur each second. Whereas period looks at “time per revolution,” frequency looks at “revolutions per time.”

Frequency is measured in hertz (Hz), where 1 Hz equals one cycle per second. For instance, a wheel that makes 5 rotations every second has a frequency of 5 Hz.

Frequency is a critical quantity in physics because it expresses how often an event repeats — a concept that extends far beyond circular motion into areas such as waves, sound, and alternating current.

The Relationship Between Period and Frequency

The relationship between period and frequency arises naturally from their definitions. Since one quantity describes cycles per time and the other describes time per cycle, they are reciprocals of one another.

EQUATION
—-----------------------------------------------------------------
Relationship between period and frequency: f = 1 / T
f = frequency in hertz (Hz)
T = period in seconds (s)
—-----------------------------------------------------------------

This simple inverse relationship is fundamental to uniform circular motion and forms the basis for connecting rotational and time-based measurements. If an object takes less time to complete a revolution, its period is smaller, and its frequency is therefore higher.

To maintain consistency in physical reasoning, remember that high-frequency motion corresponds to rapid repetition of cycles, while low-frequency motion corresponds to slow repetition.

Constant Speed and Circular Motion

The OCR specification focuses on objects moving in circles at constant speed. In such motion, the speed — the magnitude of velocity — remains unchanged, but the direction continuously changes as the object moves along the circular path.

Although the object’s velocity changes direction, its speed and therefore its period and frequency remain constant, assuming the motion is uniform. The angular velocity (the rate of change of angular displacement) remains constant under these conditions, directly linking with frequency and period through their mathematical relationships.

Linking Period and Frequency to Angular Velocity

Circular motion involves angular displacement, measured in radians, which quantifies how much of the circle the object covers over time. When the motion is uniform, angular displacement increases steadily, and the angular velocity (ω) represents how fast this angular change occurs.

EQUATION
—-----------------------------------------------------------------
Angular velocity–period relation: ω = 2π / T
ω = angular velocity in radians per second (rad s⁻¹)
T = period in seconds (s)
—-----------------------------------------------------------------

There is also a corresponding form connecting angular velocity with frequency.

EQUATION
—-----------------------------------------------------------------
Angular velocity–frequency relation: ω = 2πf
ω = angular velocity in radians per second (rad s⁻¹)
f = frequency in hertz (Hz)
—-----------------------------------------------------------------

These expressions show that as frequency increases — meaning more rotations per second — angular velocity also increases, resulting in faster rotational motion. Similarly, a longer period means slower rotation and smaller angular velocity.
These quantities are linked to angular velocity by ω=2π/T=2πf\omega = 2\pi/T = 2\pi fω=2π/T=2πf.

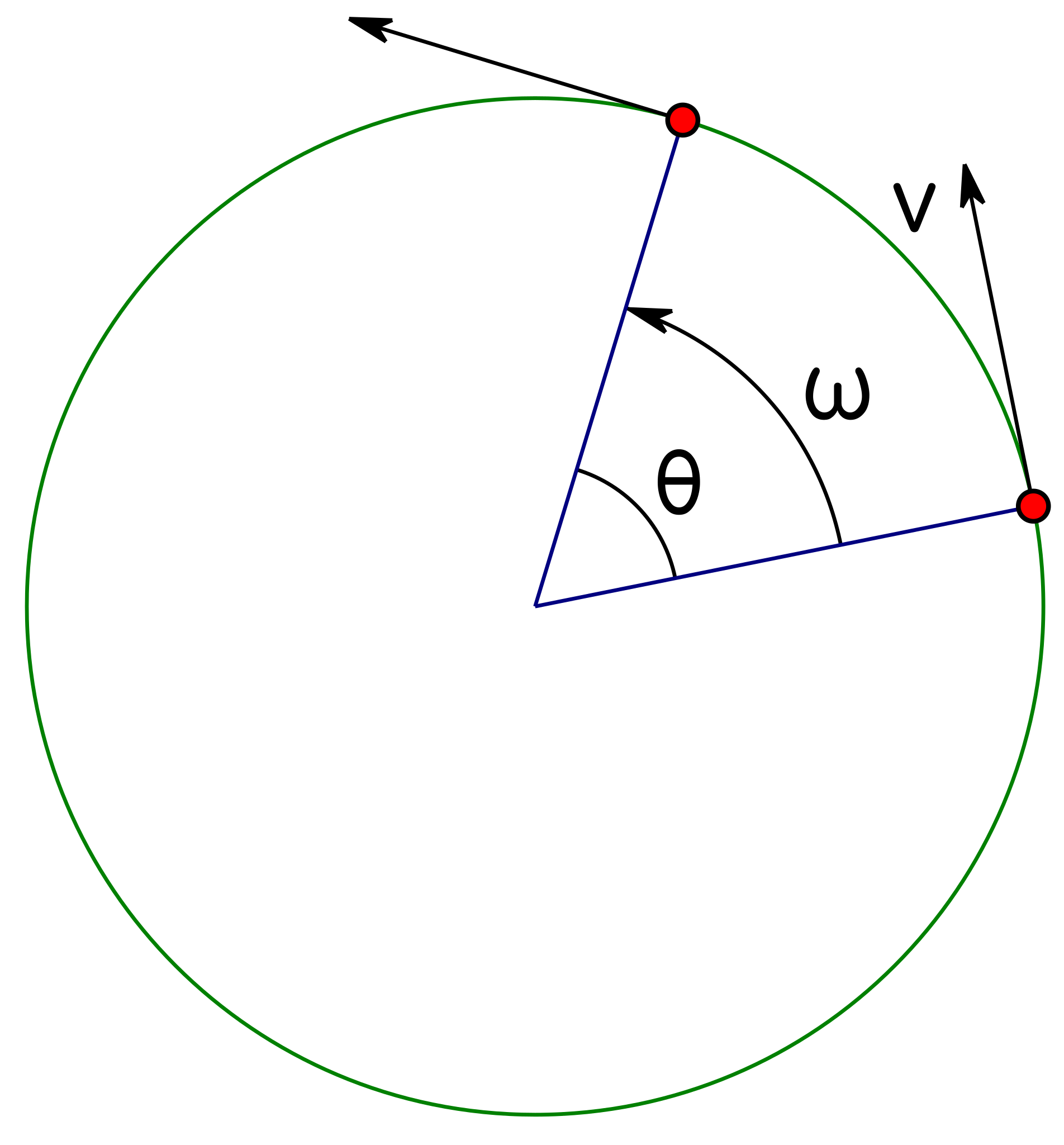
Uniform circular motion with radius rrr, angular displacement θ\thetaθ, angular velocity ω\omegaω, and tangential speed vvv. One full revolution corresponds to θ=2π\theta = 2\piθ=2π and period TTT, so ω=2π/T=2πf\omega = 2\pi/T = 2\pi fω=2π/T=2πf. This diagram also shows vvv as tangent to the path, which is consistent with motion at constant speed. Source.

Interpreting Period and Frequency in Practical Systems

Many physical systems can be analysed by identifying their period and frequency:

• Rotating machinery: Motors, turbines, and fans operate with specific frequencies that determine operational speed and efficiency.

• Orbital motion: Satellites and planets maintain characteristic orbital periods and frequencies, defining their positions and motion patterns.

• Wave motion: Frequency determines oscillation behaviour in sound and light waves, directly linking to pitch and colour.

Each of these systems demonstrates the importance of understanding period and frequency as foundational descriptors of motion.

Factors Affecting Period and Frequency in Circular Motion

While constant speed is assumed in uniform circular motion, real-world conditions may alter the period or frequency. Several factors influence these quantities:

• Radius of motion: For a given angular velocity, increasing the radius lengthens the distance per revolution, potentially affecting linear speed though not directly changing frequency.

• Applied forces: If the centripetal force changes, it may alter angular velocity, leading to adjustments in period and frequency.

• System constraints: Friction, air resistance, or mechanical coupling can slow motion, increasing the period and reducing frequency.

In idealised OCR-style calculations, such complications are usually ignored unless specifically addressed.

Importance of Period and Frequency in Physics

Understanding period and frequency is not merely about computation but about conceptualising repetition and time in motion. These quantities allow physicists to predict the behaviour of dynamic systems, assess rotational stability, and relate linear and angular motion parameters in a coherent mathematical framework.

By mastering period and frequency, students build a foundation for analysing more complex topics such as angular velocity, centripetal acceleration, and wave phenomena, which all rely on the same cyclical principles of time and repetition that define uniform circular motion.