OCR Specification focus:
‘Angular velocity satisfies ω = 2π/T and ω = 2πf for uniform circular motion.’
Angular velocity is a fundamental quantity in circular motion, linking how quickly an object rotates to its period and frequency. Understanding these relationships clarifies rotational motion concepts essential in advanced mechanics.
Angular Velocity and Circular Motion
When studying circular motion, it is essential to describe not only the speed of an object moving around a circle but also how rapidly it completes each rotation. The measure that expresses this rate of rotation is known as angular velocity, denoted by the Greek letter ω (omega). Angular velocity connects the motion’s rotational and linear aspects, forming the foundation for further study of centripetal acceleration and force.
Angular velocity (ω): The rate of change of angular displacement with respect to time. It measures how fast an object rotates around a fixed axis.
In uniform circular motion, an object moves at a constant speed along a circular path, meaning its angular velocity also remains constant.
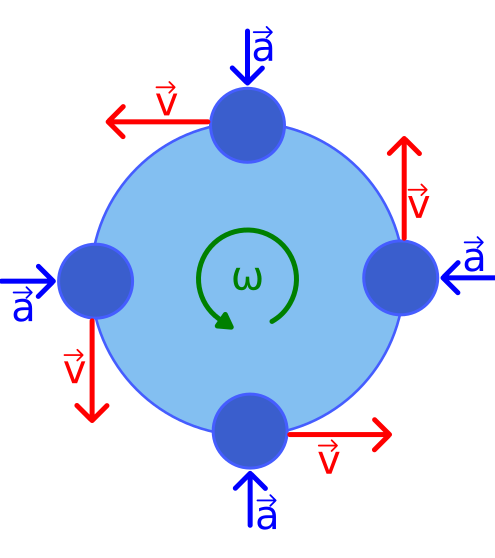
Vector diagram of an object in uniform circular motion showing the angular velocity ω (axial), tangential velocity v (tangent), and centripetal acceleration a (radially inward). This clarifies that ω is constant in uniform motion while v continuously changes direction. Note: the acceleration vector is included for context and will be treated in later subsubtopics. Source.
Each complete revolution corresponds to an angular displacement of 2π radians.

A unit circle labelled in radians and degrees, illustrating that one full rotation is 2π radians. This directly supports the definitions leading to ω = 2π/T and ω = 2πf. Note: the diagram also displays sine/cosine coordinates, which exceed the syllabus requirement but do not affect its usefulness for radian measure. Source.
Angular Displacement and the Concept of a Revolution
Angular displacement describes the angle swept out by a radius from its starting position as the object moves around the circle. Since there are 2π radians in one complete revolution, this value becomes central to expressing angular velocity mathematically. The time taken for one revolution is called the period (T), while the number of revolutions per second is the frequency (f).
These quantities are interrelated and provide two equivalent ways of describing rotational motion — one in terms of time per revolution, and the other in terms of revolutions per second.
The Relationship between Angular Velocity and Period
The period (T) represents the time for one complete revolution. When the object completes one revolution, its angular displacement is 2π radians, and this occurs over a time interval of T seconds. Thus, angular velocity can be defined in terms of period as follows:
EQUATION
—-----------------------------------------------------------------
Angular velocity–period relation (ω = 2π/T)
ω = 2π/T
ω = angular velocity, measured in radians per second (rad s⁻¹)
T = period, measured in seconds (s)
—-----------------------------------------------------------------
This relation demonstrates that the shorter the period, the greater the angular velocity, meaning faster rotational motion. Inversely, a longer period corresponds to a slower rotation. The angular velocity therefore provides a consistent way of comparing circular motions with differing radii and speeds.
After understanding this period-based definition, we can express angular velocity in terms of frequency, another key quantity in oscillatory and circular systems.
The Relationship between Angular Velocity and Frequency
Frequency (f) measures the number of complete revolutions per second. Since one revolution equals 2π radians, the angular velocity is found by multiplying this angular measure by the frequency.
EQUATION
—-----------------------------------------------------------------
Angular velocity–frequency relation (ω = 2πf)
ω = 2πf
ω = angular velocity, measured in radians per second (rad s⁻¹)
f = frequency, measured in hertz (Hz)
—-----------------------------------------------------------------
These two forms — ω = 2π/T and ω = 2πf — are mathematically equivalent because frequency and period are reciprocals (f = 1/T). This equivalence connects the time for a revolution to the number of revolutions per unit time, providing interchangeable ways to calculate angular velocity depending on the given information.
Significance of Angular Velocity Relations
Understanding angular velocity through these relations enables physicists and engineers to:
Describe rotational motion quantitatively, without referring directly to linear speed.
Compare the rotation rates of systems of different radii.
Translate between rotational and oscillatory systems using consistent terminology.
In uniform circular motion, where the object’s speed and radius are constant, angular velocity remains constant in both magnitude and direction (the latter being along the axis of rotation). These relationships form a bridge between linear and angular descriptions of motion, allowing deeper analysis in dynamics and mechanics.
Linear and Angular Quantities
To strengthen understanding, it is useful to recognise how linear velocity relates to angular velocity. Though linear velocity changes direction constantly in circular motion, its magnitude (speed) remains steady. Angular velocity offers a more compact description of this motion by referring only to the rotation rate.
EQUATION
—-----------------------------------------------------------------
Linear–angular velocity relation (v = ωr)
v = ωr
v = linear speed, measured in metres per second (m s⁻¹)
ω = angular velocity, measured in radians per second (rad s⁻¹)
r = radius, measured in metres (m)
—-----------------------------------------------------------------
This relation highlights that for a given angular velocity, an object at a larger radius moves faster linearly. For example, in a rotating wheel, points near the rim travel a greater distance in the same time than points closer to the centre, even though the angular velocity is identical for all points on the wheel.
Direction of Angular Velocity and Measurement
The direction of angular velocity follows the right-hand rule: if the fingers of the right hand curl in the direction of rotation, the thumb points along the direction of the angular velocity vector. This vector representation becomes especially important in three-dimensional rotational analysis and when considering torques and angular momentum later in the course.
In practical applications and experimental setups, angular velocity can be measured using devices such as tachometers or rotational sensors, which count revolutions per second and automatically convert the data into radians per second using ω = 2πf.

A tachometer indicating rotational speed in rpm. Converting rpm to frequency (f = rpm/60) and then to angular velocity (ω = 2πf) links instrumentation to the formulas in this subsubtopic. The photo focuses on the dial and pointer with minimal clutter. Source.
These measurements are fundamental in fields such as mechanical engineering, astronomy, and particle physics.
Applications and Conceptual Context
The relationships ω = 2π/T and ω = 2πf appear repeatedly throughout physics. They link time-based and rotational descriptions and serve as essential groundwork for analysing more complex systems such as:
Rotating machinery — determining safe operating speeds and stresses.
Planetary motion — describing orbital angular velocities.
Wave motion and oscillations — connecting angular frequency to simple harmonic motion.
Centripetal acceleration and force — subsequent subtopics depend on angular velocity to derive further relationships.
By mastering these expressions, students gain a versatile framework for interpreting any rotational or periodic motion encountered in A-Level Physics.
FAQ
Angular velocity is a vector quantity, meaning it has both magnitude and direction. Its direction is along the axis of rotation and follows the right-hand rule.
Angular speed, on the other hand, is the scalar magnitude of angular velocity. It only represents how fast an object rotates, not the direction of rotation.
For uniform circular motion, the angular speed remains constant even though the direction of the angular velocity vector may reverse if the direction of rotation changes.
Radians are the standard angular measure in physics because they simplify mathematical relationships between angular and linear quantities.
When radians are used:
The arc length s equals rθ directly (no conversion factors).
Equations like v = ωr and a = ω²r remain dimensionally consistent.
Using degrees would require inserting conversion factors (π/180), complicating the relationships between physical quantities.
Yes — this occurs when the axis of rotation changes direction.
For example:
A spinning top precessing under gravity maintains constant angular speed about its own axis.
However, because its axis slowly moves, the overall direction of the angular velocity vector changes.
Thus, the magnitude of ω stays constant, but its vector direction changes, meaning angular velocity itself is not constant.
Rotational kinetic energy (Ek) depends on angular velocity through the relationship Ek = ½Iω², where I is the moment of inertia.
This shows that:
Increasing ω greatly increases kinetic energy (since it’s proportional to ω²).
Two objects rotating at the same angular velocity can have different energies depending on their mass distribution (I).
Although this formula lies beyond the immediate subsubtopic, it highlights the physical significance of angular velocity in rotational systems.
In a rigid body, all points rotate through the same angle in the same time about a common axis.
Therefore:
Each point experiences the same angular displacement and hence the same angular velocity ω.
However, their linear speeds differ, since v = ωr — points further from the axis travel faster linearly.
This shared angular velocity allows rotational motion to be described using a single ω, simplifying the analysis of rigid-body dynamics.
Practice Questions
Question 1 (2 marks)
A satellite completes one orbit around Earth every 90 minutes.
Calculate its angular velocity in radians per second.
Mark Scheme:
1 mark for correctly converting 90 minutes into seconds (90 × 60 = 5400 s).
1 mark for correctly applying and calculating using ω = 2π/T → ω = 2π / 5400 = 0.00116 rad s⁻¹ (accept answers between 0.0011–0.0012 rad s⁻¹).
Question 2 (5 marks)
A wheel rotating at a constant angular velocity of 12 rad s⁻¹ has a radius of 0.40 m.
(a) Calculate the frequency and period of rotation. (3 marks)
(b) Explain, using the relationship between angular velocity and linear velocity, how increasing the radius would affect the linear speed of a point on the rim if the angular velocity remains constant. (2 marks)
Mark Scheme:
(a)
1 mark for correctly stating or rearranging ω = 2πf to f = ω / 2π.
1 mark for substitution: f = 12 / 2π = 1.91 Hz (accept 1.9 Hz).
1 mark for using T = 1/f to find T = 0.524 s (accept 0.52 s).
(b)
1 mark for recognising that linear speed is given by v = ωr.
1 mark for stating that if ω is constant, increasing r will increase v proportionally (larger radius → greater linear speed).

