OCR Specification focus:
‘Use the radian as the standard angular measure for circular motion calculations.’
In circular motion, understanding how angles are measured is fundamental. The radian provides a natural, consistent unit linking angular displacement, arc length, and radius, forming the foundation for all circular motion analysis.
The Concept of Angular Measure
Degrees versus Radians
Traditionally, angles are measured in degrees, where a full revolution equals 360°. However, this measure is arbitrary and disconnected from the physical geometry of a circle. The radian provides a more direct and mathematically coherent relationship between arc length and radius, making it essential for analysing circular motion and oscillations in physics.
The Definition of a Radian
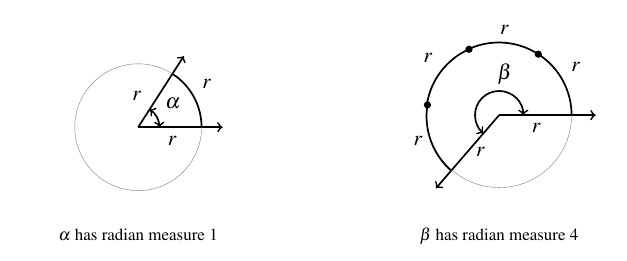
Radian: The angle subtended at the centre of a circle by an arc whose length is equal to the radius of the circle.
The radian is thus based entirely on the intrinsic properties of a circle. This makes it the standard angular measure in physics and mathematics, replacing degrees when performing circular motion calculations.

A central angle θ is measured in radians by the ratio of arc length to radius. When s = r, the angle is 1 rad. This geometric definition underpins s = rθ and all subsequent circular-motion relations. Source.
The Relationship Between Arc Length, Radius, and Angle
For a body moving along a circular path, the arc length (s) represents the distance travelled along the circumference. The radius (r) defines the distance from the centre to any point on the path, while the angle (θ) in radians measures the angular displacement.
EQUATION
—-----------------------------------------------------------------
Arc Length Formula (s) = rθ
s = Arc length (metres, m)
r = Radius of the circle (metres, m)
θ = Angle subtended at the centre (radians, rad)
—-----------------------------------------------------------------
This equation is only valid when the angle θ is measured in radians. It elegantly connects linear motion (through s) with angular motion (through θ). This proportional relationship underpins all further development of circular motion equations, such as angular velocity, centripetal acceleration, and periodic motion relationships.
Visual panels show how radian measure counts radius-lengths along the arc: 1 rad → s = r, 2 rad → s = 2r, etc. The accompanying diagram states θ = s/r and emphasises that s = rθ holds when θ is in radians. This reinforces both the geometric meaning and the correct unit usage for circular-motion calculations. Source.
Why Use Radians in Physics
Radians are preferred in physics because they provide a direct proportionality between linear and angular quantities. When the angular displacement is measured in radians:
The angular velocity (ω), angular acceleration (α), and frequency (f) can be expressed using simple linear relationships.
Derivatives and integrals involving circular motion become mathematically consistent.
Equations describing wave motion, harmonic motion, and rotational kinematics naturally use radians for smooth dimensional coherence.
Dimensional Consistency
When angles are measured in radians, they become dimensionless quantities, since the unit is effectively the ratio of two lengths (arc length divided by radius). This makes the radian compatible with equations involving physical quantities measured in SI units. It ensures that the relationships between linear velocity (v) and angular velocity (ω) or centripetal force (F) are both physically and mathematically sound.
Converting Between Degrees and Radians
Although radians are the standard in physics, students must often convert between degrees and radians for clarity.
EQUATION
—-----------------------------------------------------------------
Conversion Formula (θ) = (π/180°) × θ°
θ = Angle in radians (rad)
θ° = Angle in degrees (°)
—-----------------------------------------------------------------
One complete revolution equals 2π radians, which corresponds to 360°. Therefore:
π radians = 180°
1 radian ≈ 57.3°
These relationships are crucial for translating between descriptive and mathematical forms of circular motion.
Angular Displacement and Radian Measure
Understanding Angular Displacement
Angular Displacement: The angle, measured in radians, through which an object moves around a circular path, taken from a fixed reference line.
Angular displacement is a vector quantity, having both magnitude (the size of the angle) and direction (clockwise or anticlockwise). Using radians allows the angular displacement to directly correspond to arc length, which simplifies analysis of motion around a circle.
The Geometry Behind Radian Measure
To visualise one radian:
Imagine a circle of radius r.
Measure a length of r along the circumference.
The angle formed at the circle’s centre by that arc is 1 radian.
Since the total circumference of a circle is 2πr, the total number of radians in one full revolution is 2π radians. Therefore:
Half a revolution (180°) = π radians
Quarter of a revolution (90°) = π/2 radians
This shows that radians express the natural fraction of a complete rotation, directly linking angular position to distance travelled along the circumference.
Radians in Circular Motion Calculations
In uniform circular motion, quantities such as angular velocity (ω), angular acceleration (α), and period (T) depend on angular measure in radians. For instance:
Angular velocity measures how rapidly angular displacement changes with time, expressed in radians per second.
Angular acceleration describes how angular velocity changes over time, again in radians per second squared.
EQUATION
—-----------------------------------------------------------------
Angular Velocity (ω) = Δθ / Δt
ω = Angular velocity (radians per second, rad s⁻¹)
Δθ = Change in angular displacement (radians, rad)
Δt = Time interval (seconds, s)
—-----------------------------------------------------------------
Using radians ensures that this formula remains dimensionally consistent, and that relationships such as v = ωr and a = ω²r (introduced in later subsubtopics) emerge naturally from basic geometry.
Summary of Key Properties of the Radian Measure
Definition: Based on the ratio of arc length to radius.
Fundamental relationship: s = rθ (valid only if θ is in radians).
Total radians in a full circle: 2π radians.
Advantages:
Dimensionless unit ensuring consistency with SI equations.
Simplifies differentiation and integration in rotational motion.
Provides direct proportionality between linear and angular quantities.
Conversions:
1 rad = 57.3°, π rad = 180°, 2π rad = 360°.
By adopting the radian as the standard angular measure, OCR Physics students gain a unified framework that underpins the mathematical treatment of circular motion, enabling precise and consistent analysis across all rotational phenomena.
FAQ
The radian is based on the geometry of the circle itself rather than an arbitrary division like degrees. It relates arc length directly to radius, meaning one radian equals the angle made when the arc length equals the radius.
This connection makes mathematical relationships in circular motion simpler and dimensionally consistent. It allows equations like s = rθ to work without additional constants, linking linear and angular quantities in a natural, intuitive way.
In the unit circle, the radius is 1 unit. Therefore, the length of the arc is numerically equal to the angle in radians.
For example:
An angle of 1 radian corresponds to an arc length of 1.
π/2 radians (90°) corresponds to an arc length of π/2.
This makes radians fundamental in defining trigonometric functions, since sine, cosine, and tangent values change smoothly with angular displacement measured in radians.
Radians are technically dimensionless, since they are defined as the ratio of two lengths — arc length (m) divided by radius (m). The units cancel, leaving a pure number.
However, radians are given a symbolic unit (rad) to clarify that an angular measure is being used. This helps prevent confusion between linear and angular quantities, even though radians have no physical dimension in SI base units.
When using radians, derivatives and integrals of trigonometric functions behave predictably without scaling factors. For example:
d(sin θ)/dθ = cos θ only holds when θ is in radians.
If θ were measured in degrees, an unwanted factor of π/180 would appear in every differentiation.
This property makes radians essential for formulating equations of motion, wave functions, and rotational dynamics that rely on calculus.
Degrees are sometimes used for descriptive clarity or visual interpretation — for instance, when discussing the rotation of a body (90°, 180°, etc.) or in experimental contexts involving angular positions on apparatus scales.
However, whenever quantitative analysis or equations are involved — such as calculating angular velocity, arc length, or centripetal acceleration — radians must be used. They ensure mathematical and dimensional consistency across all physical relationships.
Practice Questions
Question 1 (2 marks)
Define one radian and state how many radians there are in a complete circle.
Mark Scheme:
(1 mark) Correct definition: The angle subtended at the centre of a circle by an arc equal in length to the radius.
(1 mark) Correct total radians in a circle: 2π radians.
Question 2 (5 marks)
An object moves along a circular path of radius 0.80 m. The arc length travelled is 1.60 m.
(a) Calculate the angular displacement of the object in radians. (2 marks)
(b) Express this angular displacement in degrees. (2 marks)
(c) Explain why radians are preferred to degrees in physics when describing angular motion. (1 mark)
Mark Scheme:
(a)
(1 mark) Correct formula: θ = s / r
(1 mark) Substitution and answer: θ = 1.60 / 0.80 = 2.0 radians
(b)
(1 mark) Correct conversion method: θ° = θ × (180 / π)
(1 mark) Correct answer: θ° = 2.0 × (180 / π) = 114.6° (accept 115° with rounding)
(c)
(1 mark) Clear explanation: Radians give direct proportionality between arc length and radius (s = rθ) and ensure dimensional consistency in circular motion equations.

