OCR Specification focus:
‘The force between two point masses is F = −GMm/r² directed along the line joining them.’
Gravitation governs interactions between masses across the Universe, shaping orbital motion, surface gravity, and cosmic structure. Understanding the inverse-square law of gravitation provides essential insight into how gravitational forces act over distance.
The Inverse-Square Law of Gravitation
The inverse-square law of gravitation describes how the gravitational force between two point masses behaves with separation. It is the foundation of Newtonian gravitational theory and a core model used in A-Level Physics. This law applies specifically to point masses, but it can also be used for spherically symmetric bodies, which behave as though all their mass is concentrated at their centres. The OCR specification states that the force between two point masses is given by the expression F = −GMm/r², and is always directed along the line joining them.
Newton’s Model of Gravitational Interaction
Newton proposed that all masses exert a mutually attractive force on each other. This force does not require physical contact and acts through space as a field force. The strength of the attraction depends on the masses involved and the distance separating them. Because this force acts at all distances, gravitational effects extend infinitely, though they become extremely small as separation increases.
Gravitational Force and Attraction
When two masses interact gravitationally, each experiences an equal and opposite force. This aligns with Newton’s third law and is a fundamental feature of any central force system. The fact that the force is always attractive distinguishes gravity from other forces such as the electrostatic force, which may be attractive or repulsive. The force between two point masses is always attractive and acts along the straight line joining their centres.
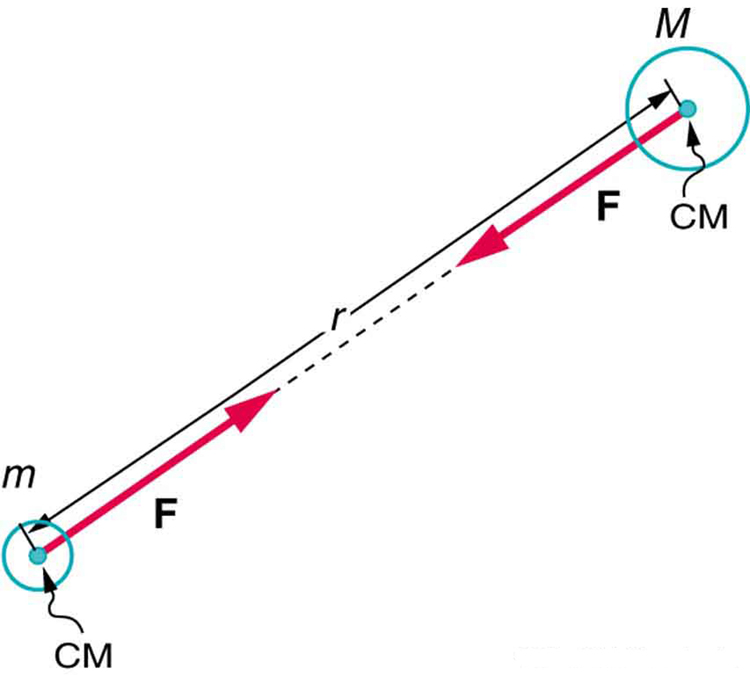
Two point masses M and m are separated by a distance r, with equal and opposite gravitational forces F acting along the line joining their centres. This illustrates that Newtonian gravitation is a central, attractive force depending only on the masses and their separation. The diagram also reinforces that each mass feels the same magnitude of force, consistent with Newton’s third law, without introducing any concepts beyond this subtopic. Source.
One immediate implication of the inverse-square relationship is that gravitational force decreases rapidly with distance. Doubling the separation reduces the force to a quarter of its original value.
EQUATION
—-----------------------------------------------------------------
Newton’s Law of Gravitation (F) = −GMm/r²
F = Gravitational force between the masses, in newtons (N)
G = Gravitational constant, 6.67 × 10⁻¹¹ N m² kg⁻²
M = Mass of the larger or first body, in kilograms (kg)
m = Mass of the second body, in kilograms (kg)
r = Separation between the centres of mass of the bodies, in metres (m)
—-----------------------------------------------------------------
The negative sign emphasises direction: gravitational force acts towards the other mass, consistent with the attractive nature of the interaction.
Modelling Point Masses
For the inverse-square law to be applied accurately, the interacting bodies must either be true point masses or spherically symmetric objects. Spherical symmetry allows a large body such as a planet to be modelled mathematically as a single point at its centre. This approximation is essential for planetary physics and greatly simplifies calculations of force and orbital motion.
Direction of the Gravitational Force
The gravitational force acts along the line joining the centres of the two masses. This makes gravity a central force. Central forces always point towards or away from a fixed point and are essential for producing circular or elliptical orbits. The inverse-square form ensures that planets sweep out equal areas in equal times, linking directly to Kepler’s laws of planetary motion.
Key Characteristics of the Inverse-Square Law
To strengthen conceptual understanding, the following features highlight the essential nature of Newton’s gravitational law:
Proportionality and Dependence
The force is directly proportional to each interacting mass; increasing either mass increases the force.
The force is inversely proportional to the square of distance; small separations generate significantly larger forces.
The gravitational constant G sets the overall strength of gravitational interaction throughout the Universe.
Only the distance between centres matters, not the physical size of the objects.
A direct result of these dependencies is that gravitational interactions between astronomical bodies are very strong compared to those between everyday objects. The enormous masses of planets, stars, and moons create significant gravitational effects even across vast distances.
Consequences of the Inverse-Square Form
Predictability of orbits: Stable planetary and satellite orbits arise naturally from the 1/r² dependence.
Variation of gravitational field strength: Field strength decreases with distance in exactly the same way as force, reinforcing the connection between gravitational fields and gravitational forces.
Universality: The same law applies anywhere in the Universe, from Earth’s surface to distant galaxies.
Mapping the Force in Physical Situations
In real scenarios, gravitational interactions often involve multiple bodies. However, Newton’s law allows physicists to analyse complex systems by considering pairwise interactions or by applying vector addition of forces. Because the gravitational force is central and attractive, the resulting motion of bodies tends to be curved or orbital rather than linear.
Bullet points can help summarise how to apply the law in practical reasoning:
Identify each mass involved and treat spherical bodies as point masses.
Measure or define the separation between their centres.
Apply the inverse-square relationship to determine the force magnitude.
Assign direction along the line joining the masses.
Use vector analysis when more than two masses exert forces simultaneously.
This inverse-square dependence means that if the separation doubles, the gravitational force becomes one quarter of its original value.
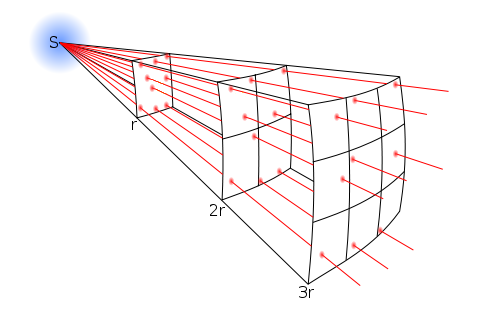
This diagram illustrates the inverse-square law, with the effect of a central source spreading so that its intensity falls as 1/r² with distance r. For gravity, this same pattern describes how the magnitude of the gravitational force between two point masses rapidly decreases as their separation increases. The image is general and refers to intensity rather than gravitational force specifically, but the mathematical relationship is identical to that used in Newton’s law of gravitation. Source.
Gravitation’s inverse-square nature remains one of the fundamental principles underpinning modern physics, enabling accurate prediction of motion from laboratory scales to astronomical phenomena.
FAQ
The inverse-square dependence ensures that as a body moves closer to the mass attracting it, the force increases in a predictable way that allows orbital speeds to adjust smoothly. This relationship naturally produces closed orbits such as circles and ellipses.
If the force did not follow a 1/r² pattern, orbits would not be stable; many alternative force laws either cause spiralling into the central mass or drifting away. Newton showed that only an inverse-square central force produces the orbital shapes observed in planetary systems.
The value of G determines the absolute strength of gravitational interactions. Although gravity is weak compared with other fundamental forces, a larger value of G would lead to much stronger attraction at all distances.
A different G would radically alter cosmic structure:
Larger G: faster star formation, shorter stellar lifetimes, tighter orbits.
Smaller G: weaker binding of galaxies, difficulty forming stars, reduced influence over large distances.
A spherically symmetric body exerts gravitational effects exactly as if its entire mass were concentrated at its centre. This result follows from a mathematical property of spherical symmetry.
The mass outside any imagined spherical shell contributes no net gravitational force on an object inside it, while the enclosed mass behaves like a single point mass. This makes planets, stars, and moons compatible with the inverse-square form despite their size.
Newton’s inverse-square law assumes non-relativistic speeds and moderate gravitational fields. At extremely high speeds or in very strong fields, relativistic effects become significant.
In such cases:
The Newtonian formula becomes an approximation.
Corrections predicted by general relativity describe stronger or differently shaped gravitational fields.
For A-Level purposes, these scenarios lie outside the specification but explain why the Newtonian model eventually breaks down.
Yes. The gravitational forces from several masses combine through vector addition, meaning the total force is the sum of all individual inverse-square contributions.
Important points:
Each interacting pair follows F = GMm/r² separately.
The directions of the forces matter; they rarely act along the same line.
The resulting motion can be complex, especially in three-body systems, but the underlying pairwise law remains unchanged.
Practice Questions
Question 1 (2 marks)
Two point masses, 3.0 kg and 5.0 kg, are separated by a distance r.
State how the gravitational force between them changes if the separation is doubled.
Explain your answer.
Question 1 (2 marks)
• States that the force becomes one quarter of its original value when the separation is doubled (1)
• Explains that this is because gravitational force is inversely proportional to the square of distance between the masses (1)
Question 2 (5 marks)
A planet of mass M orbits a star of mass S.
Using Newton’s law of gravitation, describe the nature of the gravitational force between the two bodies and explain how this force determines the planet’s orbital motion.
In your answer, you should refer to:
• the direction of the gravitational force
• the inverse-square relationship
• how the magnitude of the force changes with distance
• why this force results in orbital motion.
Question 2 (5 marks)
• States that the force is attractive and acts along the line joining the centres of the two bodies (1)
• Mentions that the force follows an inverse-square law, proportional to 1/r² (1)
• States that increasing distance reduces the gravitational force significantly (1)
• Explains that the mutual gravitational force on the planet acts as a centripetal force (1)
• States that this force causes the planet to follow a curved, typically elliptical or circular, orbit around the star (1)

