OCR Specification focus:
‘Use W = F s cosθ for work by a constant force; interpret negative and zero work cases.’
Work done by a force is fundamental in physics, linking force, displacement, and energy transfer. This concept quantifies how energy moves or changes within a system due to applied forces.
Understanding Work and Energy Transfer
In physics, work measures the energy transferred when a force moves an object through a displacement. When a force acts on an object, it can change the object’s kinetic or potential energy depending on the situation. The concept is essential because it connects mechanical action to energy transformations.
When a constant force acts over a displacement, the amount of energy transferred depends not only on the size of the force and the distance moved but also on the angle between the force and the displacement. This relationship is mathematically expressed by the equation W = F s cosθ.
Defining Work
Work: The energy transferred when a force moves an object through a displacement in the direction of that force.
Work is a scalar quantity, meaning it has magnitude but no direction. However, the sign of the work (positive, negative, or zero) is meaningful, as it indicates the direction of energy transfer between the system and its surroundings.
The Work Done by a Constant Force
When a constant force is applied to an object, the work done depends on the component of the force that acts along the direction of motion. The product of this component and the displacement gives the total work done.
EQUATION
—-----------------------------------------------------------------
Work Done by a Force (W) = F s cosθ
F = magnitude of the applied force (newton, N)
s = displacement of the object in the direction of the force (metre, m)
θ = angle between the force and the displacement (degrees or radians)
W = work done (joule, J)
—-----------------------------------------------------------------
This equation shows that only the component of force parallel to the displacement contributes to the work done. The cosθ term adjusts the total work according to how aligned the force and displacement are.
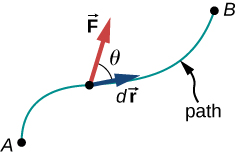
A vector diagram illustrating work as the dot product of force and displacement. The angle θ between F and dr determines the cos θ factor, so only the parallel component transfers energy. This clean schematic mirrors the definition used for constant forces. Source.
Interpreting the Angle θ
The angle θ is crucial to understanding how much of the applied force contributes to energy transfer. Depending on its value:
θ = 0°: The force and displacement are in the same direction.
→ cos0° = 1, so W = F s.
→ The force does the maximum possible work on the object.0° < θ < 90°: The force acts partially in the direction of motion.
→ cosθ is positive but less than 1, so W < F s.
→ The object gains some energy, but not all the force contributes.θ = 90°: The force is perpendicular to displacement.
→ cos90° = 0, so W = 0.
→ The force does no work because it doesn’t change the object’s speed or energy.
Example: The normal reaction force on a sliding object.
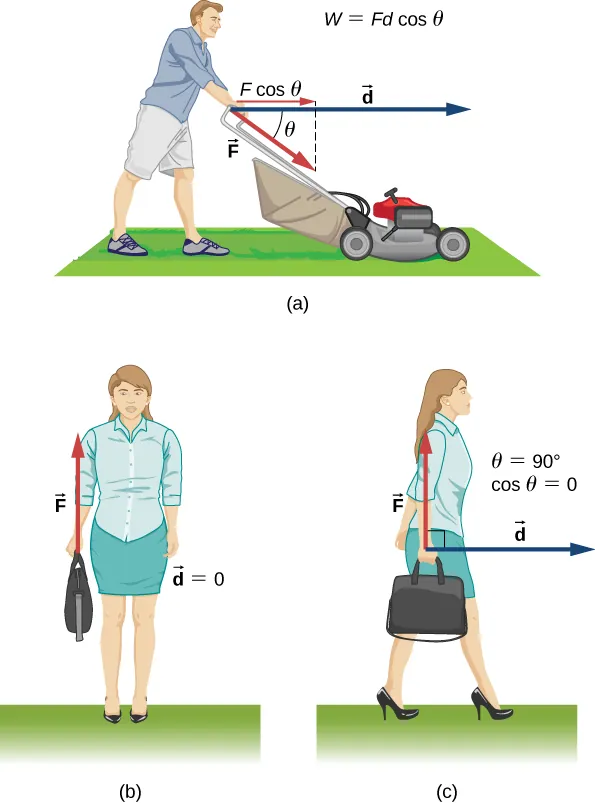
Work by a constant force: (a) Parallel component of the push on a lawn mower gives W = Fd cosθ. (b) No displacement → zero work. (c) Force perpendicular to displacement → zero work because cos 90° = 0. (This figure also includes everyday contexts beyond the abstract diagram, which is acceptable and helpful for interpretation.) Source.
90° < θ < 180°: The force acts opposite to motion.
→ cosθ is negative, so W < 0.
→ The force removes energy from the object (e.g., friction slowing motion).
The Joule as the Unit of Work
The joule (J) is the SI unit of work and energy.
Joule: The work done when a force of one newton moves an object one metre in the direction of the force.
1 J = 1 N m.
This definition directly connects the joule to the newton and metre, reinforcing that work is an energy transfer resulting from motion caused by a force.
Positive, Negative, and Zero Work
The sign of the work indicates the direction of energy transfer:
Positive work: Energy is transferred to the object, increasing its kinetic or potential energy.
Example: A person pushing a box forward.Negative work: Energy is transferred from the object to another system, reducing its energy.
Example: Friction opposing motion or brakes slowing a car.Zero work: No energy transfer occurs through the force, even if the force is large.
Example: A satellite moving in orbit under a gravitational force at right angles to its motion.
These interpretations are vital in analysing energy conservation within systems and understanding where energy is stored or lost.
Conceptual Link to Energy Transfer
Work is fundamentally about energy change. When work is done on an object, the object’s energy increases. When the object does work on another system, its energy decreases. In mechanical processes, the amount of work done equals the energy transferred, maintaining the principle of conservation of energy.
The W = F s cosθ relationship provides a direct bridge between forces and energy changes, allowing physicists to quantify how mechanical actions lead to changes in motion or potential.
Applying the Work Equation in Real Contexts
When analysing systems:
Always identify the direction of both the force and displacement.
Resolve forces into components parallel and perpendicular to motion.
Apply W = F s cosθ to the parallel component only.
Use sign conventions carefully to distinguish between energy input and output.
A block on a horizontal surface pulled by a force F at angle θ. The parallel component Fcosθ does work over displacement s; the perpendicular component does no work on the translation. (This diagram may include arrows/components beyond those explicitly named in the syllabus; these extras simply label the same quantities and remain within scope.) Source.
This approach ensures consistent and correct analysis of energy transfer, whether in mechanics, electricity, or thermodynamics.
Relationship Between Work, Force, and Displacement
The relationship W = F s cosθ shows that work is proportional to both force magnitude and distance moved in the relevant direction. If either factor is zero, the work done is zero. Thus:
No displacement → no work.
No force component along motion → no work.
Opposing force → negative work, representing energy removal.
Understanding this relationship helps explain real-world phenomena such as acceleration, deceleration, and constant-speed motion under balanced forces.
Summary of Key Points for Study
Work quantifies energy transfer by a force through displacement.
Only the component of force parallel to motion performs work.
The equation W = F s cosθ is central to calculating mechanical work.
Positive, negative, and zero work describe different directions of energy flow.
The joule (J) represents one newton-metre of work done.
These principles underpin many later topics, including kinetic energy, potential energy, and power, making them foundational to understanding energy transformations in physical systems.
FAQ
The direction of displacement determines whether the work done is positive, negative, or zero.
If displacement is in the same direction as the force, work is positive — the object gains energy.
If displacement is opposite to the force, work is negative — energy is taken from the object.
If displacement is perpendicular to the force, work is zero, since the force doesn’t contribute to movement in that direction.
The displacement’s direction relative to the force is therefore essential when analysing energy transfer.
A centripetal force acts towards the centre of the circle, while the object’s velocity (and therefore its displacement) is tangential to the path.
Since the force is always perpendicular to the displacement at any instant, the angle between them is 90°.
This makes cos90° = 0, and therefore no work is done — even though the object’s direction changes, its speed and kinetic energy remain constant.
Yes. Work may be done without visible motion when energy is transferred in other forms.
For example:
Compressing a spring involves displacement, but not necessarily an increase in velocity — energy is stored as elastic potential energy.
Lifting an object slowly at constant speed involves work against gravity, even though kinetic energy doesn’t change.
In both cases, the work done alters the object’s energy store, not necessarily its speed.
Forces rarely act perfectly along an object’s path. The parallel component of the force is the part responsible for changing the object’s energy or speed.
The perpendicular component does not contribute to motion along the displacement.
Ignoring the angle leads to overestimating the work done and incorrect energy calculations.
Hence, resolving forces into parallel and perpendicular components ensures accurate analysis of work and energy transfer.
When friction acts, part of the mechanical work done by an applied force is converted into thermal energy.
The frictional force opposes motion, doing negative work on the object.
The energy lost from the object’s motion becomes heat in the contact surfaces and surroundings.
Therefore, in real systems, total work done by applied forces is split between useful work (energy transfer to motion) and dissipated work (energy lost as heat).
Practice Questions
Question 1 (2 marks)
A constant force of 20 N acts at an angle of 30° to the direction of motion of a box. The box is displaced by 4.0 m along a horizontal surface.
(a) Calculate the work done by the force on the box.
Question 1 (2 marks)
• Correct use of formula: W = F s cosθ (1 mark)
• Substitution and calculation: W = 20 × 4.0 × cos30° = 69.3 J (accept 69 J or 69.3 J) (1 mark)
Question 2 (5 marks)
A person pulls a sledge along a flat, snowy surface with a rope making an angle of 40° to the horizontal. The tension in the rope is 50 N, and the sledge moves a distance of 15 m at a constant speed.
(a) Calculate the work done by the person on the sledge.
(b) Explain why the kinetic energy of the sledge does not increase even though work is done on it.
(c) The frictional force between the sledge and the snow is 38 N. Determine the work done against friction and state the net work done on the sledge.
Question 2 (5 marks)
(a)
• Correct formula: W = F s cosθ (1 mark)
• Substitution and calculation: W = 50 × 15 × cos40° = 575 J (accept 574–576 J) (1 mark)
(b)
• Explanation that the sledge moves at constant speed, so there is no change in kinetic energy (1 mark)
• Work done by the person is balanced by work done against frictional forces (1 mark)
(c)
• Work done against friction = friction × distance = 38 × 15 = 570 J (1 mark)
• Net work done = 575 – 570 = 5 J (approximately zero, confirming constant speed) (1 mark)

