OCR Specification focus:
‘Define mechanical work and the joule; relate work to energy transfer in systems.’
Work and energy describe how forces cause movement and transformation in physical systems. Understanding their relationship enables physicists to explain motion, energy transfer, and mechanical processes effectively.
The Concept of Work
In physics, work refers to the process of transferring energy through the action of a force applied over a distance. It connects the ideas of force, motion, and energy. Work is done whenever a force causes an object to move in the direction of that force. If no movement occurs, or if the force is perpendicular to the displacement, then no work is done.
Work: The transfer of energy that occurs when a force acts on an object to move it in the direction of the force.
Work measures how effectively a force contributes to motion and energy change. The concept applies broadly — from lifting a weight to accelerating a vehicle or stretching a spring.
Mechanical Work and the Joule
The joule (J) is the SI unit of both work and energy, showing that these quantities are fundamentally linked. One joule represents the amount of work done when a force of one newton moves an object through one metre in the direction of the force.
Joule (J): The work done or energy transferred when a force of 1 newton moves its point of application 1 metre in the direction of the force.
This equivalence between work and energy means that performing work on an object either increases its energy or changes the form of energy within a system. The mechanical work done on a body is, therefore, directly proportional to the energy transferred to or from that body.
Relationship Between Work and Energy Transfer
Energy can exist in many forms — kinetic, potential, thermal, electrical, and others. When work is done, energy is transferred between objects or transformed between these forms. This relationship is central to the principle of energy conservation, which states that energy cannot be created or destroyed, only converted or transferred.
When work is done on an object:
The object gains energy (for example, increasing its kinetic or potential energy).
The work done by the external agent is positive.
When work is done by an object:
The object loses energy.
The work done is negative from the object’s perspective.
Thus, work is the quantitative measure of energy transfer in mechanical systems. This understanding underpins much of classical physics and engineering.
Quantifying Mechanical Work
The amount of work done depends on three factors:
The magnitude of the force (F) applied.
The displacement (s) of the object.
The direction of the force relative to the displacement.
EQUATION
—-----------------------------------------------------------------
Work Done (W) = Force (F) × Distance moved (s) × cos(θ)
W = Work done, measured in joules (J)
F = Force applied, measured in newtons (N)
s = Displacement of the object in the direction of the force, measured in metres (m)
θ = Angle between the force and displacement vectors, measured in degrees or radians
—-----------------------------------------------------------------
This equation expresses that only the component of the force acting in the direction of motion contributes to work. A perpendicular force (θ = 90°) does no work, because it does not cause motion along its line of action.
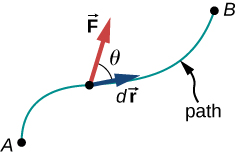
Figure shows a particle moving along a path from A to B with an infinitesimal displacement dr and an applied force F at angle θ to the path. Work arises from the dot product F·dr, so only the component of F parallel to dr contributes. The diagram includes calculus notation for variable force, which goes slightly beyond this subsubtopic but clarifies direction and magnitude relationships. Source.
Positive, Negative, and Zero Work
Positive Work
When the force and displacement are in the same direction, work is positive. Energy is transferred to the object.
Examples:
Pushing a trolley forward.
Gravity accelerating a falling object.
Negative Work
When the force acts opposite to the direction of motion, work is negative. Energy is taken from the object.
Examples:
Friction opposing motion.
A person slowing a moving cart.
Zero Work
When the force is perpendicular to displacement or when no displacement occurs, no work is done.
Examples:
Centripetal force in circular motion (force is perpendicular to velocity).
Carrying an object at constant height with no vertical movement.
These cases highlight that work depends not only on the size of the force but on its direction relative to motion.
A perpendicular force (θ = 90°) does no work, because it does not cause motion along its line of action.
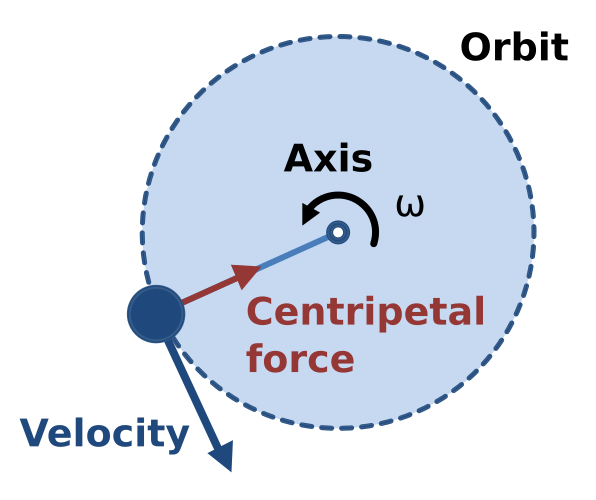
Object in uniform circular motion with tangential velocity v and inward centripetal force. Because the force is perpendicular to the instantaneous displacement, the work done by the force is zero. The circular-motion detail extends beyond the core definition but neatly demonstrates the θ = 90° condition for zero work. Source.
The Physical Interpretation of Work
Work represents a mechanism of energy transfer. It bridges the concepts of force and energy. When a force acts through a displacement:
Mechanical energy (kinetic and potential) of a system may change.
Internal energy may increase (e.g. through friction converting mechanical energy into heat).
Because energy and work share the same unit, the joule, they are quantitatively equivalent descriptions of physical change. Whenever energy changes hands or form, work has been done somewhere in the system.
Work in Different Contexts
Work applies to many real-world and theoretical contexts in physics:
Linear motion: A car engine does work to overcome resistive forces and increase the vehicle’s kinetic energy.
Vertical motion: When an object is lifted, work is done against gravity, increasing its gravitational potential energy.
Elastic deformation: Stretching a spring involves work stored as elastic potential energy.
Thermodynamic systems: Work can also involve pressure and volume changes, where mechanical energy is transferred by moving pistons or gases.
In every case, the same physical idea applies: work equals energy transfer resulting from a force acting through a displacement.
Measuring and Interpreting Work
In experimental or applied physics, measuring work helps quantify energy changes in a system. To calculate total work:
Resolve forces into components along the direction of motion.
Sum the contributions of each force.
Account for resistive and frictional effects when appropriate.
Work measurements provide insight into:
Efficiency — how much input energy becomes useful output.
Energy losses — due to heat, sound, or deformation.
System dynamics — revealing how forces interact to produce motion or stability.
Understanding the concept of work and the joule enables students to analyse complex physical systems in terms of energy transfer, force, and motion, forming the foundation for the study of mechanics and energy principles throughout physics.
FAQ
Mechanical work involves a force acting through a displacement, such as pushing, pulling, or lifting an object. It always requires motion in the direction of a component of the force.
Non-mechanical energy transfers occur without macroscopic motion, for example:
Heating: energy transferred due to a temperature difference.
Electrical transfer: energy moved by charges in an electric circuit.
Both processes involve energy changes but do not fit the mechanical definition of work.
When you carry an object at constant speed and height, the force you exert is vertical (supporting its weight), while the displacement is horizontal.
Since the force and displacement are perpendicular, the angle θ = 90°, and cos(90°) = 0, meaning no mechanical work is done against gravity. Energy is only transferred if the object is lifted or lowered.
Yes. If the work done changes another form of energy instead of kinetic energy, total energy still changes.
Examples include:
Elastic deformation: work stored as elastic potential energy.
Heating by friction: mechanical work converted to thermal energy.
Thus, work represents energy transfer, not just a change in speed or motion.
Work and energy share the same physical dimensions — they both quantify energy transfer.
1 joule equals 1 newton metre (1 J = 1 N m), the work done when a 1 N force moves an object 1 m in the direction of that force.
Using the same unit highlights that doing work and transferring energy are two descriptions of the same physical process.
A common method is using a force–displacement graph.
The area under the graph represents the work done.
If the force is constant, this area forms a rectangle: W = F × s.
For variable forces, the total work equals the area under the curve.
This graphical method provides an intuitive way to determine work, even when force changes with displacement.
Practice Questions
Question 1 (2 marks)
Define the term work in physics and state its SI unit.
Mark scheme:
1 mark: States that work is the energy transferred when a force moves an object through a distance in the direction of the force.
1 mark: States that the SI unit of work is the joule (J).
Question 2 (5 marks)
A student pulls a sled across flat ground with a constant horizontal force of 50 N. The sled moves 12 m in the direction of the force.
(a) Calculate the work done by the student on the sled. (2 marks)
(b) The sled is then pulled at the same speed over rougher ground where the frictional force is 30 N opposing motion. Explain, using the concept of work and energy transfer, how the total work done and energy transfer differ in this case. (3 marks)
Mark scheme:
(a)
1 mark: Correct use of equation W = F s cosθ.
1 mark: Correct numerical answer: W = 50 × 12 = 600 J (accept 600 joules).
(b)
1 mark: Recognises that friction does negative work or work is done against friction.
1 mark: States that some energy is transferred to thermal energy of the sled and ground (not all remains as useful mechanical energy).
1 mark: States that the total work done by the student increases, but the useful energy transferred to motion is reduced because of energy losses to heat.

