OCR Specification focus:
‘Explain that energy transferred to a system equals work done on it in mechanical processes.’
In mechanics, the equivalence of energy transfer and work done links physical movement and energy flow, revealing how forces cause measurable energy changes within and between systems.
Understanding Work and Energy Transfer
The Concept of Work
When a force acts on an object and causes displacement, work is said to be done. Work quantifies the mechanical interaction between a force and motion. Energy is transferred whenever work is done—this fundamental equivalence is central to all mechanical processes.
Work: The energy transferred when a force causes an object to move through a displacement in the direction of that force.
Everyday examples, such as lifting a book or compressing a spring, illustrate how applying a force leads to energy transfer from one form or system to another. In each case, the energy gained by the system equals the work done on it, assuming no losses to other forms like heat or sound.
The Principle of Energy Transfer
In physics, energy transfer describes the movement of energy from one store to another, such as from chemical energy in muscles to kinetic energy in a moving object. The work-energy equivalence means that the amount of energy transferred to an object is numerically equal to the work done on it.
When a force acts, it changes the energy content of a system. This could be an increase in kinetic energy, potential energy, or internal energy, depending on the process involved.
Mechanical Work and System Energy
Applying the Equivalence
The equivalence principle states that in a mechanical process, the total energy transferred to a system equals the total work done on it. This relationship assumes the system is closed—meaning no energy enters or leaves except via work or heat.
For instance, when a person pushes a trolley and it accelerates, the work done by the person’s force results in an equivalent increase in the trolley’s kinetic energy. Similarly, when an object is lifted vertically, the work done against gravity equals the gain in gravitational potential energy.
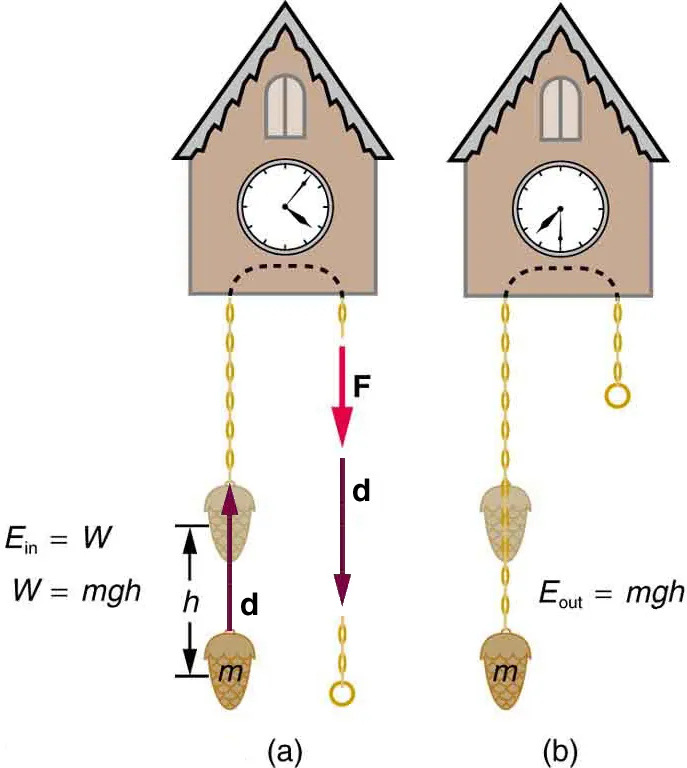
Two-panel schematic of a raised weight: panel (a) shows positive work done against gravity storing mgh in the Earth–object system; panel (b) shows the same mgh released as useful output. The diagram reinforces that energy transferred to the system equals work done on it. Minor additional context (cuckoo-clock mechanism) is included but does not exceed syllabus scope. Source.
EQUATION
—-----------------------------------------------------------------
Work Done (W) = Force (F) × Displacement (s) × cosθ
F = Force applied (newton, N)
s = Displacement in the direction of force (metre, m)
θ = Angle between force and displacement
W = Work done (joule, J)
—-----------------------------------------------------------------
The work-energy equivalence can therefore be expressed as:
EQUATION
—-----------------------------------------------------------------
Energy Transferred (ΔE) = Work Done (W)
ΔE = Change in energy of the system (joule, J)
W = Mechanical work done on or by the system (joule, J)
—-----------------------------------------------------------------
This simple but powerful equation forms the quantitative link between force, motion, and energy in all physical systems.
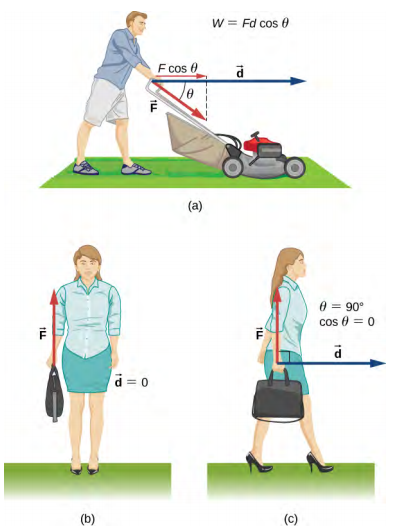
A labelled diagram showing a constant force acting at an angle θ to the displacement, with W = F d cos θ highlighted. It clarifies that only the component of force parallel to displacement transfers energy, while any perpendicular component does no mechanical work. Source.
Energy Pathways in Mechanical Processes
Direction of Energy Transfer
Energy transfer can occur to or from a system:
Work done on a system: Energy is transferred into the system. For example, compressing a gas with a piston increases the internal energy of the gas.
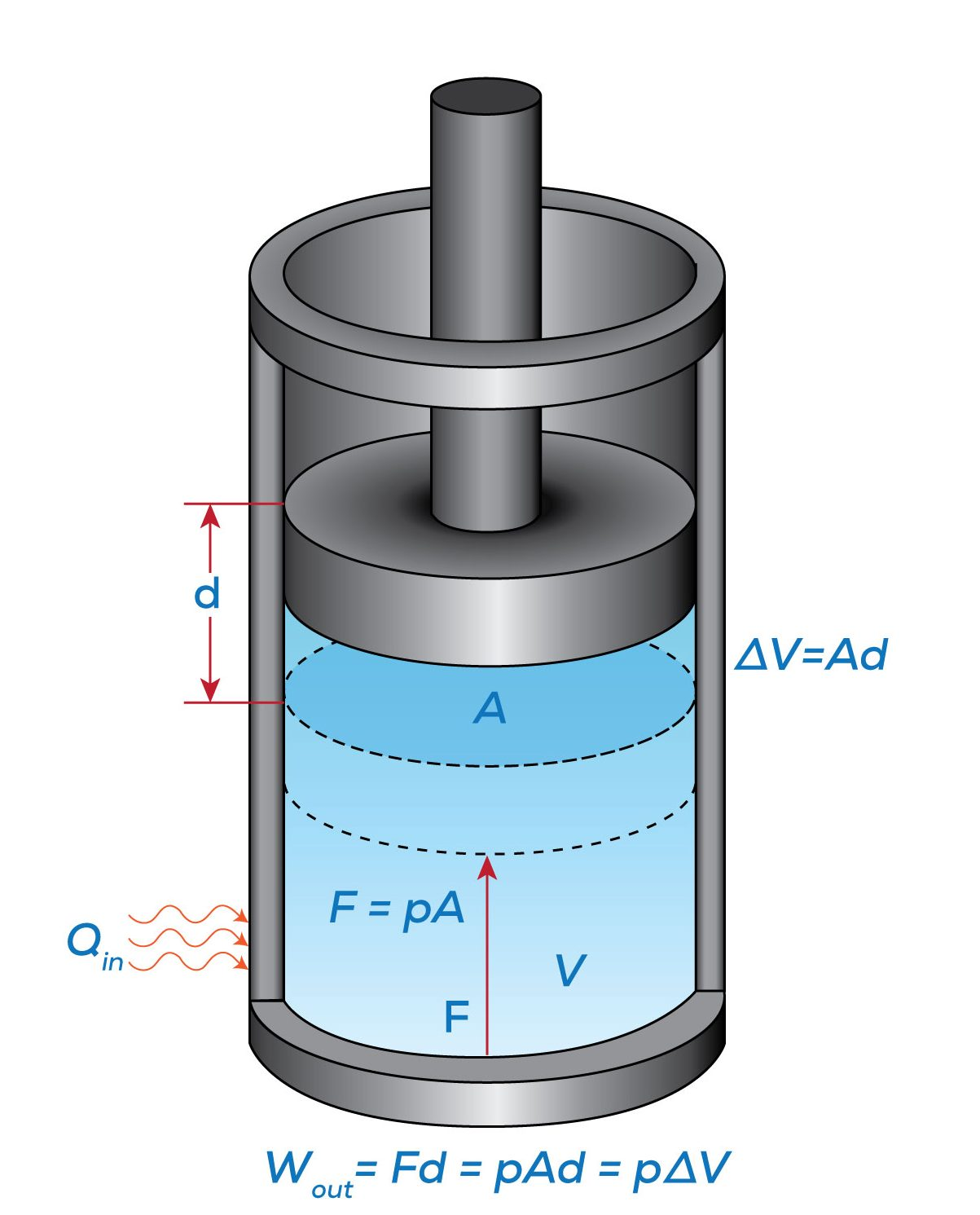
Diagram of a piston–cylinder where gas expansion does positive work on the surroundings and compression corresponds to work done on the gas. It visually anchors the sign convention and the idea that mechanical work is an energy transfer pathway across the boundary. The figure includes PV-work context; this is slightly beyond the A-level syllabus but clarifies direction and sign without unnecessary detail. Source.
Work done by a system: Energy is transferred out of the system. For instance, a gas expanding against a piston performs work on its surroundings.
The sign convention in physics reflects this:
Positive work: Energy is added to the system.
Negative work: Energy leaves the system.
Closed and Open Systems
In a closed system, total energy remains constant—energy may change form but cannot be created or destroyed. All changes are due to internal transfers through work or heat.
In contrast, an open system can exchange both matter and energy with its surroundings. The work-energy equivalence still applies to each individual transfer process but may not represent the total energy change of the open system.
Example Pathways (Conceptually)
Although no worked examples are included here, understanding the following pathways conceptually is vital:
Lifting an object: Work done against gravity transfers energy into gravitational potential energy.
Accelerating a car: Work done by the engine transfers chemical energy into kinetic energy.
Compressing a spring: Work done on the spring transfers energy into elastic potential energy.
In all these cases, the energy gained equals the work done, consistent with the principle of equivalence.
Internal Energy and Non-Mechanical Transfers
Extending the Equivalence
Even in systems where mechanical motion is not obvious, the principle holds. For example, when friction acts between surfaces, mechanical work is converted into thermal energy, raising internal energy. The total energy transferred (as heat) is still equivalent to the work done by frictional forces.
This underlines that work and energy transfer are two descriptions of the same physical process—one expressed in mechanical terms, the other in energy terms.
Energy Conservation Connection
The equivalence of work and energy transfer directly supports the principle of conservation of energy: energy cannot be created or destroyed but only transferred or transformed. Whenever work is done, energy moves from one form or store to another, maintaining total energy constancy in the universe.
Practical Relevance and Conceptual Understanding
Why Equivalence Matters
Understanding this equivalence is crucial because it links forces, motion, and energy in a unified framework. It enables physicists and engineers to:
Quantify energy requirements or outputs for mechanical systems.
Predict how forces alter energy states in structures or machines.
Identify and reduce unwanted energy transfers (for instance, to heat through friction).
Common Misconceptions
Students often confuse energy transfer with energy transformation. Transfer refers to movement of energy between systems, while transformation refers to a change in form within a system. The equivalence discussed here concerns transfer, specifically through mechanical work.
Additionally, energy is not a substance or fluid; it is a property of a system that changes according to the work done and forces acting upon it. Recognising this avoids misconceptions about where energy “goes” during mechanical processes.
In summary (but not as a conclusion), the equivalence of energy transfer and work done forms the foundation for understanding how physical interactions lead to measurable energy changes, underpinning the mechanics of both natural and engineered systems.
FAQ
Negative work occurs when the force and displacement are in opposite directions. This means energy is transferred from the object to another system, rather than into it.
For example, when a car brakes, frictional forces act opposite to motion. These forces do negative work, removing kinetic energy from the car and converting it into heat and sound.
Negative work is not “less useful work” — it simply represents an energy transfer out of the system.
No. While work is a major pathway for energy transfer, it’s not the only one.
Mechanical systems can also transfer energy through:
Heating (e.g., friction increasing internal energy)
Radiation (though minimal in most mechanical contexts)
Work specifically involves a force causing displacement. Heating or radiation may occur without mechanical movement, so not all energy transfers are classed as work.
If a force acts at 90° to the direction of motion, the cos θ term in W = F s cos θ becomes zero.
This means no component of the force acts along the displacement — so no energy is transferred.
A classic example is uniform circular motion: the centripetal force is always perpendicular to velocity, so it changes direction but not speed, resulting in zero work done.
For non-contact forces such as gravity, the equivalence still holds — energy is transferred through the field rather than by direct physical contact.
When a mass falls, gravitational potential energy decreases and an equal amount of kinetic energy increases. The gravitational field performs work on the object, transferring energy without any contact between the masses.
This demonstrates that fields can mediate energy transfer via work, consistent with the same mechanical principles.
Work can increase internal energy when forces cause deformation, friction, or compression, rather than net movement.
Examples include:
Frictional work converting mechanical energy into heat.
Compressing a gas, where work done increases internal energy and temperature.
Stretching a material beyond its elastic limit, where work alters internal structure.
In each case, work is still done — but the energy transfer changes microscopic motion (internal energy) rather than macroscopic kinetic or potential energy.
Practice Questions
Question 1 (2 marks)
A student pushes a trolley along a smooth horizontal surface using a constant force of 20 N over a distance of 3.0 m.
(a) Calculate the work done on the trolley by the student.
(b) State the energy transfer that occurs as a result of this work.
Mark scheme:
(a) W = F × s = 20 × 3.0 = 60 J (1 mark)
(b) The trolley gains kinetic energy (1 mark)
Question 2 (5 marks)
A piston compresses a gas inside a closed cylinder. The piston is pushed inwards with a constant force of 500 N over a distance of 0.10 m.
(a) Calculate the work done on the gas.
(b) Explain, in terms of energy transfer, what happens to the gas as it is compressed.
(c) The gas then expands and does 40 J of work on the piston. Using your answers, explain how the principle of equivalence between work done and energy transfer applies to this situation.
Mark scheme:
(a) W = F × s = 500 × 0.10 = 50 J (1 mark)
(b) The gas gains energy as work is done on it; this energy increases its internal energy and possibly its temperature (1 mark for energy transfer to gas, 1 mark for correct energy form)
(c) The energy transferred to the gas (50 J) equals the work done on it, showing energy in = work done (1 mark).
When the gas expands, it does work (40 J) on the surroundings, transferring energy out of the system (1 mark).
The difference between input and output energy remains in the system as internal energy (1 mark).

