OCR Specification focus:
‘Derive and apply P = Fv for constant force at steady speed along the line of motion.’
Mechanical power connects force and motion, describing how quickly work is done when an object moves under a constant force. It underpins the analysis of energy transfer and performance in physical systems.
Understanding Mechanical Power
In mechanics, power measures the rate at which work is done or energy is transferred. While work quantifies the total energy transferred, power expresses how fast this transfer occurs. For example, a car engine providing the same total energy over a shorter time interval produces higher power.
Power: The rate of doing work or energy transfer per unit time.
In the context of mechanical systems, power links the applied force and the resulting velocity of motion. This relationship becomes particularly clear when both the force and the speed remain constant along the same line of motion.
Deriving the Equation P = Fv
To understand how force and velocity determine mechanical power, begin with the general definition of power:
EQUATION
—-----------------------------------------------------------------
Power (P) = Work done (W) ÷ Time (t)
P = W / t
W = Work done, measured in joules (J)
t = Time, measured in seconds (s)
—-----------------------------------------------------------------
Work done by a constant force acting along a displacement sss is given by W=FscosθW = F s \cos \thetaW=Fscosθ, where θ\thetaθ is the angle between the force and direction of motion. Substituting into the expression for power gives:
EQUATION
—-----------------------------------------------------------------
Mechanical Power (P) = F s cosθ ÷ t
Since speed (v) = s ÷ t, then
P = Fv cosθ
—-----------------------------------------------------------------
This equation shows that mechanical power equals the product of the force, velocity, and the cosine of the angle between them.
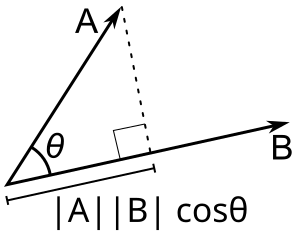
Dot product geometry: the power relation P=FvcosθP = Fv\cos\thetaP=Fvcosθ arises because only the component of force parallel to velocity does work per unit time. The diagram illustrates a vector’s projection onto another, matching the cosine factor in your formula. Note: the figure is a general vector diagram; its mathematical labels go slightly beyond the syllabus, but the geometric idea is exactly what P=FvcosθP = Fv\cos\thetaP=Fvcosθ uses. Source.
When the force and velocity are in the same direction (θ=0°\theta = 0°θ=0°), cosθ = 1, and the formula simplifies to:
EQUATION
—-----------------------------------------------------------------
Mechanical Power (P) = Fv
F = Constant force, measured in newtons (N)
v = Constant velocity, measured in metres per second (m s⁻¹)
P = Power, measured in watts (W)
—-----------------------------------------------------------------
The watt (W) is the SI unit of power, equivalent to one joule of energy transferred per second.
Between equations, it is useful to note that this simplified form, P = Fv, applies only for motion along a straight line at steady speed. When motion involves changing direction or acceleration, this linear relationship no longer holds, and instantaneous power must be considered.
Applying the Equation in Context
The equation P = Fv is fundamental in mechanical and engineering contexts where forces cause steady motion. For instance:
In motors and engines, it quantifies how much useful mechanical power is produced to overcome friction and resistive forces.
In transport systems, it determines the power required to maintain constant speed against drag or slope resistance.
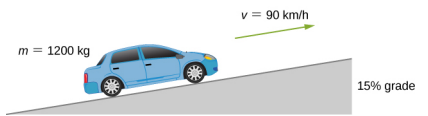
Power at steady speed on a slope: to keep speed constant, the engine supplies power at a rate equal to the component of weight (and other resistive forces) times velocity. For a uniform incline, the gravitational contribution is mgsinθmg\sin\thetamgsinθ, giving P=mgvsinθP = mgv\sin\thetaP=mgvsinθ when other losses are neglected, which is a direct application of P=FvP = FvP=Fv. The figure also mentions air resistance; that extra detail is not required by the syllabus but does not affect the core P=FvP = FvP=Fv idea. Source.
In lifting machines, it measures the rate at which energy is transferred to raise a load at a uniform velocity.
In all these examples, force represents the component of the total applied force that acts in the direction of motion. If motion occurs at an angle or under multiple forces, only the parallel component contributes to useful power.
Direction and Significance of Power
When analysing mechanical power, the direction of motion relative to the applied force determines whether power is positive or negative:
Positive power occurs when the force acts in the same direction as the motion, meaning energy is transferred to the object.
Negative power arises when the force acts opposite to the motion, such as friction or braking, meaning energy is taken from the object.
This sign convention mirrors that used for work done, maintaining consistency in the interpretation of energy transfer in mechanics.
Instantaneous and Average Power
Although P = Fv typically refers to steady motion, it can also describe instantaneous power, representing the power at a particular moment. If either force or velocity varies with time, instantaneous power is determined by multiplying the instantaneous values of force and velocity.
Instantaneous Power: The power at a specific instant, equal to the product of instantaneous force and velocity.
In contrast, average power over a time interval is found by dividing the total work done by the total time taken. This distinction becomes important in systems with variable forces, such as oscillating engines or changing resistance forces in fluids.
Relationship to Energy Transfer and Efficiency
Mechanical power provides a direct link between force, motion, and energy transfer. Since work done = energy transferred, the rate of energy transfer per second is the same as mechanical power. This forms the basis for defining mechanical efficiency, as real systems rarely convert all input energy into useful output.
A high-power system can transfer energy quickly, but this does not guarantee efficiency.
Some of the power may be dissipated as heat or sound, reducing the useful output.
Engineers use P = Fv to estimate required power outputs and energy demands for steady operations.
Factors Affecting Mechanical Power Output
Several factors determine the mechanical power produced or absorbed by a system:
Magnitude of the applied force: Greater force increases power if speed is constant.
Velocity of motion: Faster motion under the same force also increases power.
Angle between force and velocity: Only the component parallel to motion contributes to power; a perpendicular force produces zero power.
Resistive forces: Friction, drag, or weight components opposing motion reduce the net useful power output.
Understanding these relationships allows physicists to evaluate the energy performance of machines, transport systems, and industrial processes, ensuring they operate within design limits and safety standards.
Conceptual Interpretation
The equation P = Fv highlights that mechanical power represents the rate of energy conversion from one form to another. When a motor exerts a steady force on a moving conveyor belt, electrical energy is converted into mechanical work at a rate determined by both the force applied and the speed of the belt. Likewise, when a resisting force acts on a moving object, mechanical power quantifies the rate of energy dissipation.
In essence, mechanical power from force and speed provides a bridge between the abstract concept of energy transfer and its measurable physical consequences — motion, resistance, and performance — forming a crucial foundation for understanding work, energy, and power in classical mechanics.
FAQ
Useful mechanical power refers to the portion of total power that produces the desired motion or output — for example, driving a vehicle forward or lifting a load.
Total mechanical power includes all the power produced by a source, including energy lost to non-useful forms such as heat, sound, or vibration.
Efficiency can be expressed as:
Useful power output ÷ Total power input × 100%
Losses mean that useful power is always less than total power, even in steady motion at constant velocity.
At constant speed, the net force on an object is zero, but resistive forces (such as friction or drag) still oppose motion.
The applied force equals the resistive force, so work is done every second to overcome these losses. Since both the force and velocity remain constant, their product (P = Fv) also remains constant — giving a steady rate of energy transfer to maintain motion.
Yes. Negative power occurs when the force and velocity vectors are in opposite directions.
This situation arises when:
A braking force slows a moving vehicle.
Friction or air resistance removes kinetic energy.
Negative power means energy is being transferred from the moving object to its surroundings, often as heat, rather than being supplied to sustain motion.
For circular motion, the velocity continually changes direction while the speed remains constant.
If the force is always perpendicular to the motion (as in uniform circular motion), the angle between force and velocity is 90°, so cos 90° = 0, and the mechanical power P = Fv cosθ = 0.
This means the force does no work — it only changes the direction of motion, not the energy of the object.
Mechanical power can be measured by determining both the force applied and the corresponding speed of motion.
Common methods include:
Using a force sensor and motion sensor to measure F and v in real time, then calculating P = Fv.
Measuring the rate of change of work by recording the time taken for a known energy transfer.
In rotational systems, using torque and angular velocity with P = τω, which is the rotational equivalent of P = Fv.
Practice Questions
Question 1 (2 marks)
A car moves at a constant speed of 20 m s⁻¹ along a straight, level road. The total resistive force acting on the car is 1.2 × 10³ N.
Calculate the mechanical power output of the car’s engine needed to maintain this steady speed.
Mark scheme:
Correct use of formula P = Fv (1 mark)
Substitution and correct calculation: P = 1.2 × 10³ × 20 = 2.4 × 10⁴ W (24 kW) (1 mark)
Question 2 (5 marks)
A cable car of total mass 1800 kg moves up a straight incline of angle 15° to the horizontal at a constant speed of 5.0 m s⁻¹. The frictional force opposing its motion is 2.5 × 10³ N.
(a) Calculate the total driving force needed to maintain constant speed. (2 marks)
(b) Determine the power output of the cable car’s motor under these conditions. (2 marks)
(c) State and explain what would happen to the motor power if the car travelled at twice this speed, assuming all other factors remain constant. (1 mark)
Mark scheme:
(a)
Identification of forces: component of weight down slope mg sin θ (1 mark)
Total driving force F = mg sin θ + friction = (1800 × 9.8 × sin15°) + 2.5 × 10³ ≈ 7.1 × 10³ N (1 mark)
(b)
Correct use of formula P = Fv (1 mark)
Substitution and correct calculation: P = 7.1 × 10³ × 5.0 = 3.6 × 10⁴ W (36 kW) (1 mark)
(c)
Recognition that P ∝ v for constant F (1 mark)
Therefore, doubling the speed doubles the required power output, as the rate of doing work increases linearly with velocity.

