OCR Specification focus:
‘Calculate efficiency = useful output ÷ total input × 100%; discuss energy losses in systems.’
Efficiency measures how effectively energy or power is converted from one form to another. Understanding and calculating efficiency helps identify energy losses and improve system performance.
Understanding Efficiency
Efficiency is a key concept in physics that describes how much of the input energy or power supplied to a system is converted into useful output energy or power. In any real process, some energy is inevitably lost to the surroundings, usually as heat, sound, or light. Efficiency provides a quantitative measure of how well a device or process minimises these losses.
The Meaning of Efficiency
The efficiency of a system expresses the proportion of total energy that is usefully transformed, often written as a percentage. It indicates how well energy conversion or transmission occurs within a physical system.
Efficiency: The ratio of useful output energy (or power) to the total input energy (or power), often expressed as a percentage.
An efficient device converts most of the supplied energy into a useful form, while an inefficient one wastes much of it as non-useful forms.
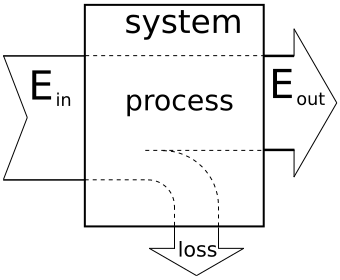
A concise efficiency diagram showing energy in, useful energy out, and losses. The arrows emphasise that not all input becomes useful output, so efficiency is always less than 100% in real systems. This directly supports calculations using efficiency = useful ÷ input × 100%. Source.
Calculating Efficiency
Efficiency can be calculated using energy or power, depending on whether the quantities measured relate to total energy transferred over time or instantaneous power transfer.
EQUATION
—-----------------------------------------------------------------
Efficiency (%) = (Useful Output ÷ Total Input) × 100
Useful Output = Energy or Power output that performs the intended task (joules or watts)
Total Input = Total Energy or Power supplied to the system (joules or watts)
—-----------------------------------------------------------------
When using power, the equation gives an immediate measure of how efficiently a device converts power at a given rate. When using energy, the calculation reflects efficiency over a complete process or time period.
A perfectly efficient system would have 100% efficiency, meaning all input energy becomes useful output. However, due to unavoidable energy losses, real systems always have efficiency values below 100%.
Example Contexts
Though not calculated here, efficiency applies to:
Electric motors converting electrical energy to kinetic energy.
Light bulbs converting electrical energy to light, with heat as a by-product.
Engines converting chemical energy from fuel into mechanical work.
In each case, part of the input energy dissipates as thermal or sound energy, reducing efficiency.
Interpreting Efficiency Values
Efficiency values are always dimensionless, often expressed either as a decimal fraction (e.g. 0.85) or as a percentage (e.g. 85%).
High efficiency (close to 1 or 100%) means minimal losses.
Low efficiency (well below 1 or 100%) indicates significant wasted energy.
When comparing devices or systems, engineers and physicists use efficiency to determine which option best conserves energy resources.
Energy Conservation in Efficiency
Although efficiency expresses energy losses, it aligns with the principle of conservation of energy, which states that energy cannot be created or destroyed, only transferred or transformed. Energy lost from a system’s useful output is not destroyed; it is transferred to less useful stores such as the thermal energy store of the surroundings.
Sources and Types of Energy Loss
No real system is perfectly efficient because some energy is inevitably dissipated. Common sources of inefficiency include:
Friction: Converts kinetic energy into thermal energy, heating the surroundings.
Electrical resistance: Converts electrical energy into heat in conductors.
Air resistance: Converts mechanical energy into heat through drag.
Sound production: Unwanted vibration energy radiated as sound waves.
Incomplete energy transfer: Some input energy fails to reach the intended component.
These losses often appear as waste energy, which still obeys conservation laws but serves no useful purpose.
Reducing Energy Losses
Improving efficiency involves minimising unwanted energy transfers. Strategies include:
Lubrication to reduce friction between moving parts.
Streamlined designs to lower air resistance.
Thermal insulation to limit heat loss in systems.
High-conductivity materials to reduce electrical losses.
Maintenance and calibration to ensure machines operate optimally.
By addressing energy loss mechanisms, engineers can raise efficiency and reduce energy costs.
Efficiency in Power and Energy Contexts
In mechanical and electrical systems, the relationship between power and efficiency is particularly important.
EQUATION
—-----------------------------------------------------------------
Efficiency = Useful Power Output ÷ Total Power Input
Useful Power Output = Rate at which useful energy is transferred (watts)
Total Power Input = Rate at which energy is supplied to the system (watts)
—-----------------------------------------------------------------
In practice, power-based efficiency calculations are common in devices like motors, engines, and generators, where energy transfers occur continuously over time.
A lower efficiency indicates that more input power is needed to achieve the same useful effect, which increases both energy consumption and operational costs.
Linking Power and Energy Efficiency
Because power is the rate of energy transfer, the efficiency formula using power is equivalent to that using energy. The choice of which to use depends on the data available. Engineers typically prefer power-based efficiency for continuously operating devices, while energy-based efficiency suits processes that occur once or over a defined duration.
Interpreting Efficiency in Real Devices
Manufacturers often specify efficiency ratings to indicate expected performance.
A simplified EU energy efficiency label, illustrating how devices are graded to indicate relative efficiency. Such ratings help users compare useful output per unit input across similar products. Extra detail: the full EU labelling scheme spans several classes and icons beyond what OCR requires. Source.
These ratings help consumers and engineers assess cost-effectiveness and environmental impact. For instance:
Electrical appliances display efficiency ratings to show energy consumption relative to output performance.
Engines and turbines are evaluated for fuel efficiency to reduce emissions and operating costs.
Renewable energy systems such as solar panels list conversion efficiency to express how much incident sunlight is converted to electrical energy.
These interpretations allow practical comparison between technologies performing the same function.
Efficiency and Energy Costs
The efficiency of a device influences the cost of operation. Inefficient devices require more energy input for the same useful output, leading to higher running expenses. Energy companies and consumers alike aim to use more efficient equipment to save both energy and money while reducing environmental impact.
Improving efficiency therefore supports sustainability and resource conservation—core aims of modern physics applications in energy systems.
FAQ
In practice, several unavoidable effects reduce efficiency compared to ideal conditions.
Friction and drag: These convert useful mechanical energy into heat.
Electrical resistance: Conductors generate waste heat as current flows.
Thermal losses: Energy escapes through conduction, convection, or radiation.
Imperfect energy transfer: Some input energy never reaches the intended component.
Even with precise design, material limitations and environmental factors such as temperature and air resistance ensure that 100% efficiency is never achieved.
This occurs due to measurement errors rather than true over-performance.
Possible causes include:
Inaccurate readings of power input or output, especially if meters are miscalibrated.
Neglecting losses such as friction, causing underestimated input values.
Rounding errors or inconsistent time measurements in energy calculations.
Correcting for measurement uncertainty and improving experimental control usually brings calculated efficiencies back below 100%.
In electrical systems, energy losses primarily appear as heat in wires, resistors, and motors due to electrical resistance.
In mechanical systems, losses arise from friction, air resistance, and sound production.
While both involve energy dissipation to the surroundings, electrical losses are often localised within circuits, whereas mechanical losses may spread across multiple components or through vibration.
Percentage efficiency offers greater clarity and ease of comparison between systems.
For example, expressing efficiency as 80% immediately conveys that 20% of input energy is wasted, which is more intuitive than writing 0.8.
However, engineers and physicists often use decimal efficiency in calculations because it avoids extra conversion steps and is better suited to computational work or modelling.
Rising temperature generally reduces efficiency.
In electrical devices, increased temperature raises resistance in wires, meaning more energy is lost as heat.
In engines or motors, higher temperatures may lead to thermal expansion, increasing friction or altering material performance.
Maintaining an optimal operating temperature through cooling systems or heat sinks helps minimise energy losses and sustain efficiency over time.
Practice Questions
Question 1 (2 marks)
Define efficiency and state how it can be expressed mathematically.
Mark Scheme:
1 mark for correctly defining efficiency as the ratio of useful output energy (or power) to total input energy (or power).
1 mark for giving the correct formula: efficiency = (useful output ÷ total input) × 100%.
Question 2 (5 marks)
An electric motor has an input power of 600 W and a useful mechanical power output of 480 W.
(a) Calculate the efficiency of the motor. (2 marks)
(b) Explain what this efficiency value indicates about the motor’s performance and identify two ways its efficiency could be improved. (3 marks)
Mark Scheme:
(a)
1 mark for using the correct formula: efficiency = (useful output ÷ total input) × 100%.
1 mark for obtaining the correct numerical value: (480 ÷ 600) × 100 = 80%.
(b)
1 mark for recognising that an efficiency of 80% means 20% of the input power is wasted or lost (e.g., as heat or sound).
1 mark for identifying one method of improvement, such as reducing friction by lubrication or using better bearings.
1 mark for identifying a second valid improvement method, such as using more efficient electrical conductors to reduce resistance losses or improving thermal insulation.

