OCR Specification focus:
‘Define power as rate of doing work, P = W ÷ t; use the watt as the SI unit.’
Power measures how quickly work is done or energy is transferred in physical processes. Understanding power connects force, energy, and time — vital for analysing mechanical systems.
Understanding Power
Power is a fundamental physical quantity that expresses how rapidly energy is converted from one form to another or how quickly work is performed. In physics, it provides insight into the rate of energy transfer rather than the total energy involved. This distinction makes it essential for comparing systems that perform the same amount of work but at different speeds, such as engines, motors, or even the human body.
The Concept of Work and Energy Transfer
Before defining power formally, it is important to recall what work represents. Work quantifies the energy transferred when a force acts through a displacement. When work is done, energy leaves one system and enters another. For instance, when a person lifts a box, chemical energy from muscles is transferred into gravitational potential energy of the box.
The rate at which this transfer occurs determines the power. If the same amount of work is done more quickly, more power is produced. This rate-based relationship underpins the definition of power.
Definition of Power
Power: The rate at which work is done or energy is transferred.
This definition emphasises that power concerns the rate of energy change, measured over time. The faster the energy transfer, the higher the power.
Mathematical Expression for Power
EQUATION
—-----------------------------------------------------------------
Power (P) = Work done (W) ÷ Time taken (t)
P = W ÷ t
P = rate of doing work
W = work done (joules, J)
t = time taken (seconds, s)
—-----------------------------------------------------------------
This equation shows that power depends on both the amount of work done and the duration of that work. If a machine performs 100 joules of work in one second, it delivers 100 watts of power. If it takes two seconds, the power output halves.
The Watt as the SI Unit
Watt (W): The SI unit of power, equivalent to one joule of work done per second.
Hence, 1 W = 1 J s⁻¹. The watt measures how much energy is converted or transferred per second. Larger power outputs are often expressed in kilowatts (kW) or megawatts (MW), particularly for engines, power stations, or industrial applications.

An analogue wattmeter used to measure the rate of energy transfer in electric circuits, displayed in watts (W). The moving-coil needle indicates instantaneous power under steady conditions. This image aligns with defining power as the rate of doing work and highlights the watt as the SI unit. Source.
Between any two systems, the power output or input can describe performance efficiency and energy usage. For example, a 60 W light bulb converts 60 joules of electrical energy into light and heat every second.
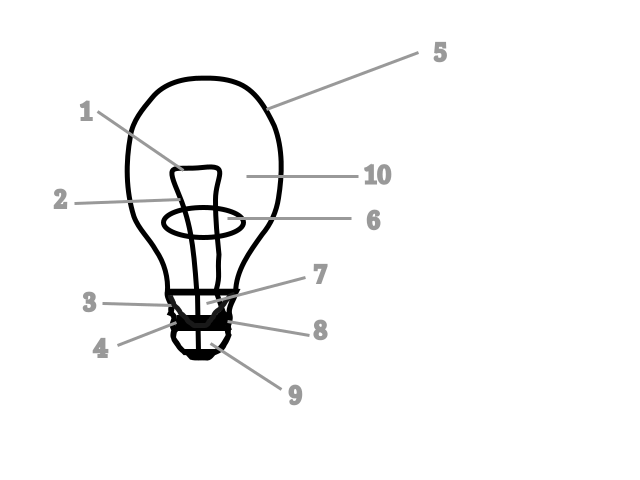
Diagram of an incandescent bulb showing its principal components. In practice, manufacturers print a power rating (e.g. 60 W) on the bulb or base to indicate the rate of energy conversion. The diagram itself focuses on structure; it does not show the printed rating — this is extra contextual detail beyond the labeled parts. Source.
The Physical Interpretation of Power
Power as Rate of Work
Power provides an instantaneous measure of how efficiently a system performs mechanical tasks. If a force remains constant and acts in the direction of motion, the rate of energy transfer stays constant. In contrast, when the force or motion changes over time, the instantaneous power can vary continuously.
Constant vs. Variable Power
Constant Power: Occurs when work is done at a steady rate, such as a motor lifting a load at uniform speed.
Variable Power: Appears when either the force or speed changes, such as a car accelerating from rest.
When power varies, it can be described as the instantaneous power, which is the derivative of work or energy with respect to time.
EQUATION
—-----------------------------------------------------------------
Instantaneous Power (P) = dW/dt
P = rate of change of work done with time
—-----------------------------------------------------------------
This expression extends the basic definition of power to cases where energy transfer is non-uniform, enabling analysis of dynamic systems like engines, turbines, or oscillating masses.
Relationship Between Power, Force, and Motion
Although this subsubtopic focuses on defining power, understanding its link to force and velocity reinforces the physical meaning. When a constant force acts on an object moving with constant velocity, the work done per unit time gives another useful expression for power.
EQUATION
—-----------------------------------------------------------------
Power (P) = Force (F) × Velocity (v)
F = applied force (newton, N)
v = velocity (metres per second, m s⁻¹)
—-----------------------------------------------------------------
This equation shows that mechanical power depends on both the magnitude of the force and the speed of motion along the direction of that force. It highlights why increasing speed or force increases power output, provided the other quantity remains constant.
Practical Understanding of Power
Comparing Energy and Power
While energy measures the total work done or potential for doing work, power determines how fast that energy is delivered. A small engine may perform the same total work as a large one, but if it takes longer, its power rating is lower. This explains why devices with higher power ratings can complete tasks more quickly.
For instance:
A high-power electric motor can lift a heavy load faster than a low-power motor.
A 1000 W kettle boils water more quickly than a 750 W kettle, transferring heat energy at a greater rate.
Power in Different Physical Contexts
Power is not confined to mechanical systems. It is relevant across all energy transformations:
Electrical Power: Measures the rate of electrical energy transfer (e.g. P = VI).
Thermal Power: Describes heat transfer rates in heaters or radiators.
Radiative Power: Quantifies energy emitted per second by a source, such as the Sun or a light bulb.
Each of these shares the same core definition — the rate of energy transfer — but the form of energy varies with the system.
Power Ratings in Real Devices
Manufacturers specify power ratings to indicate how rapidly a device uses or outputs energy. The rating helps users predict performance and energy consumption. For example:
A 60 W bulb converts electrical energy at a rate of 60 joules per second.
A 2 kW hairdryer transfers 2000 joules of energy each second from electricity to thermal and kinetic energy.
Such ratings are vital in practical energy management, ensuring electrical circuits are designed safely and efficiently.
The Broader Significance of Power
The concept of power links closely to efficiency and energy conservation principles. In any real system, not all input energy becomes useful output; some is lost as heat, sound, or vibration. By measuring power input and output, the efficiency of energy conversion can be determined — a topic explored in later subsubtopics.
Ultimately, defining power as the rate of doing work enables quantitative assessment of how quickly physical, electrical, or chemical processes occur, forming a foundation for engineering design, performance comparison, and sustainable energy use.
FAQ
Average power is calculated over a measurable time interval, representing the total work done divided by total time. It provides a general indication of performance but ignores fluctuations during that period.
Instantaneous power, on the other hand, is the power at a specific moment in time. It is given by the rate of change of work or energy with respect to time (P = dW/dt). This form is useful for systems where force or speed changes continuously, such as engines or oscillating systems.
Power is a scalar because it describes the rate of energy transfer, which has magnitude but no direction.
Although force and velocity are both vectors, power depends on their scalar product (dot product). The scalar product produces a single numerical value representing how much of the force contributes to motion in the same direction. This means power can be positive, negative, or zero, but it cannot have a direction.
Negative power indicates that energy is being transferred from a system rather than to it.
Examples include:
A moving object being slowed by friction, where the resistive force does negative work.
A generator converting mechanical work into electrical energy — the system is losing energy as it performs work on another system.
In contrast, positive power signifies energy input, such as a motor supplying mechanical energy.
Efficiency compares useful power output with total power input.
If a machine has high efficiency, most of the input energy is converted into useful work rather than wasted as heat, sound, or vibration. Conversely, low efficiency means a larger proportion of the input power is lost to the surroundings.
Efficiency (%) = (useful power output ÷ total power input) × 100
Real-world systems rarely achieve 100% efficiency due to unavoidable energy losses.
While energy indicates the total work a system can perform, power shows how quickly that energy is used or delivered.
Two machines may transfer the same total energy, but if one does so in half the time, it has twice the power. This makes power the preferred quantity when assessing performance, response speed, or suitability for time-sensitive applications — for instance, comparing electric motors, generators, or household appliances.
Practice Questions
Question 1 (2 marks)
Define power and state its SI unit.
Mark scheme:
1 mark: Correctly defines power as the rate of doing work or the rate of energy transfer.
1 mark: States the SI unit of power as the watt (W).
Question 2 (5 marks)
A motor lifts a 50 kg load vertically through a height of 4.0 m in 5.0 s.
(a) Calculate the work done by the motor.
(b) Calculate the average power output of the motor.
(c) Explain what the calculated power value represents and how it would change if the same load were lifted in half the time.
Mark scheme:
(a) 1 mark: Correctly identifies formula for work done: W = m g h.
Substitution: W = 50 × 9.8 × 4.0 = 1960 J → 1 mark.
(b) 1 mark: Uses power equation P = W ÷ t.
Substitution: P = 1960 ÷ 5.0 = 392 W → 1 mark.
(c) 1 mark: Explains that power represents the rate of doing work or transferring energy by the motor.
1 mark: States that if the same load were lifted in half the time, the power would double because the same work is done in less time.

