OCR Specification focus:
‘Kirchhoff’s first law: at a junction, total current in equals total current out.’
Understanding Kirchhoff’s First Law
Electric circuits often involve multiple branches where electric current divides or recombines. Kirchhoff’s First Law provides a fundamental principle describing how current behaves at such points. It ensures that electrical charge is neither created nor destroyed within a circuit but simply redistributed among different paths. This principle forms the foundation of circuit analysis, underpinning all calculations involving current flow through networks of resistors, power supplies, and components.
Kirchhoff’s First Law, sometimes called the current law or junction rule, expresses the concept of conservation of charge in electrical systems — a key physical law derived from the invariance of electric charge in all processes.
The Principle of Conservation of Charge
The principle of conservation of charge states that the total electric charge in an isolated system remains constant over time. Electric charge cannot be created or destroyed, only transferred. In the context of circuits, this means that the amount of charge entering a point must equal the amount leaving it, ensuring balance and continuity of current.
Conservation of Charge: The total electric charge in an isolated system is constant; charge can move between bodies but is never lost or created.
Because charge carriers (such as electrons) cannot simply vanish, any charge flowing into a junction must flow out along other branches. This forms the physical basis for Kirchhoff’s First Law.
Kirchhoff’s First Law Explained
Kirchhoff’s First Law: At any junction in an electrical circuit, the total current entering the junction equals the total current leaving the junction.
A junction (or node) is a point where three or more conductors meet. Current is the rate of flow of charge, measured in amperes (A), where 1 A = 1 coulomb per second. When multiple paths exist, the current divides so that the total inflow equals the total outflow.
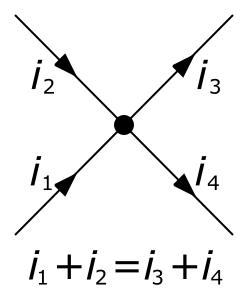
Diagram of a junction illustrating Kirchhoff’s first law: the total current entering equals the total current leaving. Currents i₁ and i₂ flow into the node, while i₃ and i₄ leave, so i₁ + i₂ = i₃ + i₄. The layout is minimal and directly supports charge conservation at a node. Source.
For example, if two currents of 3 A and 2 A enter a junction, the combined 5 A must leave through the outgoing branches. This is a direct consequence of conservation of charge: the charge per second flowing into the point equals that leaving.
Mathematical Expression of Kirchhoff’s First Law
EQUATION
—-----------------------------------------------------------------
Kirchhoff’s First Law (ΣI = 0)
ΣI = Sum of currents entering and leaving a junction
I = Current in a branch (A)
Positive I = Current entering the junction
Negative I = Current leaving the junction
—-----------------------------------------------------------------
When currents entering a junction are taken as positive and currents leaving as negative (or vice versa), their algebraic sum is always zero. This equation is commonly written as ΣI = 0, expressing current balance.
Relation to Charge Flow
Since current (I) is the rate of flow of charge (Q) through a point per unit time (t), Kirchhoff’s First Law follows directly from the definition of current.
EQUATION
—-----------------------------------------------------------------
Current (I) = Q ÷ t
Q = Charge (C)
t = Time (s)
—-----------------------------------------------------------------
At a junction, the total charge entering per second equals the total charge leaving per second. The conservation of charge ensures that no charge accumulates at the junction under steady-state conditions. If this were not true, the junction would gain or lose charge, creating an impossible situation in a typical metallic circuit.
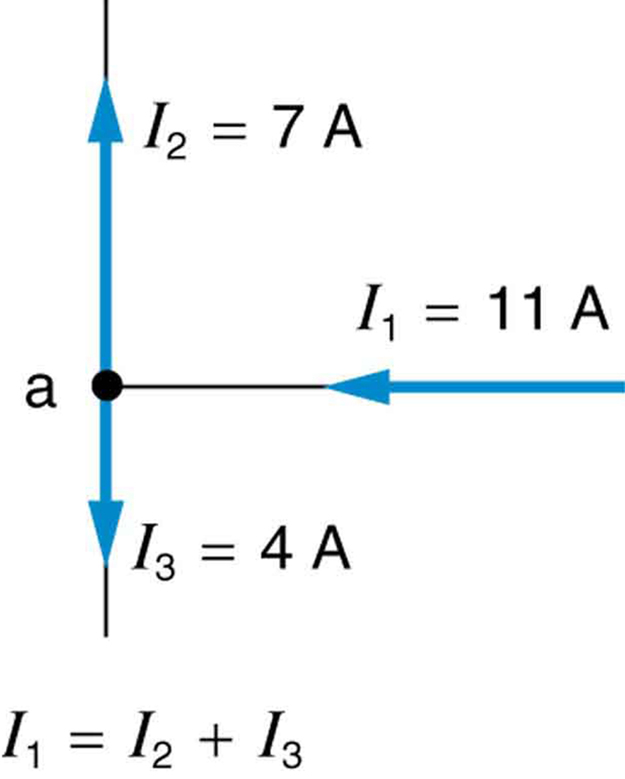
Kirchhoff’s junction rule visualised: a current I₁ entering a T-junction splits into I₂ and I₃ so that I₁ = I₂ + I₃. This directly expresses conservation of charge at a node. The figure is concise and aligned with A-level treatment. Source.
Physical Interpretation at the Microscopic Level
On a microscopic scale, electrical current results from the movement of charge carriers, such as electrons in metals or ions in electrolytes. When these carriers reach a junction, they are redistributed into available paths. Kirchhoff’s First Law states that every electron entering a junction must exit via one of the connected branches; none disappear or are created at the node.
This microscopic interpretation reinforces that charge conservation operates at every level of matter. The junction simply channels the flow, maintaining equilibrium across the network.
Applying the Law in Circuit Analysis
Kirchhoff’s First Law is essential when analysing parallel circuits and complex networks where current splits or combines. It provides a systematic way to calculate unknown currents when multiple components are connected.
When applying the law:
Identify all junctions in the circuit diagram.
Assign a direction to each branch current (the assumed positive direction).
Apply Kirchhoff’s First Law at each junction by writing an equation where the sum of currents entering equals the sum of currents leaving.
Solve the resulting simultaneous equations to find unknown currents.
The accuracy of this process relies entirely on the conservation of charge principle.
Significance in Electrical Systems
Kirchhoff’s First Law underpins the analysis of all electrical networks, from simple circuits to large-scale power grids. Its importance extends beyond theory into practical engineering applications, including:
Design of electrical distribution systems where current balance prevents overloads.
Testing of circuits to ensure proper wiring and current continuity
Verification of measurements, since inconsistent current readings may indicate component faults or connection errors.
In each application, the law ensures that electrical systems behave predictably according to charge conservation.
Limitations and Conditions
Kirchhoff’s First Law assumes that:
The circuit operates under steady-state conditions, meaning charge does not accumulate at any point.
The conductors are perfect, with negligible charge storage at junctions.
The system is macroscopic, not affected by transient effects such as displacement currents in capacitors or rapidly varying electromagnetic fields.
In high-frequency circuits or where capacitive and inductive effects dominate, displacement current may appear to violate Kirchhoff’s First Law momentarily. However, when extended to include displacement current as part of the total current, the principle of charge conservation remains fully valid.
Conceptual Importance
Kirchhoff’s First Law connects the physical principle of charge conservation to practical circuit behaviour. It provides a direct link between microscopic processes — the motion of individual charges — and macroscopic observations, such as measured currents in wires and components. This makes it one of the cornerstones of both classical circuit theory and modern electrical engineering.
By ensuring that all current entering a junction also leaves, Kirchhoff’s First Law guarantees continuity and balance in electrical systems, reflecting the unbreakable conservation of electric charge that governs the behaviour of all matter.
FAQ
Apparent violations often arise from measurement errors rather than genuine breakdowns of the law. Inaccurate ammeter readings, poor connections, or unaccounted current leakage can make it seem as though current is not conserved.
In reality, Kirchhoff’s first law holds true whenever charge is conserved. If discrepancies persist, students should check for:
Faulty or incorrectly connected ammeters
Internal resistance within meters or wires
Parallel paths through the measuring equipment
Yes — Kirchhoff’s first law still applies to AC circuits because charge conservation remains valid. At every instant, the instantaneous current entering a junction equals the instantaneous current leaving.
However, since AC current changes direction periodically, the current values are often expressed as r.m.s. (root mean square) values rather than instantaneous ones when performing practical calculations.
It can, but care is needed. During transient processes, such as when a capacitor is charging or discharging, the displacement current in the electric field must be included in the total current balance.
If displacement current is considered, the law remains valid even though conventional current in the wires is changing. Ignoring this can lead to apparent violations in high-frequency or time-varying systems.
In nodal analysis, Kirchhoff’s first law is applied systematically to every node in a circuit to set up simultaneous equations.
The process typically involves:
Assigning a potential to each node
Expressing each branch current using Ohm’s law
Applying Kirchhoff’s first law to each node (sum of currents = 0)
Solving the resulting equations yields the unknown potentials and currents throughout the circuit.
Under steady-state conditions, the amount of charge at any junction remains constant with time. This allows the assumption that current in equals current out.
If charge were to build up (as in a capacitor or during switching), the current balance momentarily changes. The law still fundamentally holds but must include the time rate of change of stored charge to remain accurate.
Practice Questions
Question 1 (2 marks)
At a junction in a circuit, a current of 3.0 A enters and two currents of 1.2 A and 1.8 A leave.
Explain, using Kirchhoff’s first law, whether charge is conserved at this junction.
Mark Scheme:
1 mark: States Kirchhoff’s first law – the total current entering a junction equals the total current leaving it.
1 mark: Correctly shows that 3.0 A entering equals 1.2 A + 1.8 A leaving, confirming that charge is conserved at the junction.
Question 2 (5 marks)
A circuit has three branches meeting at a single junction. The currents in two of the branches are measured as follows:
• 2.5 A flows into the junction from branch X
• 1.8 A flows out of the junction through branch Y
(a) Using Kirchhoff’s first law, calculate the current in the third branch (Z), stating its direction relative to the junction. (2 marks)
(b) Explain how Kirchhoff’s first law is a consequence of the principle of conservation of charge. (3 marks)
Mark Scheme:
(a)
1 mark: Correct application of Kirchhoff’s first law: total current entering = total current leaving.
1 mark: Correct calculation and direction – 0.7 A must leave the junction through branch Z.
(b)
1 mark: States that charge cannot be created or destroyed, only transferred.
1 mark: Explains that the total charge flowing into a junction per second equals the total charge flowing out per second.
1 mark: Links this to Kirchhoff’s first law by noting that equal charge flow per second means equal current, so current in equals current out.

