OCR Specification focus:
‘Mean drift velocity describes average motion of charge carriers through a conductor.’
Electric current in conductors arises from the collective motion of countless microscopic charge carriers. The mean drift velocity concept connects this microscopic behaviour to observable macroscopic current.
The Concept of Charge Carriers
Understanding Charge Carriers
In all materials that conduct electricity, charge carriers are the particles responsible for transporting electric charge through the substance. These carriers differ between types of materials:
In metals, the charge carriers are free electrons detached from their parent atoms within the metallic lattice.
In electrolytes, ions act as the charge carriers, moving in opposite directions according to their charge.
In semiconductors, electrons and holes both serve as charge carriers depending on the type of doping.
Charge Carrier: A particle, such as an electron or ion, that carries electric charge and is free to move through a material under the influence of an electric field.
The motion of charge carriers underpins the flow of electric current, linking the microscopic world of atomic-scale motion with the macroscopic electrical quantities measured in circuits.
Linking Microscopic Motion to Macroscopic Current
Random Thermal Motion and Net Drift
Even in the absence of an electric field, free electrons in a conductor move rapidly and randomly due to thermal energy. However, these random motions average out to no net current because movement in all directions cancels overall charge transport.
When a potential difference is applied across the conductor, an electric field is established. This field exerts a force on each charge carrier, causing them to accelerate opposite to the field direction if they are negatively charged (like electrons), or along it if they are positively charged (like positive ions). The electrons experience frequent collisions with fixed ions in the lattice, resulting in a slow average drift velocity superimposed on their random motion.
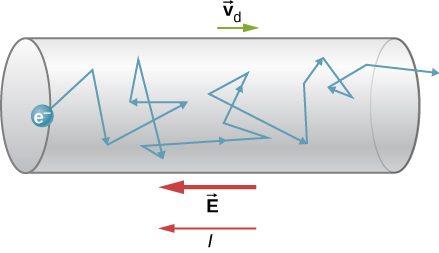
Schematic showing a single electron’s zig-zag path through a conductor, with collisions and a small drift velocity opposite to the electric field. The diagram highlights that random thermal motion coexists with a net bias, producing current without requiring large particle speeds. Labels are clean and minimal, matching the conceptual level required. Source.
Mean Drift Velocity: The average velocity of charge carriers moving through a conductor when an electric field is applied, representing the net flow of charge in one direction.
The drift velocity is typically extremely small — often just a few millimetres per second — even though electrical signals propagate through the circuit almost instantaneously due to the rapid establishment of the electric field throughout the conductor.
The Direction of Motion
Conventional Current and Electron Flow
The direction of conventional current is defined as the direction positive charge would flow. In metallic conductors, where electrons are the charge carriers, this means current direction is opposite to the actual motion of electrons. This distinction helps ensure consistent analysis of circuits, even though electrons themselves move in the reverse direction.
Influence of Charge Type
In electrolytes, positive ions (cations) drift toward the negative electrode, while negative ions (anions) drift toward the positive electrode. The combined motion of these oppositely directed charge carriers produces the total electric current through the electrolyte. The same principle applies to semiconductors, where electrons and holes contribute additively to current flow in opposite directions.
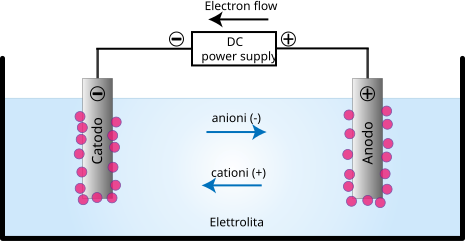
Labeled electrolytic cell showing cations drifting toward the cathode and anions toward the anode, completing the circuit through solution. This image focuses on carrier type and direction rather than reaction details, aligning with the subsubtopic’s scope. Note: the diagram includes electrode labels and a battery symbol; these are minor extras that do not exceed the conceptual requirements. Source.
Quantitative Relationship Between Drift Velocity and Current
While this section focuses on the conceptual understanding, the mean drift velocity forms the basis of the quantitative relationship expressed in the continuity equation, where current is related to charge carrier density, charge, cross-sectional area, and drift velocity. Understanding the concept qualitatively ensures a foundation for applying the equation correctly.
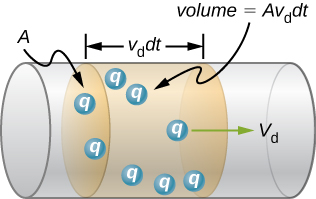
Diagram of a wire showing a shaded slice of thickness vd dtv_d\,dtvddt and cross-section AAA, with charges qqq moving through. It emphasises that current counts the number of carriers crossing an area per second and that drift velocity is typically small. The image includes variables beyond the syllabus narrative but only to label the geometry; no derivation is shown. Source.
EQUATION
—-----------------------------------------------------------------
Electric Current (I) = A n e v
I = Electric current (ampere, A)
A = Cross-sectional area of conductor (square metre, m²)
n = Number density of charge carriers (per cubic metre, m⁻³)
e = Charge of each carrier (coulomb, C)
v = Mean drift velocity (metre per second, m s⁻¹)
—-----------------------------------------------------------------
Although the equation appears in a later subsubtopic, it is directly connected to the concept introduced here. Each variable represents a physical aspect of the microscopic process that together defines observable current.
After introducing an electric field, each charge carrier moves with a net velocity dependent on:
The magnitude of the applied potential difference, which sets the field strength.
The type of material, determining how frequently collisions occur.
The density of charge carriers, as more carriers contribute to a greater total current for the same drift speed.
Factors Affecting Mean Drift Velocity
1. Number Density of Carriers
The number density (n) is the number of charge carriers per unit volume. Materials with high nnn, such as metals, can sustain large currents even with small drift velocities. Conversely, in semiconductors, nnn is much lower, requiring higher drift velocities to produce comparable currents.
2. Cross-sectional Area of the Conductor
A wider conductor allows more charge carriers to flow simultaneously. Hence, for the same current, a larger cross-sectional area means a smaller mean drift velocity is needed.
3. Electric Field Strength and Potential Difference
A stronger electric field produces greater acceleration between collisions, increasing the drift velocity. This relationship remains proportional for ohmic materials where resistance is constant.
4. Type and Temperature of Material
In metals, higher temperatures increase lattice vibrations, causing more collisions and reducing drift velocity for a given field.
In semiconductors, increasing temperature releases more charge carriers, increasing nnn and hence the overall current despite reduced individual drift speeds.
The Physical Picture of Drift
To visualise drift velocity, imagine each electron repeatedly accelerating between collisions with stationary ions in a lattice. Each collision randomises its direction, but the overall motion remains slightly biased opposite to the electric field direction. The result is a net drift superimposed on rapid random motion.
This microscopic perspective clarifies why:
Electrical energy is transferred quickly through a conductor even though electrons move slowly.
Current remains steady in a circuit, as the number of electrons entering and leaving any cross-section per second remains constant.
Conservation of charge is maintained, linking microscopic electron movement to macroscopic circuit laws.
Summary of Conceptual Importance
Understanding mean drift velocity allows students to interpret how an apparently static solid metal wire can sustain continuous current flow. It bridges the gap between individual particle motion and measurable electrical quantities, forming a foundation for later study of current–voltage relationships, resistance, and conductivity.
FAQ
If the current doubles and the wire’s cross-sectional area and material remain unchanged, the mean drift velocity also doubles.
This is because drift velocity is directly proportional to current in the relation I = A n e v. Since A, n, and e are constant, doubling I means v must double to maintain equality.
The microscopic behaviour of electrons changes only slightly — collisions still occur frequently, but the net bias of motion becomes stronger.
Although electrical signals and energy transmission happen almost instantaneously, individual electrons move very slowly.
The number density (n) of free electrons in metals is extremely large (around 10²⁸ m⁻³).
As a result, even a tiny drift velocity corresponds to a substantial total current.
Typical drift velocities in household wiring are on the order of millimetres per second, despite carrying several amperes of current.
Raising the temperature of a metal increases lattice vibrations, causing more frequent collisions between electrons and ions.
The average time between collisions (mean free time) decreases.
For a given electric field, this reduces the net acceleration and hence reduces the mean drift velocity.
Although drift velocity decreases, the number of charge carriers remains roughly constant in metals, so resistivity rises instead.
Yes — this occurs in semiconductors and electrolytes.
In semiconductors, both electrons (negative) and holes (positive) move and contribute to current
In electrolytes, positive ions drift one way and negative ions drift the other.
The total current is the algebraic sum of all carrier contributions. The overall direction of conventional current is defined as the direction of positive charge flow.
The electric signal — or the electromagnetic wave that drives the drift of electrons — travels at a significant fraction of the speed of light, not at the slow drift speed.
When a potential difference is applied, the electric field establishes almost instantly throughout the conductor, causing all electrons to begin drifting simultaneously.
Thus, while each electron drifts slowly, the effect of current flow appears to start everywhere in the wire almost at once.
Practice Questions
Question 1 (2 marks)
Explain what is meant by the term mean drift velocity of charge carriers in a conductor.
Mark Scheme:
1 mark: States that mean drift velocity is the average velocity of charge carriers when an electric field is applied.
1 mark: Mentions that it represents the net movement of charge carriers superimposed on their random thermal motion.
Question 2 (5 marks)
A metal wire carries a steady current. Describe, in terms of the motion of electrons, how the current arises in the wire.
In your answer you should:
explain what happens to the electrons when a potential difference is applied
describe how this leads to a net current
relate this motion to the concept of mean drift velocity
Mark Scheme:
1 mark: Recognises that free electrons in the metal move randomly due to thermal energy.
1 mark: States that applying a potential difference creates an electric field within the wire.
1 mark: Explains that the field exerts a force on the electrons, causing them to accelerate opposite to the field direction.
1 mark: Mentions that frequent collisions with lattice ions result in a small net average velocity — the mean drift velocity.
1 mark: States that the collective motion of many charge carriers with this mean drift velocity constitutes the electric current.

