AP Syllabus focus:
‘Recognize that polynomial, rational, power, exponential, logarithmic, and trigonometric functions are continuous at all points in their domains.’
Understanding which families of functions are automatically continuous allows students to analyze graphs and limits efficiently, knowing these functions behave smoothly wherever their domains permit evaluation.
Continuity of Common Function Families
Common function families provide the foundational building blocks for much of calculus. In AP Calculus AB, it is essential to recognize that many frequently used functions are continuous at every point in their domains, meaning they have no breaks, jumps, or holes wherever they are defined. This idea supports key limit techniques and prepares students for later differentiation rules, which rely heavily on continuity. A function is continuous on its domain if its graph can be drawn without lifting a pencil and if its limit at any domain point equals its function value there.
Continuity at a Point: A function is continuous at x = c if f(c) is defined, the limit of f(x) as x approaches c exists, and the limit equals the function value.
Polynomial, rational, power, exponential, logarithmic, and trigonometric functions all meet continuity conditions automatically on the sets of inputs for which they are defined. Each family has specific domain characteristics, and continuity is guaranteed at all those allowable points.
Polynomial Functions
Polynomial functions—expressions created using addition, subtraction, and multiplication of constants and powers of x—are among the simplest continuous functions.
Polynomial Function: A function formed by finite sums of constant multiples of nonnegative integer powers of x.
These functions are continuous everywhere on the real line.
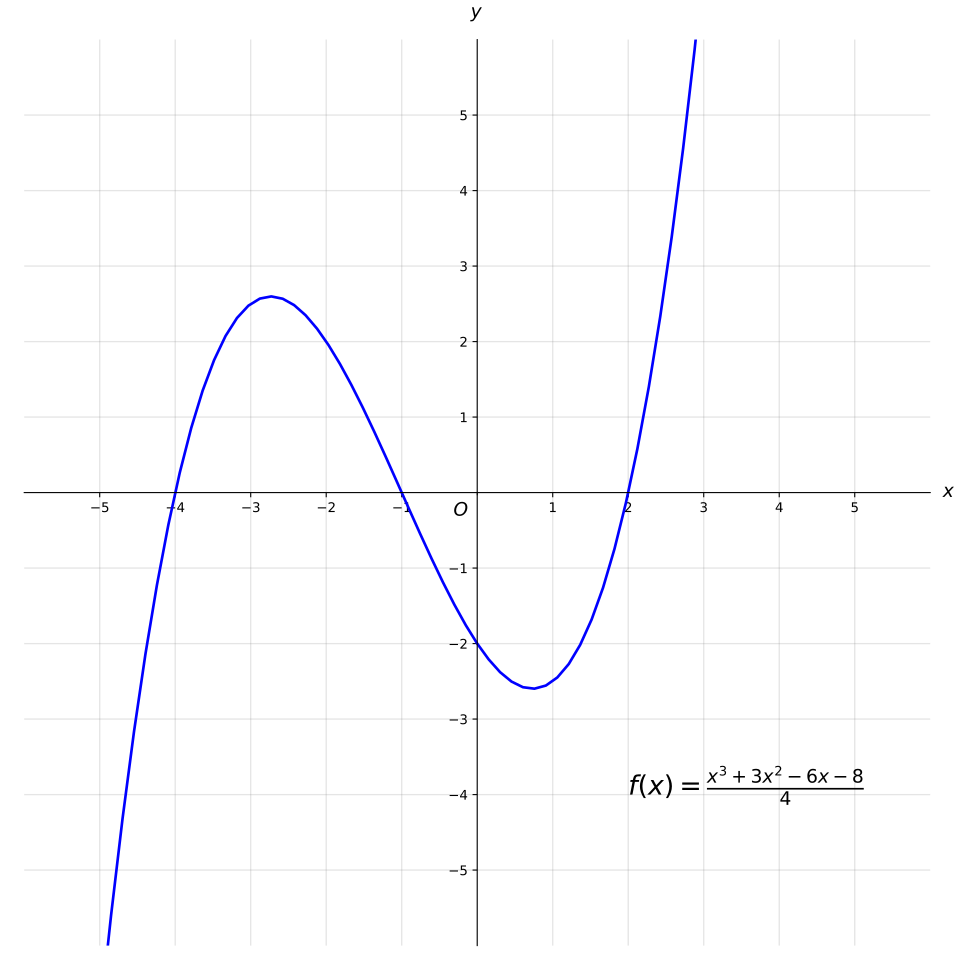
Graph of a cubic polynomial shown as a smooth, unbroken curve, illustrating that polynomial functions remain continuous for all real x with no gaps or discontinuities. Source.
Their graphs have no gaps, corners, or asymptotes, allowing limits to be evaluated by direct substitution. This makes polynomial families especially valuable for modeling real-world relationships.
Rational Functions
Rational functions are formed by the quotient of two polynomials. Their behavior is smooth except at points where the denominator equals zero.
Rational Function: A function of the form f(x) = P(x)/Q(x) where P and Q are polynomials and Q(x) is not equal to zero.
Rational functions are continuous everywhere their denominators do not vanish.
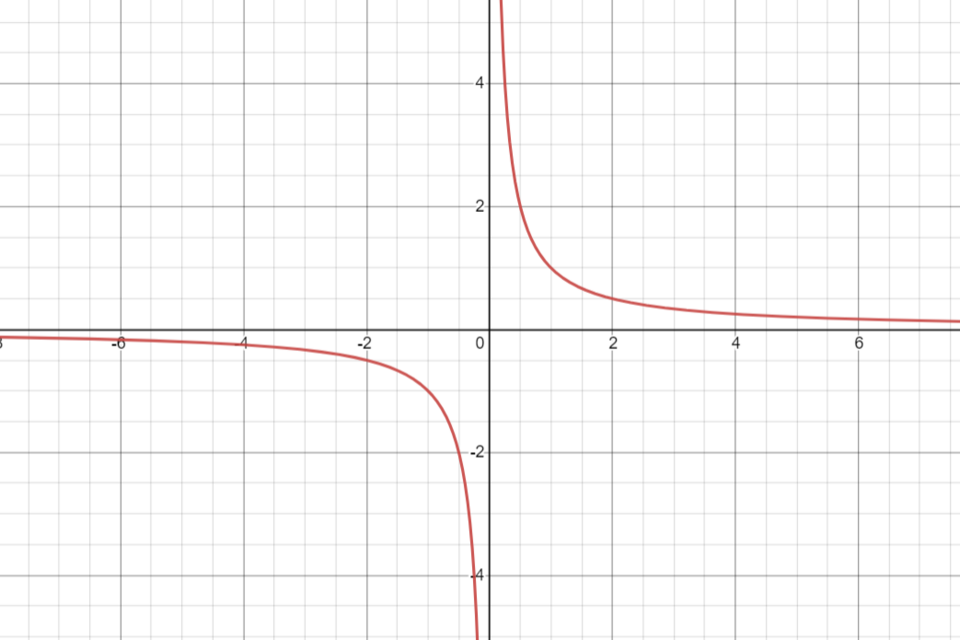
Graph of a rational function with smooth branches and visible domain restrictions, showing that continuity holds on all x-values where the denominator does not equal zero. Extra asymptotic detail reflects the natural behavior of rational functions but stays consistent with the topic. Source.
Points where Q(x) = 0 cause discontinuities, often vertical asymptotes or holes, but all other domain points exhibit uninterrupted continuity.
Key reminders about rational functions
Continuous on all x such that Q(x) is not zero
Discontinuities arise only from domain restrictions
Limits at allowed points can be computed using substitution or algebraic simplification
Power Functions
Power functions include expressions where x is raised to a real number exponent. They behave predictably and remain continuous wherever they are defined.
Power Function: A function of the form f(x) = x raised to the power a, where a is a real constant.
Depending on the exponent:
Even roots require x greater than or equal to 0
Odd roots allow all real x
Negative exponents require x not equal to 0
Within their valid domains, these functions have smooth curves with no jumps.
Exponential Functions
Exponential functions, in which a positive constant base is raised to a variable power, are continuous on all real numbers. Their steady growth or decay patterns support many limit evaluations.
Exponential Function: A function of the form f(x) = a raised to the x, where a is greater than 0 and not equal to 1.
Because a to the x never equals zero and never becomes undefined, its domain includes all real numbers, making it continuous everywhere.
Logarithmic Functions
Logarithmic functions are inverses of exponential functions. Their domain restrictions determine where they remain continuous.
Logarithmic Function: A function of the form f(x) = log base a of x, where a is greater than 0 and not equal to 1, defined only for x greater than 0.
Key continuity facts:
Continuous for all x greater than 0
Undefined at x less than or equal to 0
The smooth, slowly increasing graph reflects unbroken continuity in its domain
Trigonometric Functions
Trigonometric functions are continuous wherever they are defined, though some have domain gaps that produce discontinuities.
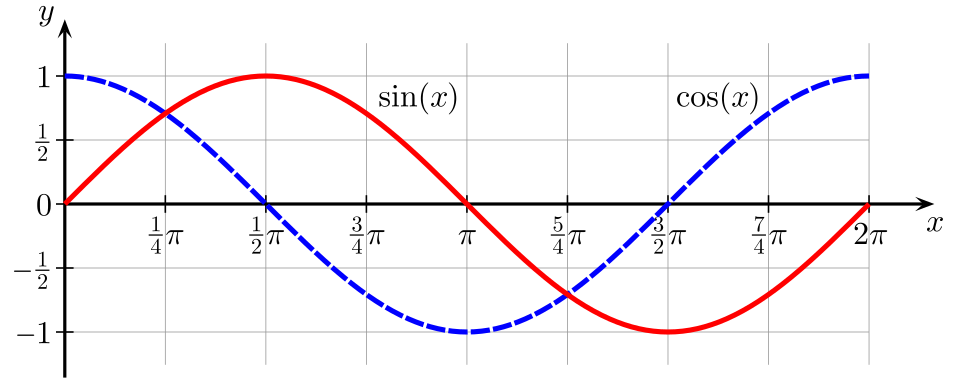
Plot of the functions y = sin(x) and y = cos(x) over one period, both drawn as smooth, continuous waves, illustrating that sine and cosine remain continuous for all real x. Periodic structure shown here adds contextual detail consistent with standard trigonometric understanding. Source.
Continuity characteristics
Sine and cosine: continuous for all real x
Tangent, secant, cotangent, cosecant: continuous except where their denominators are zero
For example, tangent is discontinuous at odd multiples of π/2
These functions exhibit predictable oscillatory patterns, and continuity on their domains ensures stable limit behavior.
Why Continuity of Function Families Matters
Recognizing the continuity of these families reduces the need for complex limit evaluation. When a function is continuous at a point in its domain:
The limit equals the function value
Direct substitution is valid and efficient
Algebraic manipulation becomes less necessary
Practical benefits for AP Calculus AB
Provides reliable tools for early limit evaluation
Supports understanding of differentiability rules
Allows for quick assessment of where discontinuities may or may not occur
The AP syllabus emphasizes knowing that these function families are continuous throughout their domains, making them essential foundations for all later calculus study.
FAQ
Most standard families have well-established continuity on their domains.
• Polynomials: always continuous everywhere.
• Exponential and trigonometric functions: continuous wherever defined.
• Logarithmic and rational functions: continuous on restricted domains only.
A fast check is to identify whether the function comes from these families and then look only for domain restrictions such as roots of denominators or non-positive logarithmic inputs.
Continuity is determined not only by a function’s algebraic structure but also by where the expression can be validly evaluated.
For rational and logarithmic functions, continuity fails precisely where the algebra makes the expression undefined.
• Denominator equal to zero creates a breach.
• Non-positive logarithmic inputs create invalid values.
Outside these restrictions, behaviour is smooth and therefore continuous.
Yes. A negative exponent introduces an implicit denominator, because x raised to a negative power is equivalent to 1 divided by x raised to a positive power.
This means:
• The function is continuous for all x except x = 0.
• The point of discontinuity comes solely from the domain restriction caused by division by zero.
Apart from this restriction, the curve behaves smoothly.
Periodicity does not alter continuity; it simply repeats continuous behaviour across intervals.
For sine and cosine, every repeated cycle is smooth and uninterrupted.
For tangent and the reciprocal trig functions, discontinuities reappear regularly at predictable intervals due to zeroes in the denominator.
Thus, periodicity helps identify where these breaks occur, but it does not cause them.
Fractional exponents can imply roots, and the type of root affects the allowable inputs.
• Even roots require non-negative inputs.
• Odd roots accept any real input.
When restricted by an even root, the function becomes continuous only on the interval where it is defined, typically x ≥ 0.
Outside this set, the function simply does not exist, and continuity cannot be applied.
Practice Questions
(1–3 marks)
A function g is defined by a rational expression. Explain why g must be continuous at every point where its denominator is non-zero. Give one specific reason linked to the structure of rational functions.
Question 1 (1–3 marks)
• 1 mark: States that rational functions are formed from the quotient of two polynomials.
• 1 mark: States that polynomials are continuous for all real numbers.
• 1 mark: Concludes that the rational function is continuous wherever the denominator is non-zero because the quotient of continuous functions is continuous on its domain.
Total: 3 marks.
(4–6 marks)
Consider the function h defined by
h(x) = x^3 + 2x for all real x,
and the function k defined by
k(x) = log(x − 1) for x > 1.
(a) State the domain on which h is continuous and justify your answer.
(b) State the domain on which k is continuous and justify your answer.
(c) Use your answers to parts (a) and (b) to determine all x-values for which the composite function h(k(x)) is continuous. Clearly justify your reasoning.
Question 2 (4–6 marks)
(a)
• 1 mark: States that h(x) is continuous for all real x.
• 1 mark: Justifies this by noting that polynomials are continuous everywhere.
(b)
• 1 mark: States that k(x) is continuous for x > 1.
• 1 mark: Justifies this by noting that logarithmic functions are continuous on their domains, which require the argument to be positive.
(c)
• 1 mark: Identifies that h(k(x)) is defined only when k(x) is defined, i.e. x > 1.
• 1 mark: States that the composite is continuous for x > 1 because composition of continuous functions is continuous on the domain where both inner and outer functions are continuous.
Total: 6 marks.

