AP Syllabus focus:
‘Use properties that sums, differences, products, quotients, and compositions of continuous functions are also continuous on appropriate domains.'
These notes explain how continuity is preserved when combining functions algebraically, emphasizing domain restrictions and interval types to ensure valid conclusions in AP Calculus AB.
Continuity and Algebraic Combinations
In AP Calculus AB, continuity is not only a property of individual functions but also a property that can be preserved under algebraic operations. This allows students to analyze complex functions efficiently without rechecking continuity from first principles. When functions are combined through standard algebraic operations, their continuity depends on both the continuity of each component function and the domain on which the combination is defined.
The AP syllabus emphasizes that continuity is maintained when using sums, differences, products, quotients, and compositions, provided that all expressions involved are defined and behave appropriately on the interval under consideration.
Key Idea: Appropriate Domains
Before discussing specific algebraic rules, it is essential to understand the phrase “appropriate domains.” Continuity statements are always tied to where a function is defined.
Appropriate domain: The set of all x-values for which a function or algebraic combination of functions is defined and free of operations that cause undefined behavior.
A combined function can only be continuous on the part of the domain where every component function is continuous and every algebraic operation is valid. Domain restrictions often arise from division by zero, even if the original functions are continuous everywhere else.
Always consider:
Where each original function is defined
Where the algebraic operation itself is valid
How interval endpoints affect continuity claims
Sums and Differences of Continuous Functions
If two functions are continuous on an interval, their sum and difference are also continuous on that same interval. This rule applies equally to open, closed, and half-open intervals, provided both functions are continuous at every interior point and, when relevant, at the endpoints.
Important features of this rule include:
No new restrictions are introduced by addition or subtraction
Continuity is preserved point-by-point across the shared domain
Interval type matters only in terms of where continuity must be checked
Because of this property, expressions formed by adding or subtracting polynomials, exponentials, logarithms, or trigonometric functions remain continuous wherever all components are defined.
Products of Continuous Functions
The product of two continuous functions is continuous on any interval where both functions are continuous. Like sums and differences, multiplication does not introduce new domain restrictions.
Key points to remember:
Zeros in either function do not disrupt continuity
Products remain continuous even when function values change sign
Interval endpoints follow the same continuity requirements as interior points
This rule allows complex expressions involving multiple multiplied functions to be treated as continuous without additional verification.
Quotients and Domain Restrictions
The quotient of two continuous functions is continuous only where the denominator is nonzero.
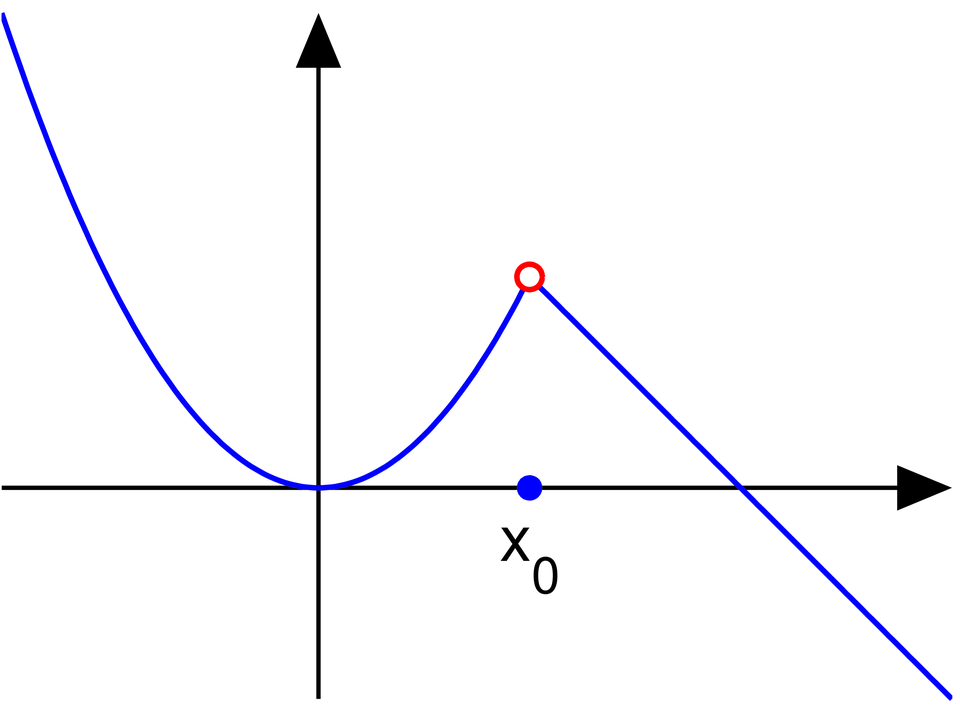
The graph illustrates a function that approaches a single y-value but is undefined at that x-value due to a hole. This highlights that quotients are continuous only where the denominator is nonzero, even if nearby behavior appears smooth. Source.
For quotients:
Both numerator and denominator must be continuous
The denominator must not equal zero on the interval
Any x-value that makes the denominator zero must be excluded from continuity claims
This restriction often leads to holes or vertical asymptotes, which prevent continuity even if the original functions are continuous everywhere else.
Compositions of Continuous Functions
A composition of functions is continuous when the outer function is continuous at the output values of the inner function, and the inner function is continuous on its domain.
If g is continuous at c and f is continuous at g(c), then the composite function f∘g is continuous at c.
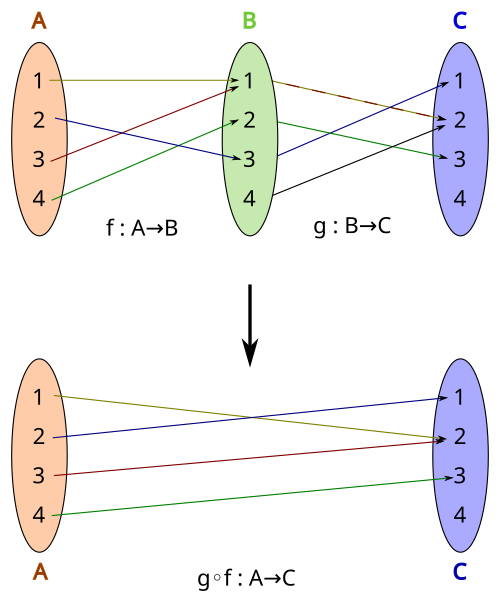
This diagram shows composition as a two-step process: inputs are first mapped by g, then the outputs are mapped by f. The combined arrows represent the composite function f∘g, clarifying how continuity depends on both functions. Source.
This rule requires careful attention to how functions interact:
The inner function determines which values are fed into the outer function
The outer function must be continuous for all those resulting values
Domain restrictions from either function apply to the composition
Compositions are especially common when working with nested expressions, such as trigonometric functions inside polynomials or logarithms of rational expressions.
Continuity on Different Types of Intervals
Algebraic rules for continuity apply uniformly across open, closed, and half-open intervals, but the interpretation differs slightly:
On open intervals, continuity is required only at interior points
On closed intervals, continuity must include both endpoints
On half-open intervals, continuity applies only where the function is defined
When combining functions, always match the continuity requirements to the interval type. A function may be continuous on an open interval but fail to be continuous on a closed interval if it is undefined or discontinuous at an endpoint.
Why These Rules Matter
Using algebraic rules for combining continuous functions allows students to:
Make fast, reliable continuity claims
Focus on domain analysis instead of repeated limit checking
Prepare for advanced applications like the Intermediate Value Theorem
These properties form a foundational toolkit for analyzing increasingly complex functions throughout AP Calculus AB.
FAQ
Continuity depends on how a function is built, not how complex it appears.
If a function is formed using sums, products, quotients (with nonzero denominators), or compositions of continuous functions, continuity is preserved automatically.
This means a long or nested expression can still be continuous everywhere in its domain without checking limits at each point.
Continuity can only be claimed where the function is defined.
If a denominator becomes zero or an expression is undefined at an endpoint, continuity on a closed interval fails, even if the function is continuous everywhere else.
Always check whether the entire interval lies within the function’s domain before stating continuity.
Yes, but only through domain restrictions.
Discontinuities arise when:
A denominator equals zero
A composed function inputs values outside the outer function’s domain
Algebraic operations themselves do not cause discontinuities; invalid inputs do.
A combined function is only defined where all component functions are defined.
Continuity is guaranteed only on this shared region.
Ignoring domain overlap can lead to incorrect conclusions about continuity, especially when functions are defined on different types of intervals.
No.
Continuity on a closed interval requires continuity at the endpoints as well.
If a function is undefined or discontinuous at an endpoint, it may be continuous on the open interval but not on the corresponding closed interval.
Practice Questions
Question 1 (2 marks)
Functions f and g are continuous on the interval [−2, 3].
The function h is defined by h(x) = f(x) + g(x).
State whether h is continuous on [−2, 3] and justify your answer.
Question 1 (2 marks total)
1 mark: Correctly states that h is continuous on [−2, 3].
1 mark: Justification that the sum of two functions continuous on an interval is also continuous on that interval.
Question 2 (5 marks)
The functions f and g are defined as follows:
f is continuous on the interval [0, 4].
g is continuous on the interval (−2, 2) and g(x) ≠ 0 for all x in this interval.
A new function h is defined by h(x) = f(x) / g(x).
(a) State the largest interval on which h is guaranteed to be continuous.
(b) Explain why h is not guaranteed to be continuous at x = 2.
(c) Suppose g is also continuous at x = 2 and g(2) ≠ 0. State whether h would then be continuous at x = 2 and justify your answer.
Question 2 (5 marks total)
(a) Largest interval of continuity (2 marks)
1 mark: Identifies the interval as (0, 2).
1 mark: Justifies using the overlap of the domains of continuity of f and g.
(b) Continuity at x = 2 (1 mark)
1 mark: Correct explanation that g is not known to be continuous at x = 2, so the quotient rule for continuity cannot be applied there.
(c) Extended condition at x = 2 (2 marks)
1 mark: Correctly states that h would be continuous at x = 2.
1 mark: Justification that both f and g are continuous at x = 2 and g(2) ≠ 0, so their quotient is continuous at that point.

